9 Covariance and Correlation

9.1 Preliminary Note

In this chapter, we briefly return to probability calculus and define the concept of covariance of random variables. This will enable us to assess the variability of linear combinations of random variables when they are not independent, but rather exhibit a specific type of coupling known as correlation. The case of independence has already been thoroughly discussed in Chapter 5.

We will link the concept of covariance with the ideas developed in Chapter 8 regarding optimization under constraints to eventually discuss an extraordinarily exciting topic from modern financial mathematics, the optimization of a portfolio. We have already encountered this problem in Section 5.3.5, though at that time we were limited to financial investments with independent random return variables.

9.2 The Covariance of Random Variables

Let \(X\) and \(Y\) be two random variables with the expected values \(\mu_x,\,\mu_y\) and the variances \(\sigma_x^2,\,\sigma_y^2\). We now want to calculate the expected value and the variance of a linear combination \(aX+bY\).

From Theorem 5.40 we know that \[ \begin{gathered} E(aX+bY)=aE(X)+bE(Y). \end{gathered} \] This formula is always correct (as long as the expected values exist). In the case of variance, the matter is not as simple. From Theorem 5.56, we know that for independent random variables the formula \[ \begin{gathered} V(aX+bY)=a^2V(X)+b^2V(Y) \end{gathered} \] applies. Now the question arises as to how to calculate the variance of a linear combination when the random variables are not independent. To answer this question, we need a new term.

Definition 9.1 The covariance of two random variables \(X\) and \(Y\) is defined as \[ \begin{gathered} \Cov(X,Y)=\sigma_{xy}=E((X-\mu_x)(Y-\mu_y)). \end{gathered} \]

At first, covariance is just a shorthand for the term that appears when calculating the variance of a sum of random variables (see the justification of Theorem 5.56): \[ \begin{gathered} V(X+Y)=V(X)+2\Cov(X,Y)+V(Y)= \sigma_x^2+2\sigma_{xy}+\sigma_y^2. \end{gathered} \tag{9.1}\] However, covariance also has its own independent meaning.

Covariance is closely related to the concept of variance. It is obvious that \(\Cov(X,X)=V(X)\): The covariance of a random variable with itself is identical to the variance of the random variable.

Another property that covariance shares with variance is that if one of the two random variables is constant, then the covariance equals zero. This is easy to understand. If \(X\) is constant, then \(X=\mu_x\) and therefore \(X-\mu_x=0\). Consequently, \[ \begin{gathered} \Cov(X,Y)=E(0\cdot(Y-\mu_y))=E(0)=0. \end{gathered} \]

Particularly important for what follows is the following fact.

Theorem 9.2 If the two random variables \(X\) and \(Y\) are stochastically independent, then the covariance of \(X\) and \(Y\) is equal to zero, that is \(\Cov(X,Y)=0\).

Justification: From the multiplication rule for expected values (Theorem 5.48), we know that the expected value of the product of independent random variables is equal to the product of the expected values. Thus, \[ \begin{gathered} \Cov(X,Y)=E((X-\mu_x)(Y-\mu_y))=E(X-\mu_x)E(Y-\mu_y) \end{gathered} \] Each of the two factors is zero because \[ \begin{gathered} E(X-\mu_x)=E(X)-\mu_x=0,\quad E(Y-\mu_y)=E(Y)-\mu_y=0, \end{gathered} \] and therefore \(\Cov(X,Y)=0\). □

If the covariance is not zero, it means that the random variables are coupled.

The covariance is a measure for a certain type of coupling of random variables. This kind of coupling is called correlation.

Remark 9.3 (Interpretation of Correlation) To understand what correlation means, one must understand the product \[ \begin{gathered} (X-\mu_x)(Y-\mu_y) \end{gathered} \] This product is positive when either both factors are positive or both are negative. However, this means that both random variables take on a value that is above-average (\(X>\mu_x\) and \(Y>\mu_y\)) or below-average (\(X<\mu_x\) and \(Y<\mu_y\)) at the same time. The product is negative when exactly one of the factors is negative, so when \(X\) is above-average and \(Y\) is below-average (\(X>\mu_x\) and \(Y<\mu_y\)), or vice versa.

If \(\Cov(X,Y)>0\) (positive correlation), then the realizations, where \(X\) and \(Y\) deviate from their expected value in the same direction (with regard to frequency and magnitude), predominate.

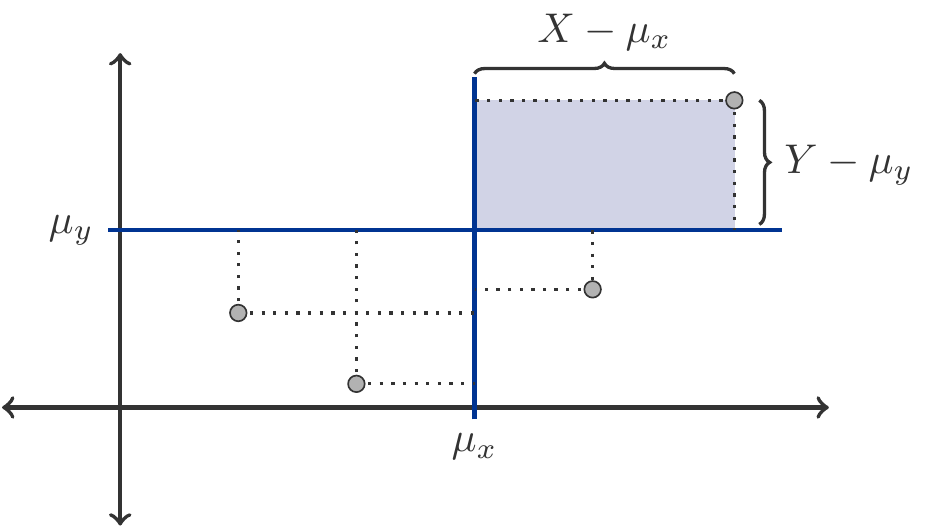
This situation is illustrated in Figure 9.1. The products \((X-\mu_x)(Y-\mu_y)\) are nothing but the area contents (with sign) of the rectangles defined by the points \((X,Y)\) and \(\mu_x,\mu_y\).

In the case of positive correlation, the pairs of values \((X,Y)\) are predominantly located in the first or third quadrants with respect to their common center of gravity \((\mu_x,\mu_y)\). The rectangles in these quadrants have positive content.

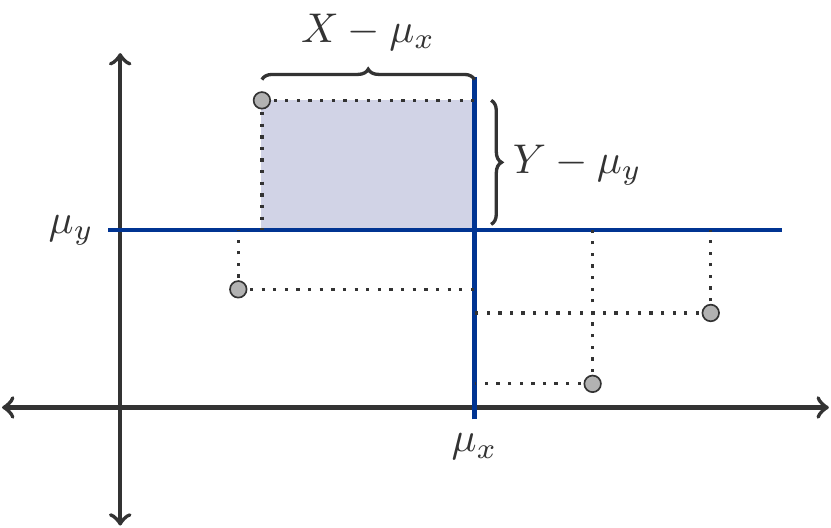
However, if \(\Cov(X,Y)<0\) (negative correlation), then realizations where \(X\) and \(Y\) deviate in different directions from their expected value (with regard to frequency and magnitude) predominate.

Therefore, with negative correlation, the pairs of values \((X,Y)\) are predominantly located in the second or fourth quadrants with respect to their common center of gravity \((\mu_x,\mu_y)\). The rectangles in these quadrants have negative content, see Figure 9.2.

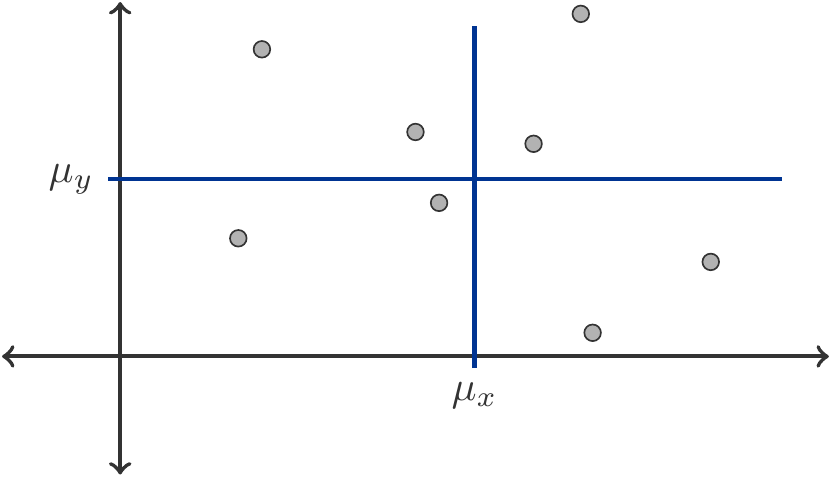
However, if \(X\) and \(Y\) are independent, then the value of \(Y\) is not affected by whether \(X\) takes above or below average values, \(\Cov(X,Y)=0\), see Figure 9.3. The pairs of values \((X,Y)\) are completely randomly distributed with respect to the common centroid \((\mu_x, \mu_y)\).

Figure 9.3: Uncorrelated Random Variables

Definition 9.4 Two random variables \(X, Y\) are called correlated if \(\Cov(X,Y)\not=0\). They are called positively correlated if \(\Cov(X,Y)>0\), and negatively correlated if \(\Cov(X,Y)<0\).

Exercise 9.5 Let \(X,Y\) be random variables with \(\sigma_x^2=3\), \(\sigma_y^2=5\) and \(V(X+Y)=9\). Calculate \(\sigma_{xy}\).

Solution: By using (9.1) \[ \begin{aligned} V(X+Y)&=\sigma_x^2+2\sigma_{xy}+\sigma_y^2\\[1ex] 9 &= 3+2\sigma_{xy}+5\\[2ex] \implies \sigma_{xy}&=1/2. \end{aligned} \] Thus, the two random variables are positively correlated. □

The covariance has several properties that are useful in computations. We summarize these properties concisely. Let \(X,Y\) and \(Z\) be random variables. The following hold:

Rule 1: \(\begin{array}{l} \Cov(X,X)=V(X) \end{array}\)

Rule 2: \(\begin{array}{l} \Cov(X,Y)=\Cov(Y,X) \end{array}\)

Rule 3: \(\begin{array}[t]{llcl} \Cov(X+Y,Z)&=\Cov(X,Z)&+&\Cov(Y,Z),\\ \Cov(X,Y+Z)&=\Cov(X,Y)&+&\Cov(X,Z) \end{array}\)

Rule 4: \(\begin{array}[t]{ll} \Cov(aX,Y)&=a\Cov(X,Y),\\ \Cov(X,bY)&=b\Cov(X,Y). \end{array}\)

It is not difficult to derive these properties from the definition of covariance and the properties of the expected value.

For the variance of a linear combination \(aX+bY\) of random variables, a general formula results.

Theorem 9.6 Let \(X\) and \(Y\) be random variables, then: \[ \begin{aligned} V(aX+bY)&=a^2V(X)+2ab\,\Cov(X,Y)+b^2V(Y)\\ &=a^2\sigma_x^2+2ab\sigma_{xy}+b^2\sigma_y^2. \end{aligned} \]

Justification: To justify, we set \(U=aX, W=bY\). Then, as we know, \[ \begin{gathered} V(aX+bY)=V(U+W)=V(U)+2\Cov(U,W)+V(W) \end{gathered} \] From the properties of variance, it follows that \(V(U)=a^2V(X)\) and \(V(W)=b^2V(Y)\). In addition, according to Rule 4: \[ \begin{gathered} \Cov(U,W)=\Cov(aX,bY)=ab\,\Cov(X,Y). \end{gathered} \] □

Exercise 9.7 Let \(X,Y\) be random variables with \(\sigma_x^2=3\), \(\sigma_y^2=5\) and \(\sigma_{xy}=-2\). Calculate \(V(X-2Y)\).

Solution: Using Theorem 9.6: \[ \begin{aligned} V(X-2Y)&=1^2\sigma_x^2-4\sigma_{xy}+4\sigma_y^2\\ &=1^2\cdot 3-4\cdot(-2)+4\cdot5=31. \end{aligned} \] □

Exercise 9.8 Let \(X,Y\) be random variables with \(\sigma_x^2=3\), \(\sigma_y^2=5\) and \(\sigma_{xy}=-2\).

Determine \(\Cov(X-2,Y+5)\).

Solution: We have \[ \begin{aligned} \Cov(X-2,Y+5)&=\Cov(X-2,Y)+\Cov(X-2,5). \end{aligned} \] The second term on the right is zero, because \(\Cov(c,X)=\Cov(X,c)=0\) when \(c\) is a constant. It follows that \[ \begin{aligned} \Cov(X-2,Y+5)&=\Cov(X-2,Y)\\[1ex] &=\Cov(X,Y)+\Cov(-2,Y) =\Cov(X,Y)=-2. \end{aligned} \] □

Exercise 9.9 Let \(X,Y\) be random variables with \(\sigma_x^2=3\), \(\sigma_y^2=5\) and \(\sigma_{xy}=-2\).

Determine \(\Cov(X+Y,2X)\).

Solution: \[ \begin{aligned} \Cov(X+Y,2X)&=\Cov(X,2X) +\Cov(Y,2X)\\[1ex] &=2\Cov(X,X)+2\Cov(Y,X)\\[1ex] &=2V(X)+2\Cov(X,Y)\\[1ex] &=2\cdot 3+2\cdot(-2)=2. \end{aligned} \] □

Exercise 9.10 Let \(X,Y\) be random variables with \(\sigma_x^2=3\), \(\sigma_y^2=5\) and \(\sigma_{xy}=-2\).

Determine \(\Cov(3X-Y,X+2Y)\).

Solution: \[ \begin{aligned} \Cov(3X-Y,&X+2Y)=\Cov(3X-Y,X) +2\Cov(3X-Y,Y)\\[1ex] &=3\Cov(X,X)-\Cov(Y,X)+6\Cov(X,Y) -2\Cov(Y,Y)\\[1ex] &=3\sigma_x^2+5\sigma_{xy}-2\sigma_y^2\\[1ex] &=9-10-10=-11. \end{aligned} \] □

Exercise 9.11 Let \(X,Y\) be random variables with \(\sigma_x^2=3\), \(\sigma_y^2=5\) and \(\sigma_{xy}=-2\).

Determine \(\Cov(X-5Y+3,7X-2)\).

Solution: \[ \begin{aligned} \Cov(X-5Y+3,7X-2)& =\Cov(X-5Y,7X)\\[1ex] & =\Cov(X,7X)-5\Cov(Y,7X)\\[1ex] & = 7V(X)-35\Cov(X,Y)\\[1ex] & = 21+70=91. \end{aligned} \] □

The next two exercises lead to our last topic.

Exercise 9.12 Let \(X,Y\) be the returns of two securities, with \(\sigma_x^2=0.2\), \(\sigma_y^2=0.3\) and \(\sigma_{xy}=-0.2\). Calculate the variance of the return of the portfolio that consists of 30 percent \(X\) and 70 percent \(Y\).

Solution: Let \(P=0.3X+0.7Y\) be the joint return of the portfolio. \[ \begin{gathered} V(0.3X+0.7Y)=0.3^2\cdot 0.2+2\cdot 0.3\cdot 0.7\cdot (-0.2) +0.7^2\cdot 0.3 =0.081\,. \end{gathered} \] □

Exercise 9.13 Let \(X,Y\) be the returns of two securities, with \(\sigma_x^2=0.2\), \(\sigma_y^2=0.3\) and \(\sigma_{xy}=-0.2\). Determine the portfolio whose return has the smallest variance. What is the variance of the return of the optimum portfolio?

Solution: Let \(\alpha\) and \(1-\alpha\) be the percentages of the capital invested in the two securities, respectively. The portfolio return \(P=\alpha X+(1-\alpha)Y\) has a variance \[ \begin{aligned} V(P)&=V(\alpha X+(1-\alpha)Y)\\ &=\alpha^2\cdot 0.2+2\alpha(1-\alpha)(-0.2)+(1-\alpha)^2\cdot 0.3\\ &=0.9\alpha^2-\alpha +0.3. \end{aligned} \] The variance is a quadratic function of \(\alpha\) and has its minimum at \(\alpha=0.5556\). Thus, the optimal portfolio is \((0.5556,0.4444)\). The variance is \(V(P)=0.0222\). □

9.3 Portfolio Optimization

The term portfolio was already discussed in detail in Section 5.3.5. Readers are invited to skim these pages again for orientation to more easily follow the discussions here.

The crucial ideas summarized in brief:

A portfolio is a decision about the percentage allocation of available capital to two or more securities.
The returns of these securities are usually random variables with a variance.
The variance of the joint return is considered a measure of the capital risk associated with the portfolio.
The greater the variance of the joint return, the riskier the investment.

Therefore, it is natural to turn the capital shares of the securities in the portfolio into decision variables of an optimization problem.

In solving this optimization task, we restrict ourselves to portfolios made up of a maximum of three securities. This limitation is for practical reasons and can be relaxed with a little more effort.

An investor has the option to invest his capital either in fixed-interest securities with a guaranteed interest rate \(r\), or in one or both of two other securities. The investor forms a portfolio from these three securities, wherein he invests the percentages \(\alpha_0\), \(\alpha_1\), and \(\alpha_2\) of his available capital.

Let \(X_0\), \(X_1\), and \(X_2\) be the returns (for a period) of the three securities. The expected values and variances of the returns are \[ \begin{gathered} \begin{array}{l@{\quad}l} E(X_0)=r& V(X_0)=0,\\ E(X_1)=\mu_1 & V(X_1)=\sigma_1^2,\\ E(X_2)=\mu_2 & V(X_2)=\sigma_2^2. \end{array} \end{gathered} \] The covariance is \(\Cov(X_1,X_2)=\sigma_{12}\). The covariances of \(X_0\) with \(X_1\) and \(X_2\) are zero because \(X_0\) is a constant.

A portfolio is defined by three numbers \(\alpha_0\), \(\alpha_1\) and \(\alpha_2\) with the property \[ \begin{gathered} \alpha_0+\alpha_1+\alpha_2=1. \end{gathered} \] These three numbers correspond to the percentages by which the investor’s available starting capital is allocated to the three securities. They are the capital shares of the securities in the portfolio.

Remark 9.14 (A Selection Problem) It is important to point out the following aspects separately:

We assume that in the portfolios we consider, a certain portion of the capital can be invested in fixed-income and thus risk-free. Risk-free means that the variance of the return of this investment is zero.
The decision on what the other two papers of the portfolio are, has already been made. Investors have therefore sufficiently informed themselves and decided which papers they will invest in.
Our task will be to determine the optimal capital shares \(\alpha_0,\alpha_1\) and \(\alpha_2\).

The mentioned selection problem is not easy to solve. Undoubtedly, however, the covariance of the returns of the papers will play a role. If \(\Cov(X_1,X_2)>0\), it stands behind quite a risk-prone strategy because if \(X_1\) increases, then \(X_2\) also tends to increase. But this also applies in the reverse direction: a deterioration in \(X_1\) is generally accompanied by a weakening of \(X_2\). The typical example would be to invest in stocks of a car manufacturer and in those of an automotive supplier.

Conversely, if the two non fixed-income papers are selected such that \(\Cov(X_1,X_2)<0\), then it expresses a more defensive strategy. Negative covariance of the returns means that the returns tend to move in opposite directions. A weakening in \(X_1\) is compensated by a strengthening of \(X_2\) and vice versa. For example, one could invest in coal power plant operators and alternatively in companies that provide energy from renewable sources.

Remark 9.15 (Negative Capital Shares) The percentages that define a portfolio can also be negative! A negative percentage means that the investor borrows capital at the beginning of the period and must pay it back at the end of the period, including the return of the corresponding security. In other words, one deliberately makes a liability a part of the portfolio.

The investor’s starting capital is \(K\).

If the portfolio is defined by \((-0.2,0.6,0.6)\), it means that the investor borrows an additional \(0.2K\) at a fixed interest rate \(r\) as a loan and uses it to finance securities 1 and 2, each valued at \(0.6K\). Part of his portfolio is therefore the liability to repay the amount of \(0.2K(1+r)\) at the end.

Thus, the investor commits to deliver a savings book with a credit balance of \(0.2K(1+r)\) at the end of the period and receives the amount of \(0.2K\) at the beginning of the period as a price for this commitment. This process is called Short Selling.

If the portfolio is defined by \((0.6,-0.2,0.6)\), it means that the investor raises the amount of \(0.2K\) by committing to deliver the amount of \(0.2K(1+X_1)\) at the end of the period (effectively delivering security 1 to this extent). The investor could, for example, borrow securities at the daily rate of \(0.2K\) at the beginning of the period and sell them on the stock exchange. At the end of the period, these securities must be repurchased on the stock exchange at the current rate of \(0.2K(1+X_1)\).

Short selling is sensible when the additional capital raised in this way can be invested better than the costs incurred by the liability.

The return of the portfolio is the random variable \[ \begin{aligned} P&=\alpha_0 r+\alpha_1 X_1+ \alpha_2 X_2\\ &=(1-\alpha_1-\alpha_2)r+\alpha_1 X_1+ \alpha_2 X_2\\ &=r+\alpha_1(X_1-r)+\alpha_2(X_2-r). \end{aligned} \]

We now calculate the expected value and variance of the portfolio return. The expected value of the portfolio’s return is \[ \begin{gathered} E(P)=r+\alpha_1(\mu_1-r)+\alpha_2(\mu_2-r). \end{gathered} \] The differences \(\mu_1-r\) and \(\mu_2-r\) are also called the risk premiums of the two securities.

We calculate the variance of the return with the help of Theorem 9.6: \[ \begin{gathered} V(P)=\alpha_1^2\sigma_1^2+2\alpha_1\alpha_2\sigma_{12}+ \alpha_2^2\sigma_2^2. \end{gathered} \] The investor is interested in choosing their portfolio, meaning the percentages \(\alpha_1\) and \(\alpha_2\), so as to achieve the highest possible return (expected value) with the least possible risk (variance). However, these two investment objectives are in competition with each other, so an appropriate compromise must be found.

Two possible strategies are:

Minimize risk subject to a given expected return - the defensive strategy.
Maximize the expected return subject to a given risk - the offensive strategy.

Both tasks lead to an optimization problem with constraints, which we can solve with the Lagrange Method (see Section 8.8.2).

Of course, there are all possible intermediate forms between these two variants, depending on the risk affinity of the investors.

Risk Minimization

Exercise 9.16 An investor creates a portfolio consisting of three securities, the first of which is fixed-interest with a rate of 7 percent. The other two securities have returns with expected values of 0.08 and 0.12, and variances of 0.04 and 0.09. The covariance of the returns of the two securities is 0.036.

The investor wants a portfolio with an expected return of 0.1 and minimal variance.

How should the investor allocate the starting capital across the three securities?
What is the variance of the return of the optimal portfolio?

Solution: The objective function to be minimized is the variance of the portfolio, which is defined as \[ \begin{gathered} C(\alpha_1,\alpha_2)=V(P)=0.04\alpha_1^2+0.072\alpha_1\alpha_2+ 0.09\alpha_2^2\to\min. \end{gathered} \] The constraint stipulates that the expected return of the portfolio must be \(0.1\). This means \[ \begin{aligned} F(\alpha_1,\alpha_2)&=E(P)\\ &=0.07+\alpha_1(0.08-0.07)+\alpha_2(0.12-0.07)=0.1, \end{aligned} \] or simplified \[ \begin{gathered} 0.01\alpha_1+0.05\alpha_2=0.03\,.\qquad \mbox{(A)} \end{gathered} \] Subject to this constraint, the objective function is to be minimized. We apply the method of Lagrange multipliers. The Lagrange function is given by \[ \begin{gathered} \begin{array}{rcl} L(\alpha_1,\alpha_2)&=&C(\alpha_1,\alpha_2)-\lambda(F(\alpha_1,\alpha_2)-0.1)\\ &=&0.04\alpha_1^2+0.072\alpha_1\alpha_2+0.09\alpha_2^2\\ & &-\lambda(0.01\alpha_1+0.05\alpha_2-0.03). \end{array} \end{gathered} \] To find a critical point, we calculate the partial derivatives and set them to zero: \[ \begin{gathered} \begin{array}{rcrcrcrcc} L_1'&=&0.080\alpha_1&+&0.072\alpha_2&-&0.01\lambda&=&0\\ L_2'&=&0.072\alpha_1&+&0.180\alpha_2&-&0.05\lambda&=&0 \end{array} \end{gathered} \] These equations lead to the solution \(\alpha_1=-0.1953\lambda\) and \(\alpha_2=0.3559\lambda\). Now we must choose \(\lambda\) such that the constraint is satisfied. For this purpose, we substitute the expressions for \(\alpha_1\) and \(\alpha_2\) into the constraint (A). This yields \[ \begin{gathered} \lambda=\frac{0.03}{-0.1953\cdot0.01+ 0.3559\cdot 0.05}=1.8937\,. \end{gathered} \] Therefore, the solution is \[ \begin{gathered} \alpha_1=-0.3698,\; \alpha_2=0.6740, \end{gathered} \] and the portfolio is given by \((0.6958,-0.3699,0.6740)\). We go short in security 1, the associated risk is the variance of this portfolio’s return \(V(P)=0.0284\). □

Remark 9.17 (Sensitivity of the Result) Readers will surely recall our economic interpretation of the Lagrange multiplier from Section 8.8.3. There we saw that \(\lambda\) represents the rate of change of the optimum with respect to the restriction set in the constraint.

In our example, \(\lambda\simeq 1.9\), the constraint in the constraint is the return goal \(q=0.1\). Suppose we increase the return goal to 11%. Then the value of the optimum of the objective function \(V^\ast(0.1)\), i.e., the risk, will increase. Approximately, this increase will be: \[ \begin{gathered} V^\ast(0.11)-V^\ast(0.1)\approx 0.01\cdot \lambda=0.019. \end{gathered} \] That means \[ \begin{gathered} V^\ast(0.11)\approx 0.0284+0.019=0.0474.\qquad \mbox{(D)} \end{gathered} \] Therefore, we expect a significant increase in investment risk!

Readers are invited to verify this forecast. Re-calculation with a return goal of 11% shows that the result is very sensitive. We now obtain a portfolio with a reduced risk-free portion \(\alpha_0\) and a significantly increased short position \(\alpha_1\) in paper 1. These additional funds go into security 2, whose capital share \(\alpha_2\) increases by 25%: \[ \begin{gathered} \alpha_0=0.5945,\quad \alpha_1=-0.4932, \quad \alpha_2=0.8987\,. \end{gathered} \] The variance of the return and thus the risk increase to \(V^\ast(0.11)=0.0505\). Prediction (D) is thus quite accurate.

Exercise 9.18 An investor compiles a portfolio of three securities, the first of which is a fixed-interest bond with an interest rate of 4 percent. The other two securities have expected returns of 0.06 and 0.1, and variances of 0.04 and 0.09. The covariance of the returns of the two securities is -0.018.

The investor wants to achieve a portfolio with an expected return of 0.08 and minimal variance.

How should the investor’s initial capital be allocated among the three securities?
What is the variance of the return of the optimal portfolio?

Solution: Let’s keep it shorter than in the previous example. The objective function, which we want to minimize, is \[ \begin{gathered} V(P)=0.04\alpha_1^2-0.036\alpha_1\alpha_2+ 0.09\alpha_2^2\to\min. \end{gathered} \] It should be minimized under the linear constraint \[ \begin{gathered} E(P)=0.04+\alpha_1(0.06-0.04)+\alpha_2(0.1-0.04)= 0.08, \end{gathered} \] i.e., \[ \begin{gathered} 0.02\alpha_1+0.06\alpha_2= 0.04, \end{gathered} \] minimized. The Lagrange function is \[ \begin{gathered} \begin{array}{rcl} L(\alpha_1,\alpha_2) &=& 0.04\alpha_1^2-0.036\alpha_1\alpha_2+0.09\alpha_2^2\\ &&-\lambda(0.02\alpha_1+0.06\alpha_2-0.04). \end{array} \end{gathered} \] The partial derivatives are set to zero: \[ \begin{aligned} \begin{array}{rcrcrcc} 0.080\alpha_1&-&0.036\alpha_2&-&0.02\lambda&=&0\\ -0.036\alpha_1&+&0.180\alpha_2&-&0.06\lambda&=&0 \end{array} \end{aligned} \]

These equations lead to the solution \(\alpha_1=0.4396\lambda\) and \(\alpha_2=0.4212\lambda\). Now, \(\lambda\) must be chosen such that the constraint is met. This leads to \[ \begin{gathered} \lambda=\frac{0.04}{0.4396\cdot0.02+ 0.4212\cdot 0.06}=1.1742\,. \end{gathered} \] Thus, the solution is \[ \begin{gathered} \alpha_1=0.5161,\; \alpha_2=0.4946\,. \end{gathered} \] and the portfolio is \((-0.0107,0.5161,0.4946)\). The variance of the return of this portfolio is \(V(P)=0.0235\). Now, we have short selling in the risk-free investment. The interpretation of the Lagrange multiplier is left to the readers. □

Return Maximization

Exercise 9.19 An investor composes a portfolio of three securities, of which the first is a fixed-income security with an interest rate of 7 percent. The other two securities have expected returns of 0.08 and 0.12, and the variances 0.04 and 0.09. The covariance of the returns of the two securities is -0.018.

The investor wants a portfolio with a variance of returns of 0.01 and maximum expected return.

How must the investor’s starting capital be allocated to the three securities?
What is the expected return of the optimal portfolio?

Solution: The objective function to be maximized is the expected return of the portfolio. It is given by \[ \begin{aligned} C(\alpha_1,\alpha_2)=E(P)&=0.07+\alpha_1(0.08-0.07)+\alpha_2 (0.12-0.07)\\ &=0.07+0.01\alpha_1+0.05\alpha_2. \end{aligned} \] The constraint states that the variance of the portfolio should be \(0.01\). This means \[ \begin{gathered} F(\alpha_1,\alpha_2)=V(P)=0.04\alpha_1^2 -0.036\alpha_1\alpha_2+ 0.09\alpha_2^2= 0.01\,. \end{gathered} \] Under this constraint, the objective function should be maximized. We apply the method of Lagrange multipliers. The Lagrange function is \[ \begin{gathered} \begin{array}{rcl} L(\alpha_1,\alpha_2)&=& C(\alpha_1,\alpha_2)-\lambda(F(\alpha_1,\alpha_2)-0.01)\\ &=& 0.07+0.01\alpha_1+0.05\alpha_2\\ &&-\lambda( 0.04\alpha_1^2 -0.036\alpha_1\alpha_2+ 0.09\alpha_2^2-0.01). \end{array} \end{gathered} \] To find a critical point, we form the partial derivatives and set these to zero: \[ \begin{gathered} \begin{array}{ccrcrcrcc} L_1'&=&0.01&-& 0.080\lambda\alpha_1 &+&0.036\lambda\alpha_2&=&0\\ L_2'&=&0.05 &+&0.036\lambda\alpha_1&-&0.180\lambda\alpha_2&=&0 \end{array} \end{gathered} \] These equations lead to the solution \(\alpha_1=0.2747/\lambda\) and \(\alpha_2=0.3327/\lambda\). Now \(\lambda\) must be chosen such that the constraint is met. For this purpose, we insert the expressions for \(\alpha_1\) and \(\alpha_2\) into the constraint. This results in \(\lambda^2=0.969\) and therefore \(\lambda_{1,2}=\pm \sqrt{0.969}=\pm 0.9845\).

We now have two critical points, depending on the sign of the multiplier. We also calculate the value of the objective function, the expected return: \[ \begin{gathered} \lambda_1=0.9845, \; \alpha_1=0.2791, \; \alpha_2=0.3380, \; C(\alpha_1,\alpha_2)=0.0897 \end{gathered} \] and \[ \begin{gathered} \lambda_2=-0.9845, \; \alpha_1=-0.2791, \; \alpha_2=-0.3380, \; C(\alpha_1,\alpha_2)=0.0503 \end{gathered} \] Since we are looking for the maximum expected return, we take the first of the two solutions, the one with the positive Lagrange multiplier. This yields an expected return of about 9% for a fixed-income capital share of \(\alpha_0=0.3829\).

By the way, we could have made the decision between \(\lambda_1\) and \(\lambda_2\) using a plausibility argument as well. Again, the economic interpretation of the Lagrange multiplier comes into play: if we increase the risk goal of \(0.01\), stipulated in the constraint, we also expect a higher average return in the optimum. Therefore, the optimal value of the multiplier must be positive. □

Exercise 9.20 An investor is assembling a portfolio consisting of three securities, of which the first is a fixed-income security with an interest rate of 3 percent. The other two securities have expected returns of 0.05 and 0.12, and variances of 0.04 and 0.07 respectively. The covariance of the returns of the two securities is 0.02115.

The investor wishes to create a portfolio with a variance of return of 0.02 and the highest possible expected return.

How should the investor’s initial capital be allocated among the three securities?
What is the expected return of the optimal portfolio?

Solution: The objective function to be minimized is \[ \begin{aligned} E(P)&=0.03+\alpha_1(0.05-0.03)+\alpha_2 (0.12-0.03)\\ &=0.03+0.02\alpha_1+0.09\alpha_2. \end{aligned} \] It should be maximized under the constraint \[ \begin{gathered} V(P)=0.04\alpha_1^2+ 0.0423\alpha_1\alpha_2+ 0.07\alpha_2^2= 0.02 \end{gathered} \] The Lagrange function is \[ \begin{gathered} \begin{array}{rcl} L(\alpha_1,\alpha_2)&=& 0.03+0.02\alpha_1+0.09\alpha_2\\ &&-\lambda( 0.04\alpha_1^2+ 0.0423\alpha_1\alpha_2+ 0.07\alpha_2^2-0.02) \end{array} \end{gathered} \] Forming the partial derivatives with respect to \(\alpha_1\) and \(\alpha_2\) yields the equations: \[ \begin{gathered} \begin{array}{rcrcrcc} 0.02&-&0.0800\lambda\alpha_1&-& 0.0423\lambda\alpha_2&=&0\\ 0.09&-& 0.0423\lambda\alpha_1&-&0.1400\lambda\alpha_2&=&0 \end{array} \end{gathered} \] These equations lead to the solution \(\alpha_1=-0.1070/\lambda\) and \(\alpha_2=0.6752/\lambda\). Now, \(\lambda\) must be chosen such that the constraint is satisfied. This leads to \(\lambda^2=1.4657\) or \(\lambda=\pm \sqrt{1.4657}\).

Once again we deal with two solutions, one of which is the maximum and the other the minimum. As outlined in the last example, only the positive value \(\lambda=\sqrt{1.4657}\) of the Lagrange multiplier can deliver the maximum. Therefore, we obtain the capital shares of the optimal portfolio as: \[ \begin{gathered} \alpha_0=0.5307,\quad \alpha_1=-0.0884,\quad \alpha_2=0.5577. \end{gathered} \] The optimal expected return amounts to \(0.0784\). □

9.4 Additional Exercises

Let \(X\) and \(Y\) be random variables with \(\sigma_x^2=20, \sigma_y^2=13\) and \(\sigma_{xy}=13\). Calculate \(V(9 X -3 Y)\).

Solution: \(V(9 X -3 Y)=1035\)
Let \(X\) and \(Y\) be random variables with \(\sigma_x^2=19, \sigma_y^2=18\) and \(V(9 X +8 Y)=4419\). Calculate \(\sigma_{xy}\).

Solution: \(\sigma_{xy}=12\)
Let \(X\) and \(Y\) be random variables with \(\sigma_x^2=18, \sigma_y^2=10\) and \(\sigma_{xy}=-11\). Calculate \(\Cov(X-14, Y+10)\).

Solution: \(\Cov(X-14,Y+10)=-11\)
Let \(X\) and \(Y\) be random variables with \(\sigma_x^2=13, \sigma_y^2=17\) and \(\sigma_{xy}=-12\). Calculate \(\Cov(X+Y,-10X)\).

Solution: \(\Cov(X+Y,-10X)=-10\)
Let \(X\) and \(Y\) be random variables with \(\sigma_x^2=11, \sigma_y^2=10\) and \(\sigma_{xy}=-7\). Calculate with these values \(\Cov(14X-Y,X+9Y)\).

Solution: \(\Cov(14X-Y,X+9Y)=-811\)
Let \(X\) and \(Y\) be the returns of two securities, with \(\sigma_x^2=0.1, \sigma_y^2=0.11\) and \(\sigma_{xy}=-0.07\). Calculate the variance of the return of a portfolio consisting of 67 percent of security 1 and 33 percent of security 2.

Solution: \(V(R)=0.0259\)
Let \(X\) and \(Y\) be the returns of two securities, with \(\sigma_x^2=0.34, \sigma_y^2=0.42\) and \(\sigma_{12}=0.28\). What is the percentage share of the securities in a portfolio whose return has the least variance?

Solution: 70%, 30%
An investor constructs a portfolio from three securities, of which the first has a fixed interest rate of \(5.5\) percent. The other two securities have expected returns of \(0.105\) and \(0.14\), and variances of \(0.06\) and \(0.09\). The covariance of the returns is \(0.04\). The investor wants a portfolio with an expected return of \(0.14\) and minimal variance. Calculate the capital shares of the optimal portfolio.

Solution: \(V=0.0862, \alpha_0=-0.1209,\alpha_1=0.2936,\alpha_2=0.8273\)
An investor constructs a portfolio from three securities, of which the first has a fixed interest rate of \(3\) percent. The other two securities have expected returns of \(0.125\) and \(0.09\), and variances of \(0.10\) and \(0.03\). The covariance of the returns is \(0.03\). An investor wants a portfolio with an expected return of \(0.10\) and minimal variance. What is the variance of the optimal portfolio?

Solution: \(V=0.0356, \alpha_0=-0.0182,\alpha_1= 0.2545,\alpha_2= 0.7636\)
An investor constructs a portfolio from three securities, of which the first has a fixed interest rate of \(7\) percent. The other two securities have expected returns of \(0.105\) and \(0.125\), and variances of \(0.05\) and \(0.04\). The covariance of the returns is \(0.03\). The investor wants a portfolio with a variance of \(0.02\) and the highest expected return. Calculate the capital shares of the optimum portfolio.

Solution: \(E(R)=0.1093, \alpha_0= 0.3284,\alpha_1= -0.1158,\alpha_2= 0.7874\)
An investor is compiling a portfolio consisting of three securities, of which the first is a fixed-income security with an interest rate of \(5\) percent. The other two securities have expected returns of \(0.12\) and \(0.09\), and variances of \(0.08\) and \(0.03\). The covariance of the returns is \(-0.03\). An investor wants a portfolio with a variance of \(0.015\) and maximum return. What is the expected return of the optimal portfolio?

Solution: \(E(R)=0.1166, \alpha_0= -0.2921,\alpha_1= 0.4958,\alpha_2= 0.7963\)