7 Matrices
\[ \definecolor{dgray}{rgb}{0.3,0.3,0.3} \definecolor{lgray}{rgb}{0.85,0.85,0.85} \]
7.1 Basic Concepts
7.1.1 Definitions
When numbers are arranged as a list, vectors are created. Sometimes, however, it is more advantageous to arrange a set of numbers two-dimensionally, i.e., in the form of a table in rows and columns. A rectangular number scheme of this kind is called a matrix. We have actually already encountered this term in the section 6.2 in connection with systems of linear equations.
Definition 7.1 A matrix is a rectangular array of numbers: \[ \begin{gathered} \mathbf A=(a_{ij})=\left(\begin{array}{rrcr} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array}\right). \end{gathered} \] If the matrix has \(m\) rows and \(n\) columns, then we say it is of the order \(m\times n\).
If the number of rows is equal to the number of columns (i.e., if \(m=n\)), then \(\mathbf A\) is called a square matrix.
It is customary to denote matrices with bold capital letters, e.g., \(\mathbf A, \mathbf X\), etc. If \(\mathbf A=(a_{ij})\) is a matrix, then \(a_{ij}\) denotes the component of the matrix in row \(i\) and column \(j\). The first index is always the row number and the second index is the column number. It doesn’t matter which letters we use for the indices.
The main diagonal of a matrix refers to the components with the same indices, i.e., \(a_{11},\,a_{22},\ldots\)
7.1.2 Special Matrices
We view vectors as special matrices. A column vector of dimension \(m\) is an \(m\times 1\) matrix and a row vector of dimension \(n\) is a \(1\times n\) matrix.
A matrix whose elements are all zero is called a zero matrix and denoted by \(\mathbf{0}\).
An important special matrix is the identity matrix. The identity matrix is denoted by \(\mathbf I\), it is a square matrix that contains the number \(1\) in the main diagonal and only zeros elsewhere: \[ \begin{gathered} \mathbf I=\left(\begin{array}{rrcr} 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \vdots &\vdots & \ddots &\vdots \\ 0 & 0 & \ldots & 1 \end{array} \right). \end{gathered} \tag{7.1}\]
7.1.3 Elementary Arithmetic Operations
One can perform arithmetic operations with matrices just like with vectors.
Addition of Matrices
Two matrices of the same order are added by adding the corresponding components: \[ \begin{aligned} \mathbf A+\mathbf B&=\left(\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots &\vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array}\right)+ \left(\begin{array}{cccc} b_{11} & b_{12} & \ldots & b_{1n} \\ b_{21} & b_{22} & \ldots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \ldots & b_{mn} \end{array}\right)\\[4pt] &= \left(\begin{array}{cccc} a_{11}+b_{11} & a_{12}+b_{12} & \ldots & a_{1n}+b_{1n} \\ a_{21}+b_{21} & a_{22}+b_{22} & \ldots & a_{2n}+b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}+b_{m1} & a_{m2}+b_{m2} & \ldots & a_{mn}+b_{mn} \end{array}\right) \end{aligned} \] The formation of the difference \(\mathbf A-\mathbf B\) is done in exactly the same way.
Multiplication of a Matrix by a Number
Matrices are multiplied by a number by multiplying all components by this number: \[ \begin{gathered} \gamma\mathbf A=\gamma\left(\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots &\vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array}\right)= \left(\begin{array}{cccc} \gamma a_{11} &\gamma a_{12} & \ldots & \gamma a_{1n}\\ \gamma a_{21} & \gamma a_{22} & \ldots & \gamma a_{2n} \\ \vdots &\vdots & \ddots &\vdots \\ \gamma a_{m1} & \gamma a_{m2} & \ldots & \gamma a_{mn} \end{array}\right) \end{gathered} \] So, the same rules of computation as for vectors apply.
Exercise 7.2 Consider the following matrices: \[ \begin{gathered} \small \mathbf A= \left(\begin{array}{rrr} 4 & 8 & -12\\ 12 & 16 & 8\\ 8 & -4 & 12 \end{array} \right), \mathbf B= \left(\begin{array}{rrr} 6 & 2& 10\\ 2 & -8& 14\\ 4 & 2& 6 \end{array} \right), \mathbf C= \left(\begin{array}{rrr} 1 & 0 & 2\\ 2 & 1 & 0\\ 0 & 0 & 2 \end{array} \right). \end{gathered} \]
Determine \(\mathbf X\) such that \(\mathbf A+\mathbf X=\mathbf B\).
Determine \(\mathbf X\) such that \(\frac{1}{2}(\mathbf A-2\mathbf X)+3\mathbf B=\mathbf X+6\mathbf C\).
Solution: To solve both equations, only elementary arithmetic operations are necessary, and with respect to these, matrices behave no differently than ordinary real numbers.
(a) We solve the equation formally for \(\mathbf X\) and then insert the numerical values. \[ \begin{gathered} \mathbf X=\mathbf B-\mathbf A=\left(\begin{array}{rrr} 2 & -6 & 22\\ -10 & -24 & 6\\ -4 & 6 & -6 \end{array}\right). \end{gathered} \] (b) \[ \begin{gathered} \mathbf X=\frac{1}{4}\mathbf A+\frac{3}{2}\mathbf B-3\mathbf C =\left( \begin{array}{rrr} 7 & 5 & 6\\ 0 & -11 & 23\\ 8 & 2 & 6 \end{array}\right). \end{gathered} \] □
Transposition of Matrices
An important arithmetic operation for matrices, which goes beyond what we are used to with numbers, is transposition. When transposing, the rows of a matrix are swapped with the columns.
Definition 7.3 Let \(\mathbf A\) be an \(m\times n\) matrix. The transposed matrix \(\mathbf A^\top\) is the \(n\times m\) matrix obtained from \(\mathbf A\) by swapping the rows and columns.
Of course, it holds that: \[ \begin{gathered} ({\mathbf A}^\top)^\top=\mathbf A \end{gathered} \tag{7.2}\]
If \(\displaystyle \mathbf A=\left(\begin{array}{rrrr} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{array}\right)\), then \(\displaystyle {\mathbf A}^\top=\left(\begin{array}{rrr} 1 & 5 & 9 \\ 2 & 6 & 10 \\ 3 & 7 & 11 \\ 4 & 8 & 12 \end{array}\right).\)
Through transposition, a column vector becomes a row vector and vice versa. For example, if \(\mathbf a\) is a column vector, then \({\mathbf a}^\top\) is a row vector: \[ \begin{gathered} \mathbf a=\left(\begin{array}{c} a_1\\a_2\\\vdots\\a_n \end{array}\right) \quad \Rightarrow \quad {\mathbf a}^\top=(a_1,a_2,\ldots,a_n). \end{gathered} \]
We now make an important agreement: whenever the term vector is used in the following, we mean column vector.
If we need row vectors, which will also occur, we create them by transposing a column vector.
Symmetric Matrices
For a square matrix, transposing is simply mirroring the matrix along its main diagonal (which is, as mentioned, the diagonal from the top left to the bottom right). A square matrix is called symmetric if it remains unchanged when mirrored along the main diagonal, that is, if it coincides with its transpose.
The matrix \(\mathbf A\) is symmetric. \[ \begin{gathered} \mathbf A=\left(\begin{array}{rrrr} 1 & 2 & 3 & 4 \\ 2 & 5 & 6 & 7 \\ 3 & 6 & 8 & 9\\ 4 & 7 & 9 &10 \end{array}\right)={\mathbf A}^\top \end{gathered} \]
Symmetric matrices will play an important role in the next chapter where we deal with calculus for functions of two variables.
7.2 Matrix Multiplication
Multiplication is a bit more difficult than the elementary arithmetic operations discussed earlier. It is possible to define a product of two matrices component-wise, provided that the factors involved are of the same order. But this kind of multiplication, the so-called Hadamard product1 is usually not meant when referring to matrix multiplication.
7.2.1 The Process of Matrix Multiplication
We start with a definition and then explain the process using an example.
Definition 7.6 The product of two matrices \(\mathbf A\) and \(\mathbf B\) results in a matrix \(\mathbf C=\mathbf A\cdot \mathbf B\), which is formed in the following way:
Multiply each row of \(\mathbf A\) with each column of \(\mathbf B\).
To multiply a row with a column means: Calculate the sum of the component products of the row and column.
The product of row \(i\) of \(\mathbf A\) with column \(j\) of \(\mathbf B\) yields the component \(c_{ij}\) of the result matrix \(\mathbf C\).
We now illustrate this definition with an example.
Given are the matrices \[ \begin{gathered} \mathbf A=\left(\begin{array}{ccc} 3 & 2 & 0\\ 2 & 4 & 1\\ 0 & 2 & 2\\ 4 & 1 & 0 \end{array}\right),\quad\mathbf B=\left(\begin{array}{cccc} 2 & 0 & 1 & 3\\ 1 & 2 & 1 & 0\\ 1 & 3 & 2 & 4 \end{array}\right). \end{gathered} \] Before we start with the calculation, let’s make an interesting observation: we will be able to form the product \(\mathbf A\cdot \mathbf B\), but it is not possible to compute \(\mathbf A+\mathbf B\) or \(\mathbf A-\mathbf B\) because the two matrices have different orders!
For the practical calculation, it is best to use a so-called Falk Scheme. This is a kind of rectangular coordinate system. In this, we fill in:
in the bottom left quadrant, the factor \(\mathbf A\);
in the top right quadrant, the factor \(\mathbf B\).
Afterwards, we sum the product of the components of each row of the left factor \(\mathbf A\) with each column of the right factor \(\mathbf B\) and write this sum in the bottom right quadrant: \[ \begin{gathered} \text{The Falk Scheme at the beginning of the calculation:}\quad \begin{array}{ccc|rrrr} & & & 2 & 0 & 1 & 3\\ & & & 1 & 2 & 1 & 0\\ & & & 1 & 3 & 2 & 4\\ \hline 3 & 2 & 0 & \\ 2 & 4 & 1 &\\ 0 & 2 & 2 &\\ 4 & 1 & 0 & \end{array} \end{gathered} \] Now we calculate: 1st row of \(\mathbf A\) \(\times\) 1st column of \(\mathbf B\): \[ \begin{gathered} \begin{array}{ccc|rrrr} & & & \cellcolor{lgray}2 & 0 & 1 & 3\\ & & & \cellcolor{lgray}1 & 2 & 1 & 0\\ & & & \cellcolor{lgray}1 & 3 & 2 & 4\\ \hline \cellcolor{lgray}3 & \cellcolor{lgray}2 & \cellcolor{lgray}0 & \cellcolor{dgray}{\color{white}\mathbf{8}}\\ 2 & 4 & 1 &\\ 0 & 2 & 2 &\\ 4 & 1 & 0 & \end{array}\qquad\begin{array}{ll} \text{Side calculation:}\\[5pt] 3\cdot 2+2\cdot 1+0\cdot 1=8 \end{array} \end{gathered} \] Now: 2nd row of \(\mathbf A\) \(\times\) 1st column of \(\mathbf B\): \[ \begin{gathered} \begin{array}{ccc|rrrr} & & & \cellcolor{lgray}2 & 0 & 1 & 3\\ & & & \cellcolor{lgray}1 & 2 & 1 & 0\\ & & & \cellcolor{lgray}1 & 3 & 2 & 4\\ \hline 3 & 2 & 0 & 8\\ \cellcolor{lgray}2 & \cellcolor{lgray}4 & \cellcolor{lgray}1 & \cellcolor{dgray}{\color{white}\mathbf{9}}\\ 0 & 2 & 2 &\\ 4 & 1 & 0 & \end{array}\qquad\begin{array}{ll} \text{Side calculation:}\\[5pt] 2\cdot 2+4\cdot 1+1\cdot 1=9 \end{array} \end{gathered} \] And so we continue and also multiply the 3rd and 4th row of \(\mathbf A\) with the first column of \(\mathbf B\). Once that is done, we repeat the process and multiply each row of \(\mathbf A\) with the 2nd column of \(\mathbf B\):
1st row of \(\mathbf A\) \(\times\) 2nd column of \(\mathbf B\): \[ \begin{gathered} \begin{array}{ccc|rrrr} & & & 2 & \cellcolor{lgray}0 & 1 & 3\\ & & & 1 & \cellcolor{lgray}2 & 1 & 0\\ & & & 1 & \cellcolor{lgray}3 & 2 & 4\\ \hline \cellcolor{lgray}3 & \cellcolor{lgray}2 & \cellcolor{lgray}0 & 8 & \cellcolor{dgray}{\color{white}\mathbf{4}}\\ 2 & 4 & 1 & 9\\ 0 & 2 & 2 & 4\\ 4 & 1 & 0 & 9 \end{array}\qquad\begin{array}{ll} \text{Side calculation:}\\[5pt] 3\cdot 0+2\cdot 2+0\cdot 3=4 \end{array} \end{gathered} \] If we continue this process until every row of \(\mathbf A\) has been multiplied with every column of \(\mathbf B\), then we will find the final product \(\mathbf C=\mathbf A\cdot \mathbf B\) in the bottom right quadrant of the Falk Scheme: \[ \begin{gathered} \begin{array}{ccc|rrrr} & & & 2 & 0 & 1 & 3\\ & & & 1 & 2 & 1 & 0\\ & & & 1 & 3 & 2 & 4\\ \hline 3 & 2 & 0 & 8 & 4 & 5 & 9\\ 2 & 4 & 1 & 9 & 11 & 8 & 10\\ 0 & 2 & 2 & 4 & 10 & 6 & 8\\ 4 & 1 & 0 & 9 & 2 & 5 & 12 \end{array},\qquad \mathbf C=\mathbf A\cdot \mathbf B=\left(\begin{array}{rrrr} 8 & 4 & 5 & 9\\ 9 & 11 & 8 & 10\\ 4 & 10 & 6 & 8\\ 9 & 2 & 5 & 12 \end{array} \right). \end{gathered} \]
The example shows that we can apparently only form the product if we are capable of making pairs from the components of the rows and columns of \(\mathbf A\) and \(\mathbf B\). Because these pairs need to be multiplied and then we must sum them up.
However, this is only possible if the rows of the left factor are as long as the columns of the right factor:
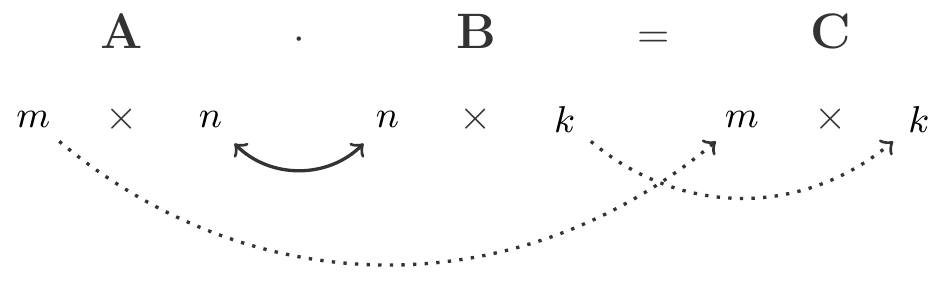
The resulting matrix \(\mathbf C\) inherits the number of rows from \(\mathbf A\) and the number of columns from \(\mathbf B\).
7.2.2 Properties of the Matrix Product
In Example 7.7 we had: \[ \begin{gathered} \begin{array}{ccccc} \mathbf A & \cdot & \mathbf B & = & \mathbf C \\ 4\times 3 & \leftrightarrow & 3\times 4 & & 4 \times 4 \end{array} \end{gathered} \] With the data from this example we can also calculate the product \(\mathbf B\cdot \mathbf A\). \[ \begin{gathered} \begin{array}{ccccc} \mathbf B & \cdot & \mathbf A & = & \mathbf D \\ 3\times 4 & \leftrightarrow & 4\times 3 & & 3 \times 3 \end{array} \end{gathered} \] The result, however, is a different matrix than \(\mathbf C\), namely: \[ \begin{gathered} \mathbf B\cdot \mathbf A=\mathbf D=\left(\begin{array}{rrr} 18 & 9 & 2\\ 7 & 12 & 4\\ 25 & 22 & 7 \end{array} \right) \end{gathered} \] Now it is clear that we must get a different result here. This is due to the way we form the product, which in this example results in \(\mathbf A\mathbf B\) and \(\mathbf B\mathbf A\) being of different order, and necessarily \(\mathbf A\mathbf B\ne \mathbf B\mathbf A\). But, what if we form the product of two square matrices of the same order?
If \(\mathbf A\) and \(\mathbf B\) are of the same order \(n\times n\), then \(\mathbf A\mathbf B\) and \(\mathbf B\mathbf A\) are also of the order \(n\times n\). Nevertheless, generally it still holds that: \(\mathbf A\mathbf B\ne \mathbf B\mathbf A\)!
Here’s an uncontroversial example: \[ \begin{gathered} \mathbf A=\left(\begin{array}{cc} 1& 2 \\3 & 4\end{array}\right),\qquad \mathbf B=\left(\begin{array}{rr}-5 & 2\\1 & 4\end{array}\right). \end{gathered} \] Please verify: \[ \begin{gathered} \mathbf A\mathbf B=\left(\begin{array}{rr} -3 & 10\\ -11 & 22 \end{array}\right),\qquad \mathbf B\mathbf A=\left(\begin{array}{rr} 1 & -2\\ 13 & 18 \end{array}\right) \end{gathered} \] We note this observation:
Theorem 7.8 The product of matrices is generally not commutative. That is, \[ \begin{gathered} \mathbf A\cdot \mathbf B\ne \mathbf B\cdot \mathbf A. \end{gathered} \]
The fact that the commutative law generally does not hold makes calculation with matrices somewhat more laborious.
However, there are exceptions to this rule. The most important exception is the identity matrix (see 7.1). It is the neutral element of matrix multiplication and it always holds that: \[ \begin{gathered} \mathbf A\cdot \mathbf I=\mathbf I\cdot \mathbf A=\mathbf A. \end{gathered} \tag{7.3}\] Mysteriously, however, for a given square matrix \(\mathbf A\) there are infinitely many other matrices that commute with \(\mathbf A\), which can’t easily be recognized from the outside. For example: \[ \begin{gathered} \mathbf A=\left(\begin{array}{cc} 1& 2 \\3 & 4\end{array}\right),\qquad \mathbf C=\left(\begin{array}{rr} 5 & 6\\ 9 & 14 \end{array}\right),\quad \mathbf A\mathbf C=\mathbf C\mathbf A= \left(\begin{array}{rr} 23 & 34\\ 51 & 74 \end{array}\right). \end{gathered} \] Apart from this peculiar oddity, the matrix product has properties that we reasonably expect from a product:
Theorem 7.9 (Associative Law) Let \(\mathbf A,\, \mathbf B\) and \(\mathbf C\) be matrices that are multiplicable with each other. Then \[ \begin{gathered} (\mathbf A\cdot \mathbf B)\cdot \mathbf C = \mathbf A\cdot (\mathbf B\cdot \mathbf C). \end{gathered} \tag{7.4}\]
This law states that the grouping (parenthesization) does not matter when multiplying more than two matrices. However, note that the order of the factors is not changed. It only determines which multiplication is performed first, which is second, and so on.
From the associative law follows that one can form powers of square matrices \(\mathbf A^2:=\mathbf A\cdot \mathbf A\), \(\mathbf A^3:=\mathbf A\cdot \mathbf A\cdot \mathbf A\), etc. If it were the case that \((\mathbf A\cdot \mathbf A)\cdot\mathbf A\not= \mathbf A\cdot(\mathbf A\cdot \mathbf A)\), then \(\mathbf A^3\) would be ambiguous and therefore undefined.
In addition, there is a distributive law, to be precise, there are even two of them. The reason that there are two is, of course, the absence of the commutative law.
Theorem 7.10 (Distributive Laws) If \(\mathbf A,\mathbf B,\mathbf C\) are matrices and the products \(\mathbf A\mathbf B, \mathbf A\mathbf C\) and \(\mathbf B\mathbf C\) are possible, then for the multiplication of the matrix \(\mathbf A\) from the left to the sum \(\mathbf B+\mathbf C\): \[ \begin{gathered} \mathbf A(\mathbf B+\mathbf C)=\mathbf A\mathbf B+\mathbf A\mathbf C. \end{gathered} \tag{7.5}\] Similarly, for multiplication from the right: \[ \begin{gathered} (\mathbf A+\mathbf B)\mathbf C=\mathbf A\mathbf C+\mathbf B\mathbf C. \end{gathered} \tag{7.6}\]
It is important to understand exactly what (7.5) states. Reading from left to right: we may resolve the parenthesis. Reading from right to left: we may factor out a common factor from two or more products. However, this factor must be on the same side in all products.
The following three exercises are not only intended for practice, they also show some more peculiar properties of the matrix product.
Exercise 7.11 Calculate the product \(\mathbf A\mathbf B\) with: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rrr} 1 & 3 & 2\\ 2 & 6 & 4\\ -3 & -9 & -6 \end{array}\right),\quad \mathbf B=\left(\begin{array}{rrr} -3 & -2 & -7\\ 1 & 0 & 1\\ 0 & 1 & 2 \end{array}\right). \end{gathered} \]
Solution: Using the Falk’s scheme, you find: \[ \begin{gathered} \mathbf A\mathbf B=\left(\begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right)=\mathbf{0} \end{gathered} \] □
This is another peculiar property of the matrix product. If for two real numbers \(a,b\) it holds that \(ab=0\), then we can be sure that one of the factors (or both) is zero. This rule does not apply to matrices anymore.
This has consequences when solving equations, a topic that we will soon discuss in more detail. When \(a,b\) and \(x\ne 0\) are real numbers, the well-known cancellation law applies: \[ \begin{gathered} ax=bx\implies a=b,\qquad\text{if }x\ne 0. \end{gathered} \] This rule generally does not apply to matrices.
Exercise 7.12 Calculate \(\mathbf A^2\), \(\mathbf A^3,\ldots\) of \[ \begin{gathered} \mathbf A=\left(\begin{array}{rrr}2 & 0 & -1\\1 & 1 & -1\\2 & 0 & -1 \end{array} \right). \end{gathered} \]
Solution: Using the Falk’s scheme, you find \(\mathbf A^2=\mathbf A\), but from this it follows that \(\mathbf A^n=\mathbf A\) for \(n=1,2,\ldots\). A matrix with this property is called idempotent. □
The following exercise also shows a peculiarity that we do not know from calculating with numbers.
Exercise 7.13 Calculate \(\mathbf A^2, \mathbf A^3,\ldots\) of \[ \begin{gathered} \mathbf A=\left(\begin{array}{rcc} -2 & 1 & 1\\ -3 & 1 & 2\\ -2 & 1 & 1 \end{array}\right). \end{gathered} \]
Solution: With a simple calculation, we find: \[ \begin{gathered} \mathbf A^2=\left(\begin{array}{rcc} -1 & 0 & 1\\ -1 & 0 & 1\\ -1 & 0 & 1 \end{array}\right), \quad \mathbf A^3=\left(\begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right). \end{gathered} \] Therefore, all powers \(\mathbf A^n, n\ge 3\) are equal to the zero matrix. A matrix with this property is called nilpotent. □
Here are more practice examples for matrix multiplication:
(a) \(\displaystyle \left(\begin{array}{rr} 1&2\\3&0\\0&4 \end{array}\right) \cdot \left(\begin{array}{rrrr}3&7&4&1\\5&6&4&0 \end{array}\right) =\left(\begin{array}{rrrr} 13 & 19 & 12 & 1 \\ 9 & 21 & 12 & 3 \\ 20 & 24 & 16 & 0 \\ \end{array} \right)\)
(b) \(\displaystyle \left(\begin{array}{rrr} 1&2&3 \end{array}\right) \cdot \left(\begin{array}{r}4\\5\\6 \end{array}\right)=32\)
(c) \(\displaystyle \left(\begin{array}{r}4\\5\\6 \end{array}\right)\cdot \left(\begin{array}{rrr} 1&2&3 \end{array}\right)= \left(\begin{array}{rrr} 4 & 8 & 12 \\ 5 & 10 & 15 \\ 6 & 12 & 18 \end{array}\right)\)
(d) \(\displaystyle \left(\begin{array}{rrrr} 3&7&4&1\\5&6&4&0 \end{array}\right) \cdot \left(\begin{array}{rrrr}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1 \end{array}\right)= \left(\begin{array}{rrrr} 3 & 7 & 4 & 1 \\ 5 & 6 & 4 & 0 \\ \end{array}\right)\)
(e) \(\displaystyle \left(\begin{array}{rr} 1&0\\0&1 \end{array}\right) \cdot \left(\begin{array}{rrrr}3&7&4&1\\5&6&4&0 \end{array}\right)= \left(\begin{array}{rrrr} 3 & 7 & 4 & 1 \\ 5 & 6 & 4 & 0 \\ \end{array}\right)\\\)
We conclude this section with another important property of the matrix product:
Theorem 7.15 Let \(\mathbf A\) and \(\mathbf B\) be two matrices of such order that the product \(\mathbf A\mathbf B\) can be formed. Then the following holds: \[ \begin{gathered} {(\mathbf A\mathbf B)}^\top={\mathbf B}^\top {\mathbf A}^\top. \end{gathered} \]
We leave it to interested readers to verify this relationship using an example.
7.2.3 Special Products
An important special case of matrix multiplication is the multiplication of a matrix by a column vector. It should be completely clear that you can always multiply a (corresponding) column vector to the right of a matrix. The result is again a column vector. \[ \begin{gathered} \begin{array}{ccccc} \mathbf A & \cdot & \mathbf b & = & \mathbf c \\ m\times n & \leftrightarrow &n\times 1 & & m \times 1 \end{array} \end{gathered} \]
Exercise 7.16 Calculate the product of \[ \begin{gathered} \mathbf A=\left(\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{array}\right)\quad\text{and}\quad \mathbf b= \left(\begin{array}{c} 1\\2\\3\end{array}\right). \end{gathered} \]
Solution: Using the Falk schema: \[ \begin{gathered} \left(\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{array}\right)\left(\begin{array}{c} 1\\2\\3\end{array}\right)= \left(\begin{array}{r} 14\\32\\50\end{array}\right). \end{gathered} \] □
We have already encountered the product matrix × column vector in Chapter 6. Let’s recall the general form of a linear system of equations: \[ \begin{gathered} \begin{array}{rcrcrcr} a_{11}x_1 &+& a_{12}x_2 &+\cdots+& a_{1n}x_n &=& b_1 \\ a_{21}x_1 &+& a_{22}x_2 &+\cdots+& a_{2n}x_n &=& b_2 \\ \vdots && \vdots && \vdots && \vdots\\ a_{m1}x_1 &+& a_{m2}x_2 &+\cdots+& a_{mn}x_n &=& b_m \\ \end{array} \end{gathered} \] Upon closer inspection, you realize that the left-hand sides of the equations are actually sums of products. But that’s exactly how we form the matrix product! This means: Every linear system of equations can be written using matrix multiplication as a matrix equation \[ \begin{gathered} \mathbf A\cdot \mathbf x=\mathbf b \end{gathered} \tag{7.7}\] Here, \(\mathbf A\) denotes the coefficient matrix, \(\mathbf x\) the vector of unknown variables, and \(\mathbf b\) the vector on the right-hand side of the system of equations.
Another important special case of matrix multiplication is the multiplication of a row vector with a matrix. Again, make it clear to yourself that only a row vector can be multiplied from the left to a matrix with more than one row. The result is again a row vector: \[ \begin{gathered} \begin{array}{ccccc} {\mathbf a}^\top & \cdot & \mathbf B &=& {\mathbf c}^\top \\ 1\times m & \leftrightarrow &m \times n && 1 \times n \end{array} \end{gathered} \tag{7.8}\]
Exercise 7.18 Calculate the product: \[ \begin{gathered} {\mathbf a}^\top :=\left(\begin{array}{ccc} 1 & 2 & 3\end{array}\right)\quad\text{and}\quad \mathbf B:= \left(\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{array}\right). \end{gathered} \]
Solution: Using the Falk scheme we find: \[ \begin{gathered} \left(\begin{array}{ccc} 1 & 2 & 3\end{array}\right) \cdot \left(\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{array}\right) = \left(\begin{array}{ccc} 30 & 36 & 42\end{array}\right). \end{gathered} \]
We would like to briefly mention one last special case. If in (7.8) the matrix \(\mathbf B\) has only one column, then we form the product of a row vector with a column vector: \[ \begin{gathered} \begin{array}{ccccc} {\mathbf a}^\top & \cdot & \mathbf b &=& \mathbf c \\ 1 \times m & & m \times 1 && 1 \times 1 \end{array} \end{gathered} \tag{7.9}\] The result is a matrix of order \(1 \times 1\), which is an ordinary number.
Exercise 7.19 Calculate the product \(\displaystyle \left(\begin{array}{ccc}1 & 2 & 3\end{array}\right) \left(\begin{array}{r}4\\-1\\2\end{array}\right).\)
Solution: \[ \begin{gathered} \left(\begin{array}{ccc}1 & 2 & 3\end{array}\right) \left(\begin{array}{r}4\\-1\\2\end{array}\right) = 1 \cdot 4 + 2 \cdot (-1) + 3 \cdot 2 = 8. \end{gathered} \] □
This specific product is probably known to you by the name scalar product of vectors.
An important special case of the multiplication of a row vector with a column vector occurs when the two factors are equal: \[ \begin{gathered} {\mathbf a}^\top \mathbf a = a_1^2 + a_2^2 + \ldots + a_n^2. \end{gathered} \tag{7.10}\] Therefore, this product yields the sum of the squares of the components of a vector!
7.3 Matrices in Planning Calculations
7.3.1 Basic Equation of Requirements Planning
One of the most important economic applications of matrix calculus is requirements planning. In this context, matrices represent requirements matrices, which are structures of quantities in tabular form that represent the used production technology. This technology is linear, meaning that an increase in inputs by a factor \(\alpha\) results in an increase of output by the same factor.
We will connect this to the introductory example in the section 6.3.2, where we explained the concept of requirements vectors. Calculations involving requirements vectors can be very simply and clearly represented in matrix notation.
Let’s look at Exercise 6.24 again.
A furniture store offers among other items two types of DIY bookshelves. Type A has a height of 200 cm, Type B is the smaller variant with a height of 110 cm. For Type A, each unit requires 5 \(m^2\) of veneered planks, while Type B needs 3 \(m^2\) of planks. The manufacturing (cutting the planks, drilling and packaging) is fully automated. Type A takes 8 minutes of machine time for manufacturing, Type B 6 minutes.
We calculated the input vector for the output of 50 shelves A and 20 shelves B by a linear combination \[ \begin{gathered} 50\mathbf a+20\mathbf b= 50\left(\begin{array}{c}5\\8 \end{array}\right)+ 20\left(\begin{array}{c}3\\6 \end{array}\right)= \left(\begin{array}{c}310\\520 \end{array}\right). \end{gathered} \] This calculation step can also be represented in matrix notation. For this, we combine the to-be-produced quantities into an output vector \(\mathbf x\): \[ \begin{gathered} \mathbf x=\left(\begin{array}{c} 50\\20 \end{array}\right). \end{gathered} \] Furthermore, we form a requirements matrix out of the requirements vectors so that each requirements vector becomes a column of this matrix: \[ \begin{gathered} \mathbf A=\left( \begin{array}{cc} 5 & 3\\ 8 & 6 \end{array}\right). \end{gathered} \] The required input vector (input quantities) \(\mathbf b\) now results from a simple product of the requirements matrix with the output vector: \[ \begin{gathered} \mathbf b = \mathbf A \mathbf x = \left( \begin{array}{cc} 5 & 3\\ 8 & 6 \end{array}\right)\left(\begin{array}{c} 50\\20 \end{array}\right) = \left(\begin{array}{c} 310\\520 \end{array}\right). \end{gathered} \]
A company manufactures three final products \(B_1,B_2\) and \(B_3\) from four initial products \(A_1, A_2, A_3\) and \(A_4\). To produce 1 \(B_1\), 3 \(A_1\), 2 \(A_2\) and 4 \(A_4\) are required. In the production of 1 \(B_2\), 2 \(A_1\), 4 \(A_2\), 2 \(A_3\) and 1 \(A_4\) are processed. To make 1 \(B_3\), 1 \(A_2\) and 2 \(A_3\) are needed. This quantity structure has the form of a requirements table: \[ \begin{gathered} \begin{array}{c|ccc} & B_1 & B_2 & B_3\\ \hline A_1 & 3 & 2 & 0\\ A_2 & 2 & 4 & 1\\ A_3 & 0 & 2 & 2\\ A_4 & 4 & 1 & 0 \end{array}\quad\longrightarrow: \mathbf A= \left(\begin{array}{ccc} 3 & 2 & 0\\ 2 & 4 & 1\\ 0 & 2 & 2\\ 4 & 1 & 0 \end{array}\right) \end{gathered} \] The matrix \(\mathbf A\), created from the requirements table, is called the requirements matrix. It quantitatively describes the transformation of the inputs \(A_1, A_2, A_3\) and \(A_4\) into the outputs \(B_1,B_2\) and \(B_3\). The individual columns are the requirements vectors of the final products.
The fundamental task of requirements planning, the parts requirement calculation, is now: if a specific production order is present, which input quantities are required to fulfill this order?
For example, let’s assume 10 units of \(B_1\), 15 units of \(B_2\) and 20 units of \(B_3\) are to be delivered. We summarize these quantities in an output vector \(\mathbf x\): \[ \begin{gathered} \mathbf x=\left(\begin{array}{r}10\\15\\20\end{array}\right). \end{gathered} \] We can now immediately state how much of \(A_1\) will be needed to fulfill this order. The information for this can be found in the 1st row of the requirements matrix \(\mathbf A\) and in the output vector \(\mathbf x\): \[ \begin{gathered} \text{Demand for $A_1$: }\quad 3\cdot 10+2\cdot 15+0\cdot 20=60 \end{gathered} \] This is obviously the product of the 1st row of \(\mathbf A\) with the vector \(\mathbf x\). In a similar manner, the demand for \(A_2,A_3\) and \(A_4\) is calculated as the product of the 2nd, 3rd and 4th row of \(\mathbf A\) with \(\mathbf x\). In short, the input quantities are the components of the vector \(\mathbf b\), which results as the product of the requirements matrix with the output vector: \[ \begin{gathered} \mathbf b=\mathbf A\mathbf x= \left(\begin{array}{ccc} 3 & 2 & 0\\ 2 & 4 & 1\\ 0 & 2 & 2\\ 4 & 1 & 0 \end{array}\right)\left(\begin{array}{r}10\\15\\20\end{array} \right)=\left(\begin{array}{r}60\\100\\70\\55\end{array}\right). \end{gathered} \]
The relationship between requirements matrix, output vector, and input vectors identified in the last two examples is so significant that we record:
Definition 7.22 (Fundamental Equation of Requirements Planning) Let \(\mathbf x\) be the output vector and \(\mathbf A\) the requirements matrix. Then the required inputs \(\mathbf b\) are: \[ \begin{gathered} \mathbf b=\mathbf A\cdot \mathbf x. \end{gathered} \tag{7.11}\]
Exercise 7.23 A company also manufactures electronic modules \(B_1, B_2\) and \(B_3\). This requires capacitors (C) and resistors (R). The demand for capacitors and resistors and the available inventory levels can be seen in the following table:
\[ \begin{array}{|l|rrr|r|} \hline & B_1 & B_2 & B_3 & \text{Inventory}\\ \hline C & 5 & 2 & 9 & 2000\\ R & 2 & 1 & 6 & 1200\\ \hline \end{array} \]
An order specifies the delivery of 100 pcs of \(B_1\), 150 pcs of \(B_2\) and 120 pcs of \(B_3\).
Can the order be fulfilled with the existing inventory levels?
If so, what is the inventory level after executing the order?
Solution: We calculate the required input using the basic equation (7.11) of requirements planning. Let \(\mathbf A\) denote the requirements matrix, \(\mathbf x\) the output vector, and \(\mathbf b\) the input vector. The basic equation is \(\mathbf A\mathbf x=\mathbf b\), and in numbers \[ \begin{gathered} \mathbf b=\left( \begin{array}{rrr} 5 & 2 & 9\\ 2 & 1 & 6 \end{array}\right) \left(\begin{array}{r} 100\\ 150\\ 120 \end{array}\right) = \left(\begin{array}{r} 1880\\ 1070 \end{array}\right). \end{gathered} \] This is the required input vector for the planned output. We now compare the available inventory with the required input: \[ \begin{gathered} \text{Beginning inventory } \mathbf a= \left(\begin{array}{r} 2000\\ 1200 \end{array}\right) ,\quad\text{Ending inventory } \mathbf e =\mathbf a-\mathbf b = \left(\begin{array}{r} 120\\ 130 \end{array}\right). \end{gathered} \] The order can be executed, since \(\mathbf e\ge \mathbf{0}\), that is, there are no shortages.
7.3.2 Cost Side of Requirements Planning
A manufacturer produces products \(B_1, B_2, \ldots, B_n\) and requires raw materials \(A_1, A_2, \ldots, A_r\). The requirements matrix is \[ \begin{gathered} \begin{array}{c|cccc} &B_1&B_2&\ldots &B_n\\ \hline A_1&a_{11}&a_{12}& \ldots&a_{1n}\\ A_2&a_{21}&a_{22}& \ldots&a_{2n}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ A_r&a_{r1}&a_{r2}&\ldots&a_{rn}\\ \end{array} \quad\longrightarrow :\quad \mathbf A=\left(\begin{array}{cccc} a_{11}&a_{12}& \ldots&a_{1n}\\ a_{21}&a_{22}& \ldots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{r1}&a_{r2}&\ldots&a_{rn} \end{array}\right) \end{gathered} \] Let \({\mathbf p}^\top =(p_1,p_2,\ldots,p_r)\) be the vector of raw material prices and the vector \(\mathbf x\) contain the planned output quantities, i.e. \({\mathbf x}^\top =(x_1, x_2,\ldots,x_n)\).
We now ask the following questions:
How high are the total costs of the order represented by \(\mathbf x\)?
What are the production costs of the individual products?
Of course, it is possible to answer these questions very simply without the use of matrix calculations. However, our aim is to see how matrix calculations can provide a clear representation of the answer.
The total costs can be represented by a simple matrix product. As we know, we obtain the quantity vector \(\mathbf b\) of raw materials needed for production \(\mathbf x\) by \[ \begin{gathered} \mathbf b=\mathbf A\cdot \mathbf x. \end{gathered} \] On the other hand, the costs \(K\) for the processed raw material quantities \(\mathbf b\) are given by the product \[ \begin{gathered} K=p_1b_1+p_2b_2+\cdots+ p_rb_r= {\mathbf p}^\top \cdot \mathbf b. \end{gathered} \] From this, by substituting the equations into one another and from the associative law: \[ \begin{gathered} K={\mathbf p}^\top \cdot \mathbf b={\mathbf p}^\top \cdot (\mathbf A\cdot \mathbf x)=({\mathbf p}^\top \cdot \mathbf A)\cdot \mathbf x. \end{gathered} \tag{7.12}\] This is the matrix equation that represents the total costs.
The row vector \({\mathbf c}^\top ={\mathbf p}^\top \cdot \mathbf A\) has a simple and important interpretation. It contains the costs of individual products: \[ \begin{gathered} {\mathbf p}^\top \cdot \mathbf A= (p_1,p_2,\ldots,p_r) \left( \begin{array}{ccc} a_{11} & \ldots & a_{1n} \\ a_{21} & \ldots & a_{2n} \\ \vdots & \ddots & \vdots \\ a_{r1} & \ldots & a_{rn} \end{array}\right)=(c_1,c_2,\ldots,c_n) ={\mathbf c}^\top . \end{gathered} \]
Exercise 7.24 A manufacturer produces two products \(B_1\) and \(B_2\). He requires raw materials \(A_1, A_2\), and \(A_3\). The production takes place at two different locations \(S_1\) and \(S_2\). Although the same production technology is used at both locations, the purchase prices of raw materials differ between these locations. The requirement for raw materials as well as their purchase prices in \(S_1\) and \(S_2\) are given by:
\[ \begin{array}{|c|rr|rr|} \hline & B_1 & B_2 & p_1 & p_2\\ \hline A_1 & 3 & 4 & 10 & 9\\ A_2 & 2 & 1 & 2 & 3\\ A_3 & 4 & 6 & 3 & 4\\ \hline \end{array} \]
How high are the production costs of \(B_1\) and \(B_2\) at both locations?
500 units of \(B_1\) and 200 units of \(B_2\) are to be produced. What are the total costs incurred at locations \(S_1\) and \(S_2\)?
Solution: From the information given, we find: \[ \begin{gathered} \text{Requirement matrix: }\mathbf A=\left(\begin{array}{cc} 3 & 4\\ 2 & 1\\ 4 & 6 \end{array} \right), \mathbf p_1=\left(\begin{array}{r}10\\2\\3 \end{array}\right),\mathbf p_2=\left(\begin{array}{r}9\\3\\4 \end{array}\right). \end{gathered} \]
(a) The production costs at the two locations are: \[ \begin{gathered} \text{Costs at $S_1$:}\quad {\mathbf c_1}^\top = {\mathbf p_1}^\top \cdot \mathbf A= (10,2,3) \left(\begin{array}{cc} 3 & 4\\ 2 & 1\\ 4 & 6 \end{array} \right)=(46,60).\\ \text{Costs at $S_2$:}\quad {\mathbf c_2}^\top = {\mathbf p_2}^\top \cdot \mathbf A= (9,3,4) \left(\begin{array}{cc} 3 & 4\\ 2 & 1\\ 4 & 6 \end{array} \right)=(49,63). \end{gathered} \] (b) To calculate the total costs, we need to multiply by the output vector from the right \[ \begin{gathered} \mathbf x=\left(\begin{array}{c}500\\200\end{array}\right) \end{gathered} \] This results in: \[ \begin{gathered} K_1=({\mathbf p_1}^\top \cdot \mathbf A)\cdot \mathbf x=(46,60) \left(\begin{array}{c}500\\200\end{array}\right)=35000,\\ K_2=({\mathbf p_2}^\top \cdot \mathbf A)\cdot \mathbf x=(49,63) \left(\begin{array}{c}500\\200\end{array}\right)=37100. \end{gathered} \] □
Exercise 7.25 In a company, the products \(P_1, P_2\) and \(P_3\) are made using two machines \(M_1\) and \(M_2\). The required machine times per piece (in minutes) as well as the machine costs can be taken from the following table:
\[ \begin{array}{|c|rrr|r|} \hline & P_1 & P_2 & P_3 & \text{Costs/Hour}\\ \hline M_1 & 20 & 4 & 10 & 150\qquad\enspace\\ M_2 & 5 & 8 & 12 & 120\qquad\enspace\\ \hline \end{array} \]
An order requires the delivery of 200 pieces \(P_1\), 100 pieces \(P_2\) and 180 pieces \(P_3\). Calculate the total cost of this order.
Solution: Let’s denote \(\mathbf A\) as the requirement matrix, \(\mathbf x\) as the output vector and \(\mathbf k\) as the cost vector for the machine times: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rrr} 20 & 4 & 10\\5 & 8 & 12 \end{array}\right),\quad \mathbf x=\left(\begin{array}{r}200\\100\\180\end{array}\right),\quad \mathbf k=\frac{1}{60}\left(\begin{array}{r}150\\120\end{array}\right). \end{gathered} \] Note that we’re calculating costs per minute here. The total costs of the order then are \[ \begin{aligned} c&={\mathbf k}^\top \cdot \mathbf A\cdot \mathbf x\\ &=\frac{1}{60}\left(\begin{array}{rr}150 & 120\end{array}\right) \left(\begin{array}{rrr} 20 & 4 & 10\\5 & 8 & 12 \end{array}\right)\left(\begin{array}{r}200\\100\\180\end{array}\right)\\ &=\frac{1405200}{60}=23420\text{ CU}. \end{aligned} \] □
Exercise 7.26 In a company, assemblies \(B_1\) and \(B_2\) are manufactured from components \(A_1\) and \(A_2\), which are then assembled in a further processing step into devices \(E_1, E_2\) and \(E_3\). A delivery order requires the production of 100 pieces of \(E_1\), 200 pieces of \(E_2\) and 50 pieces of \(E_3\). The following is known about the quantity requirements at the two production stages:
\[ \begin{gathered} \begin{array}{|c|cc|r|} \hline &B_1 & B_2 & \text{Stock}\\ \hline A_1 & 4 & 6 &14000 \\ A_2 & 7 & 0 &350\\ \hline \end{array}\hspace{1cm} \begin{array}{|c|rrr|} \hline &E_1 & E_2 & E_3\\ \hline B_1 & 5 & 2 &1 \\ B_2 & 0 & 10 &20\\ \hline \end{array} \end{gathered} \]
A brief calculation convinces the production manager that this order cannot be executed with the available stock. The only short-term option is to purchase finished assemblies from a competing company. However, this company charges unit prices of 12 and 15 CU respectively for \(B_1\) and \(B_2\), while the production of \(B_1\) and \(B_2\) only costs 10 and 12 CU per unit respectively. What are the additional costs if the stock is completely used up? □
Solution: The requirement matrix and the desired output vector are: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rrr} 5 & 2 & 1\\ 0 & 10 & 20 \end{array}\right), \quad \mathbf x=\left(\begin{array}{r}100\\200\\50 \end{array}\right). \end{gathered} \] For the output \(\mathbf x\), we need the following numbers of subassemblies \(B_1\) and \(B_2\): \[ \begin{gathered} \mathbf q=\mathbf A\mathbf x=\left(\begin{array}{rrr} 5 & 2 & 1\\ 0 & 10 & 20 \end{array}\right) \left(\begin{array}{r} 100\\200\\50 \end{array}\right) = \left(\begin{array}{r} 950\\3000 \end{array} \right). \end{gathered} \] On the other hand, we must ask which quantities \(b_1\) and \(b_2\) of the subassemblies \(B_1\) and \(B_2\) can be produced from the existing stock levels. This question leads to the solution of a system of equations: \[ \begin{gathered} \left( \begin{array}{cc} 4 & 6 \\ 7 & 0 \end{array} \right) \cdot \left( \begin{array}{r} b_1\\ b_2 \end{array} \right)= \left( \begin{array}{r} 14\,000 \\ 350 \end{array} \right) \quad \implies \quad \begin{array}{rcrcr} 4b_1 &+& 6b_2 &=& 14000\\ 7b_1 & & &=& 350 \end{array} \end{gathered} \] This system of equations has the solution \(b_1=50\), \(b_2=2300\). Thus, the producible output vector of subassemblies is \[ \begin{gathered} \mathbf b=\left(\begin{array}{r}50\\2300\end{array} \right). \end{gathered} \] From the difference, we obtain the required quantities to be purchased: \[ \begin{gathered} \mathbf q-\mathbf b=\left(\begin{array}{r}900\\700\end{array}\right). \end{gathered} \] We calculate the additional costs incurred by multiplying the price difference vector \[ \begin{gathered} \Delta\mathbf p=\left(\begin{array}{r}2\\3\end{array}\right) \end{gathered} \] by the vector of purchase quantities: \[ \begin{gathered} c=\Delta {\mathbf p}^\top \cdot (\mathbf q-\mathbf b) = 2\cdot 900+3\cdot 700 =3900. \end{gathered} \] □
7.3.3 Multi-stage Production Processes
In practice, production processes are not as simply structured as in the previous examples; rather, they include several process stages, in which intermediate products are manufactured from inputs that come from technologically upstream stages. The outputs of one stage are further processed in one or more downstream process stages until finally, the finished end products emerge at the end of the chain. For each production stage, the quantitative relationship between the inputs and the outputs is known and is given by a requirement matrix.
What quantities of initial products must be available to produce a given output of final products?
Let’s consider as an example a three-stage process in which the stages are strictly arranged in a sequence. Such an arrangement is also called a Flow Shop. From the \(m\) initial products \(A_1,\ldots,A_m\), \(n\) intermediate products \(P_1,\ldots,P_n\) are manufactured in the first stage. The corresponding requirement matrix is \(\mathbf A_{12}\). From \(P_1,\ldots,P_n\) in the second stage, \(r\) intermediate products \(Q_1,\ldots,Q_r\) are produced, and we call the requirement matrix for this stage \(\mathbf A_{23}\). Finally, from \(Q_1,\ldots,Q_r\), the \(s\) final products \(E_1,\ldots,E_s\) are manufactured. The requirement matrix for the third stage is \(\mathbf A_{34}\).
Schematically, this process can be represented as follows:
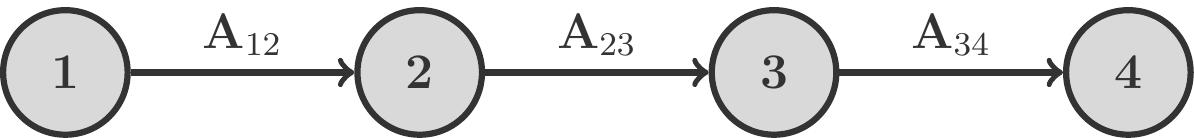
\[ \begin{gathered} \begin{array}{|cccc|} \hline\rowcolor{mgray}\rule{0pt}{11pt} \text{Stage} & \text{Inputs} & \text{Outputs} & \text{Requirement Matrix}\\ \hline \rule{0pt}{13pt} 1\to 2 & A_1,\ldots, A_m & P_1,\ldots, P_n & \mathbf A_{12}\\ 2\to 3 & P_1,\ldots, P_n & Q_1,\ldots, Q_r & \mathbf A_{23}\\ 3\to 4 & Q_1,\ldots, Q_r & E_1,\ldots, E_s& \mathbf A_{34}\\[2pt] \hline \end{array} \end{gathered} \] Now let’s say we are given an order vector \(\mathbf x\), and we are looking for the necessary inputs of the 1st stage. These quantities are summarized in a vector \(\mathbf a\).
To find \(\mathbf a\), we work our way through the manufacturing process from right to left. So we first look at the last stage of the production process. The inputs for \(Q_1,\ldots,Q_r\) of the last stage, which we combine into a vector \(\mathbf q\), result from the product: \[ \begin{gathered} \mathbf q=\mathbf A_{34}\cdot\mathbf x \end{gathered} \tag{7.13}\] Now \(\mathbf q\) is simultaneously the output vector of the 2nd stage. To produce this \(\mathbf q\), we need input quantities \(\mathbf p\) of products \(P_1,\ldots,P_n\), where \[ \begin{gathered} \mathbf p=\mathbf A_{23}\cdot\mathbf q \end{gathered} \tag{7.14}\] If \(\mathbf p\) is the output of the 1st stage, then the necessary amounts of \(A_1,\ldots,A_m\) are just those of the input vector \(\mathbf a\): \[ \begin{gathered} \mathbf a=\mathbf A_{12}\cdot\mathbf p \end{gathered} \tag{7.15}\] We now insert (7.13) into (7.14) and in turn that into (7.15). In doing so, we make use of the associative law of matrix multiplication: \[ \begin{aligned} \mathbf a=\mathbf A_{12}\mathbf p&=\mathbf A_{12}(\mathbf A_{23}\mathbf q)\\ &=\mathbf A_{12}\mathbf A_{23}(\mathbf A_{34}\mathbf x)\\ &=\mathbf A_{12}\mathbf A_{23}\mathbf A_{34}\mathbf x=\mathbf A\mathbf x \end{aligned} \] \(\mathbf A\) denotes the global requirement matrix for the quantitative relationship between initial and final products. We note: \(\mathbf A\) is the product of the requirement matrices along the only path through the process diagram, where this matrix product is formed exactly in the technological sequence.
Exercise 7.28 From 3 initial products \(A_1,A_2\), and \(A_3\), intermediate products \(P_1\) and \(P_2\) are manufactured in the first stage, from these in the second stage intermediate products \(Q_1\) and \(Q_2\), and from those finally in the third stage the final products \(E_1,E_2\), and \(E_3\). The structures of the production stages are given by the following requirement matrices: \[ \begin{gathered} \mathbf A_{12}=\left(\begin{array}{rr} 4 & 0\\ 2 & 2\\ 0 & 7 \end{array}\right), \mathbf A_{23}= \left(\begin{array}{rr} 10 & 20\\ 7 & 15 \end{array}\right), \mathbf A_{34}= \left(\begin{array}{rrr} 8 & 20 & 10\\ 5 & 10 & 15 \end{array}\right). \end{gathered} \]
1 piece of \(E_1\) and \(E_2\) is to be produced, as well as 2 pieces of \(E_3\). What inventory levels of \(A_1, A_2\), and \(A_3\) must be available for this?
Solution: The global requirement matrix is \[ \begin{aligned} \mathbf A = \mathbf A_{12} \mathbf A_{23} \mathbf A_{34} &= \left(\begin{array}{rr} 4 & 0\\ 2 & 2\\ 0 & 7 \end{array}\right) \left(\begin{array}{rr} 10 & 20\\ 7 & 15 \end{array}\right) \left(\begin{array}{rrr} 8 & 20 & 10\\ 5 & 10 & 15 \end{array}\right) \\[5pt] &=\left(\begin{array}{rrr} 720 & 1600 & 1600\\ 622 & 1380 & 1390\\ 917 & 2030 & 2065 \end{array}\right). \end{aligned} \] In order to produce the output vector \({\mathbf x}^\top = (1,1,2)\), there is a need for initial products amounting to \[ \begin{gathered} \mathbf a = \mathbf A \mathbf x = \left(\begin{array}{rrr} 720 & 1600 & 1600\\ 622 & 1380 & 1390\\ 917 & 2030 & 2065 \end{array}\right) \left(\begin{array}{r}1\\1\\2\end{array}\right) = \left(\begin{array}{r} 5520\\ 4782\\ 7077 \end{array}\right). \end{gathered} \] □
Remark 7.29 (Smart Calculation) Multiplying matrices is an elaborate process. If \(\mathbf A\) is of order \(m \times n\) and \(\mathbf B\) is of order \(n \times k\), then we need for the product \(\mathbf A \cdot \mathbf B\) a total of: \[ \begin{gathered} \text{Multiplications: } m \cdot n \cdot k, \quad\text{Additions: }m \cdot (n-1) \cdot k \end{gathered} \] An obvious way to carry out the calculation in Exercise 7.28 would be this: \[ \begin{gathered} \mathbf a = (((\mathbf A_{12} \mathbf A_{23}) \mathbf A_{34}) \mathbf x) \end{gathered} \tag{7.16}\] Transferred to a Falk scheme, this would mean that we calculate in such a way that the Falk scheme is staggered to the right: \[ \begin{gathered} \begin{array}{rr|rr|rrr|r} \mathbf A_{12} & & {\mathbf A_{23}} & & {\mathbf A_{34}} & & & {\mathbf x}\\ \hline & & & & & & & 1\\ & & 10 & 20 & 8 & 20 & 10 & 1\\ & & 7 & 15 & 5 & 10 & 15 & 2\\ \hline 4 & 0 & 40 & 80 & 720 & 1600 & 1600 & 5520 \\ 2 & 2 & 34 & 70 & 622 & 1380 & 1390 & 4782 \\ 0 & 7 & 49 & 105 & 917 & 2030 & 2065 & 7077 \\ \end{array} \end{gathered} \] That means we first multiply \(\mathbf A_{12}\) with \(\mathbf A_{23}\). The result is then multiplied with \(\mathbf A_{34}\). Finally, we multiply the last result with the column vector \(\mathbf x\). That’s exactly what the bracketing (7.16) means. The computational effort amounts to: 39 multiplications and 21 additions.
The effort can be more than halved if we choose a different bracketing, which we are allowed to do, because an associative law applies. We can also place the brackets like this: \[ \begin{gathered} \mathbf a = (\mathbf A_{12}(\mathbf A_{23}(\mathbf A_{34} \mathbf x))) \end{gathered} \] This would mean that we stack the Falk scheme from top to bottom: \[ \begin{gathered} \begin{array}{rrr|rl} & & & 1&\\ & & & 1&=\mathbf x\\ & & & 2&\\ \hline 8 & 20 & 10 &48\\ 5 & 10 & 15 &45 & =\mathbf A_{34} \mathbf x\\ \hline & 10 & 20 &1380\\ & 7 & 15 &1011&=\mathbf A_{23}(\mathbf A_{34} \mathbf x)\\ \hline & 4 & 0 &5520\\ & 2 & 2 &4782&=\mathbf A_{12}(\mathbf A_{23}(\mathbf A_{34} \mathbf x)) \\ & 0 & 7 &7077 \end{array} \end{gathered} \] In fact, the effort has almost halved. Now only 16 multiplications and 9 additions are required.
Processes with Branches
The problem becomes even more interesting when the production process has branches.
From the \(m\) initial products \(A_1,\ldots,A_m\), \(n\) intermediate products \(P_1,\ldots,P_n\) are manufactured in the first stage. Let’s call the corresponding demand matrix \(\mathbf A_{12}\).
From \(P_1,\ldots,P_n\), \(r\) intermediate products \(Q_1,\ldots,Q_r\) are made in the second stage. We will refer to the demand matrix of this stage as \(\mathbf A_{23}\).
Finally, the \(s\) final products \(E_1,\ldots,E_s\) are produced from \(Q_1,\ldots,Q_r\). The demand matrix of the third stage is \(\mathbf A_{34}\).
A certain number of the intermediate products \(P_i\) are also needed in the final production without further processing. This demand is represented by another demand matrix \(\mathbf A_{24}\).
Again, what is sought is the global demand matrix of the production process.
The structure of this production process can be schematically represented as follows:
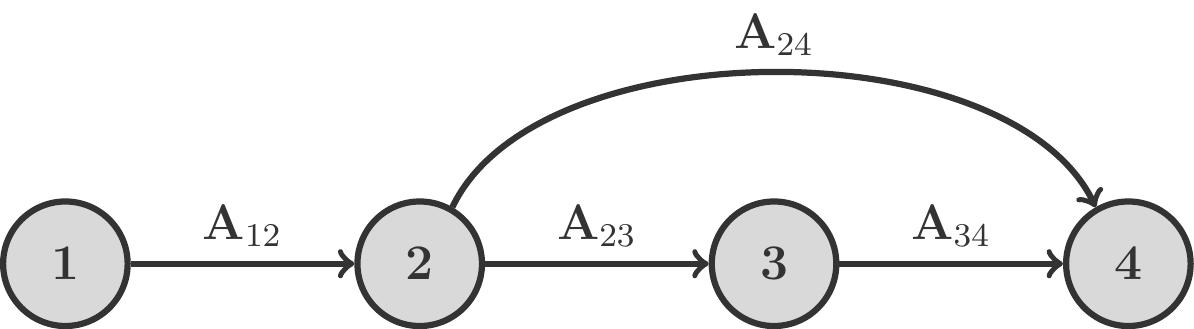
To solve this problem, we can proceed just as we did before: we start at the last stage and work our way from right to left back to the starting point of the process, calculating the need for intermediate products. However, we must take into account that two material flows come together in the last stage.
We determine all possible paths through the process diagram: In our example, we obtain: \[ \begin{gathered} \begin{array}{lcccccl} \text{1st path: } & 1 & 2 & 3 & 4 & \rightarrow & \mathbf A_{12}\mathbf A_{23}\mathbf A_{34}\\ \text{2nd path: } & 1 & 2 & 4 & & \rightarrow & \mathbf A_{12}\mathbf A_{24}\\ \hline \text{Sum: } & & & & & &\mathbf A_{12}\mathbf A_{23}\mathbf A_{34}+ \mathbf A_{12}\mathbf A_{24} \end{array} \end{gathered} \] Therefore, the demand matrix \(\mathbf A\), which directly connects the initial products with the final products, is \[ \begin{gathered} \mathbf A=\mathbf A_{12}\mathbf A_{23}\mathbf A_{34}+ \mathbf A_{12}\mathbf A_{24}=\mathbf A_{12}(\mathbf A_{23}\mathbf A_{34}+\mathbf A_{24}). \end{gathered} \] Note that we were able to bring out \(\mathbf A_{12}\) by applying the distributive law, thus even saving us a matrix multiplication.
An interesting special case occurs when a production factor \(A_k\) (e.g., energy) from the first stage is needed on every further stage.
Exercise 7.30 In a multi-stage chemical production process, intermediate products \(P_1\) and \(P_2\) are generated from two initial substances \(A_1\) and \(A_2\). These are processed into further products \(Q_1\) and \(Q_2\), from which the chemical substances \(E_1,E_2\) and \(E_3\) are finally produced in the last phase of the process. Each phase of the process requires process heat (in kWh) to maintain the chemical reactions. The quantity structures and heat requirements of the process steps are as follows:
\[ \begin{gathered} \begin{array}{c|cc} & P_1 & P_2\\ \hline W & 5 & 4\\ A_1 & 2 & 0\\ A_2 & 0 & 3 \\ \end{array},\quad \begin{array}{c|rr} & Q_1 &Q_2\\ \hline W & 10 & 8\\ P_1 & 2 & 0\\ P_2 & 1 & 4 \\ \end{array},\quad \begin{array}{c|rrr} & E_1 &E_2 &E_3\\ \hline W & 1 & 2 & 4\\ Q_1 & 1 & 2 & 0\\ Q_2 & 1 & 0 & 4 \\ \end{array} \end{gathered} \]
One unit each of the chemical substances \(E_1,E_2\) and \(E_3\) is to be produced. What amounts of the starting materials \(A_1\) and \(A_2\) are required for this, and what is the total demand for process heat?
Solution: We construct a multi-step process with branches of the following kind:
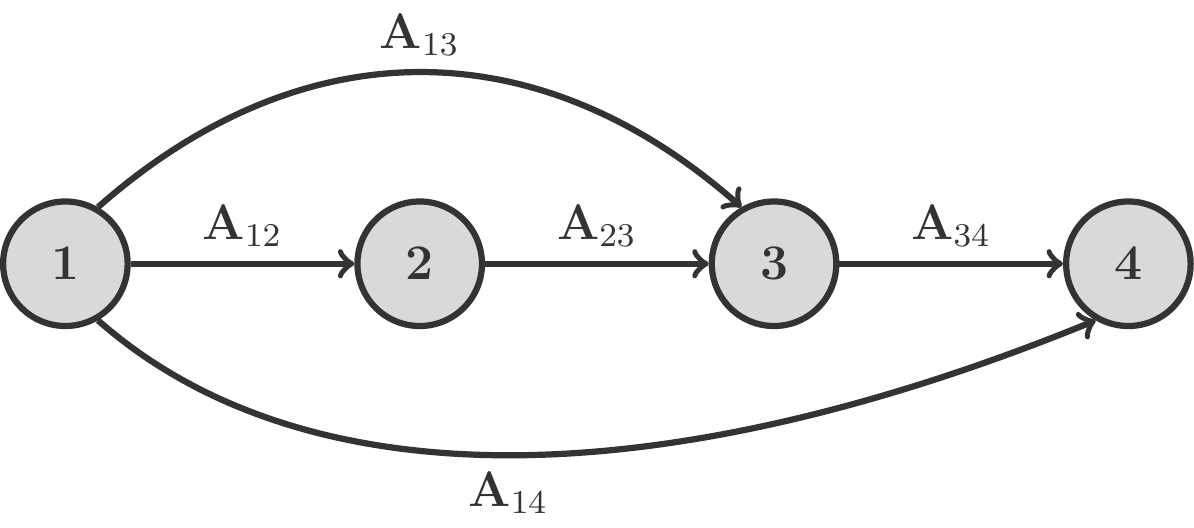
We are now dealing with five demand matrices, where the demand matrices \(\mathbf A_{13}\) and \(\mathbf A_{14}\) represent the heat demand during the production of \(Q_i\) and \(E_i\): \[ \begin{gathered} \mathbf A_{12}=\left(\begin{array}{cc} 5 & 4\\ 2 & 0\\ 0 & 3 \end{array}\right),\quad \mathbf A_{23}=\left(\begin{array}{cc}2 & 0\\1 & 4\end{array}\right), \quad \mathbf A_{34}=\left(\begin{array}{ccc}1 & 2 & 0\\1 & 0 & 4\end{array}\right)\\[5pt] \mathbf A_{13}=\left(\begin{array}{rr}10 & 8\\0 & 0\\0 & 0\end{array}\right),\quad \mathbf A_{14}=\left(\begin{array}{ccc}1 & 2 & 4\\0 & 0 & 0\\0 & 0 & 0\end{array} \right). \end{gathered} \] There are three paths through the process with associated demand matrices: \[ \begin{gathered} \begin{array}{ll} 1\to 2\to 3\to 4 & \mathbf A_{12}\mathbf A_{23}\mathbf A_{34}\\ 1\to 3\to 4 &\mathbf A_{13}\mathbf A_{34}\\ 1\to 4 &\mathbf A_{14}\\ \hline \text{global demand matrix} \mathbf A=& \mathbf A_{12}\mathbf A_{23}\mathbf A_{34} +\mathbf A_{13}\mathbf A_{34}+\mathbf A_{14} \end{array} \end{gathered} \] The output vector is \({\mathbf x}^\top =(1,1,1)\). If the calculation is carried out as explained in Remark 7.29, then we get: \[ \begin{aligned} \mathbf A\mathbf x&=\mathbf A_{12}\mathbf A_{23}\mathbf A_{34}\mathbf x + \mathbf A_{13}\mathbf A_{34}\mathbf x+\mathbf A_{14}\mathbf x\\[5pt] &=\left(\begin{array}{r} 122\\ 12\\ 69 \end{array}\right)+\left(\begin{array}{r} 70\\ 0\\ 0\end{array}\right)+ \left(\begin{array}{r}7\\0\\0\end{array}\right)= \left(\begin{array}{r} 199\\ 12\\ 69\end{array}\right). \end{aligned} \] Therefore, for this production plan, 199 kWh of process heat, 12 ME of \(A_1\) and 69 ME of \(A_2\) are required. □
7.4 The Inverse of a Matrix
7.4.1 The Concept of an Inverse Matrix
Inverse matrices are required to be able to solve linear matrix equations of the form \(\mathbf A\mathbf X=\mathbf C\) or similar.
Remark 7.31 Before we examine the problem for matrices, let’s recall how we solve such linear equations in the case of real numbers.
To solve the equation \(ax=c\) in the set of real numbers, one multiplies this equation with the number \(b:=\frac{1}{a}\), which has the property that \(b\cdot a=1\). This gives us \[ \begin{gathered} ax=c\;\Rightarrow\;b(ax)=bc \;\Rightarrow \; \underbrace{(ba)}_{=1}x=bc \;\Rightarrow\; x=bc=\frac{1}{a}\,c. \end{gathered} \] However, this only works if \(b\) exists, i.e., if \(a\neq 0\).
If one wishes to solve the matrix equation \(\mathbf A\mathbf X=\mathbf C\), one can proceed in a similar manner. One seeks a matrix \(\mathbf B\) with the property \(\mathbf B\mathbf A=\mathbf I\). We remember, the identity matrix \(\mathbf I\) is the neutral element of matrix multiplication, that is, \(\mathbf I\cdot\mathbf X=\mathbf X\). If we manage to find such a matrix \(\mathbf B\), then we can multiply the matrix equation from the left with this \(\mathbf B\) and obtain: \[ \begin{gathered} \mathbf B(\mathbf A\mathbf X)=\mathbf B\mathbf C \;\Rightarrow\; \underbrace{(\mathbf B\mathbf A)}_{=\mathbf I}\mathbf X=\mathbf B\mathbf C \; \Rightarrow\; \mathbf X=\mathbf B\mathbf C. \end{gathered} \tag{7.17}\] The question arises under which conditions a matrix \(\mathbf B\) with the property \(\mathbf B\mathbf A=\mathbf I\) exists and how one can find it. We only deal with this problem for square matrices. For rectangular matrices, the situation is more complicated.
Definition 7.32 Let \(\mathbf A\) be a square matrix of order \(n\times n\). \(\mathbf A\) is called regular, if there exists an \(n\times n\)-matrix \(\mathbf A^{-1}\) such that \[ \begin{gathered} \mathbf A\mathbf A^{-1}=\mathbf A^{-1}\mathbf A=\mathbf I. \end{gathered} \tag{7.18}\] In this case, \(\mathbf A^{-1}\) is called the inverse matrix of \(\mathbf A\).
If \(\mathbf A\) does not have an inverse, then \(\mathbf A\) is singular.
Aside from the identity matrix \(\mathbf I\), \(\mathbf A^{-1}\) is another example of a matrix that we apriori know commutes with \(\mathbf A\).
Let’s look at some examples.
Consider the matrices \[ \begin{gathered} \mathbf A=\left( \begin{array}{rr} 2 & 9 \\ 1 & 4 \end{array} \right), \qquad \mathbf A^{-1}=\left( \begin{array}{rr} -4 & 9 \\ 1 & -2 \end{array} \right). \end{gathered} \] By calculating the products, we find that indeed \(\mathbf A\mathbf A^{-1}=\mathbf I\) and \(\mathbf A^{-1}\mathbf A=\mathbf I\). In other words: \(\mathbf A\) is regular.
For the time being, we leave open how in this example the inverse \(\mathbf A^{-1}\) was calculated.
Not every square matrix is regular. The zero matrix \(\mathbf{0}\) obviously cannot have an inverse. Because if \(\mathbf{0}\) had an inverse, then there must be a matrix \(\mathbf{0}^{-1}\) with the property: \[ \begin{gathered} \mathbf{0}\cdot \mathbf{0}^{-1}=\mathbf I. \end{gathered} \] But that is impossible: whatever matrix we multiply with \(\mathbf{0}\), the result will always be the zero matrix. The zero matrix cannot have an inverse, it is therefore singular.
However, there are also matrices other than the zero matrix that are also singular. This is another difference between matrix calculations and calculations with real numbers.
The matrix \[ \begin{gathered} \mathbf A=\left( \begin{array}{rr} 1 & 2 \\ 2 & 4 \end{array} \right) \end{gathered} \] does not have an inverse.
To prove this claim, let’s set \[ \begin{gathered} \mathbf A^{-1}=\left(\begin{array}{cc}a & b\\c & d\end{array}\right), \end{gathered} \] where \(a, b, c\), and \(d\) are four unknown real numbers. How can we determine these?
For this we use the defining relation (7.18): \[ \begin{gathered} \mathbf A\mathbf A^{-1}=\mathbf I\Leftrightarrow \left( \begin{array}{rr} 1 & 2 \\ 2 & 4 \end{array} \right) \left(\begin{array}{cc}a & b\\c & d\end{array}\right)= \left(\begin{array}{cc}1 & 0\\0 & 1\end{array}\right), \end{gathered} \] or after expanding: \[ \begin{gathered} \left(\begin{array}{rr} a+2c & b+2d\\ 2a+4c & 2b+4d \end{array}\right)=\left(\begin{array}{cc}1 & 0\\0 & 1\end{array}\right). \end{gathered} \] Now we set equal component-wise: \[ \begin{gathered} \begin{array}{rcrcr} a & + & 2c &=& 1\\ 2a & + & 4c &=& 0 \end{array}\qquad \begin{array}{rcrcr} b&+& 2d &=&0\\ 2b &+& 4d &=& 1 \end{array} \end{gathered} \tag{7.19}\] These are two linear systems of equations with two equations and two unknowns each. If we write down the matrix of these systems, we notice something else: \[ \begin{gathered} \left(\begin{array}{cc|c} 1 & 2 & 1\\ 2 & 4 & 0 \end{array} \right)\qquad \left(\begin{array}{cc|c} 1 & 2 & 0\\ 2 & 4 & 1 \end{array} \right) \end{gathered} \tag{7.20}\] The left sides, i.e., the coefficient matrices of both systems, are completely identical, namely equal to the matrix \(\mathbf A\), whose inverse we are looking for.
Now, let’s take the first of these matrix equations and try to bring it into echelon form. This requires only a single elimination step: \[ \begin{gathered} Z_2\to Z_2-2Z_1:\quad \left(\begin{array}{cc|r} 1 & 2 & 1\\ \rowcolor{lgray}0 & 0 & -2 \end{array} \right) \end{gathered} \] The second row, however, corresponds to an unsolvable equation, the first system is unsolvable.
The same is true for the second system of equations in (7.20): \[ \begin{gathered} Z_2\to Z_2-2Z_1:\quad \left(\begin{array}{cc|r} 1 & 2 & 0\\ \rowcolor{lgray}0 & 0 & 1 \end{array} \right) \end{gathered} \] Neither of the two systems is solvable, thus, this matrix \(\mathbf A\) cannot have an inverse, it is singular.
So, there are infinitely many matrices in addition to the zero matrix that do not possess an inverse. That’s the bad news. But there is also good news:
Theorem 7.35 (Uniqueness) If a square matrix has an inverse, then it is uniquely determined.
7.4.2 Calculation of the Inverse
Elimination Algorithm
Our considerations regarding Example 7.34 incidentally provide us with an algorithm for calculating the inverse of a square matrix.
We saw that in both sets of equations (7.20), the left-hand sides are completely identical. This means that both systems have the same coefficient matrix, which is the matrix \(\mathbf A\). On the other hand, the right sides of the systems are the two columns of the identity matrix \(\mathbf I\).
The idea underlying our algorithm is quite straightforward:
Set up the calculation scheme \((\mathbf A\;|\;\mathbf I)\), which is an augmented matrix.
Perform legitimate simplification steps with the goal of creating a staircase step in each column of the left half.
If this is not possible, then \(\mathbf A\) is singular.
Otherwise, we have achieved: \[ \begin{gathered} (\mathbf A\;|\;\mathbf I) \to (\mathbf I\;|\;\mathbf A^{-1}) \end{gathered} \] That is, the inverse can be found in the right half of the scheme now.
Let’s take as an example the matrix \(\mathbf A\) from Example 7.33: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr}2 & 9\\1 & 4\end{array}\right). \end{gathered} \] The corresponding calculation scheme and elimination steps are: \[ \begin{aligned} (\mathbf A\;|\;\mathbf I)=&\left(\begin{array}{rr|rr}2 & 9 & 1 & 0\\1 & 4 & 0 & 1\end{array}\right)\\ Z_1\leftrightarrow Z_2: & \left(\begin{array}{rr|rr}1 & 4& 0& 1\\2 & 9 & 1 & 0\end{array}\right)\\ Z_2\to Z_2-2Z_1: &\left(\begin{array}{rr|rr}1 & 4 & 0 & 1\\ 0 & 1 & 1 & -2\end{array}\right)\\ Z_1\to Z_1-4Z_2: &\left(\begin{array}{rr|rr}1 & 0 & -4 & 9\\ 0 & 1 & 1 & -2\end{array}\right)=(\mathbf I\;|\;\mathbf A^{-1}) \end{aligned} \] Thus, we have found: \(\mathbf A^{-1}=\left(\begin{array}{rr}-4 & 9\\1 & -2\end{array}\right)\).
This adaptation of the elimination process is suitable for arbitrarily large matrices \(\mathbf A\), though the computational effort roughly increases proportional to \(n^3\), where \(n\) is the number of rows (columns) of \(\mathbf A\). Therefore, calculating inverse matrices is typically left to computer programs. For example, ordinary spreadsheet programs can be used for matrix calculations, including inverting matrices (provided they are regular).
We will therefore limit ourselves here to a useful formula for quickly inverting \(2\times 2\) matrices.
If one applies the elimination algorithm to a general \(2\times 2\) matrix, it yields a very simple formula for its inverse:
Theorem 7.36 (Inverse of a \(2\times 2\) Matrix) Let \(\mathbf A=\left(\begin{array}{cc}a & b\\c & d\end{array}\right)\). Then \[ \begin{gathered} \mathbf A^{-1}=\frac{1}{ad-bc}\left(\begin{array}{rr}d & -b\\-c & a\end{array} \right). \end{gathered} \tag{7.21}\] The number in the denominator of the fraction is called the determinant of the matrix \(\mathbf A\): \[ \begin{gathered} \det \mathbf A=\det\left(\begin{array}{cc}a & b\\c & d\end{array}\right)=ad-bc. \end{gathered} \] In the \(2\times 2\) case, this is formed according to the rule: product of the main diagonal minus product of the secondary diagonal.
Remark 7.37 a) The determinant is a number which can be greater, smaller, or equal to zero. If \(\det \mathbf A = 0\), then \(\mathbf A\) is singular, as follows immediately from (7.21).
b) The matrix on the right side of (7.21) is called the adjugate of \(\mathbf A\). It arises from \(\mathbf A\) in the following easily remembered way:
Swap the main diagonal,
Change the sign of the secondary diagonal.
Exercise 7.38 Form the inverse matrix of \[ \begin{gathered} \mathbf A = \left(\begin{array}{rr} 1 & 9 \\ 3 & 28 \end{array} \right). \end{gathered} \]
Solution: First, we calculate the determinant: \[ \begin{gathered} \det \mathbf A = 28\cdot1 - 9\cdot3 = 1 \end{gathered} \] Then, we construct the adjugate following the rule: swap the main diagonal, change the sign of the secondary diagonal: \[ \begin{gathered} \mathbf A^{-1} = \dfrac{1}{\det \mathbf A} \cdot \left(\begin{array}{rr} 28 & -9 \\ -3 & 1 \\ \end{array}\right) =\left(\begin{array}{rr} 28 & -9 \\ -3 & 1 \\ \end{array}\right) \end{gathered} \]
Exercise 7.39 Calculate the inverses of the matrices: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr}1 & 2\\3 & 4\end{array}\right),\quad \mathbf B=\left(\begin{array}{rr}7 & 2\\9 & 4\end{array}\right),\quad \mathbf C=\left(\begin{array}{rr}-5 & 0\\0 & 2\end{array}\right). \end{gathered} \]
Solution: \[ \begin{aligned} \det \mathbf A & = 1\cdot 4-3\cdot 2=-2,\\ \mathbf A^{-1} & = -\frac{1}{2} \left(\begin{array}{rr}4 & -2\\-3 & 1\end{array}\right) =\left(\begin{array}{rr}-2 & 1\\ 3/2 & -1/2\end{array}\right),\\[5pt] \det\mathbf B & = 7\cdot 4-9\cdot 2=10,\\ \mathbf B^{-1} & =\frac{1}{10}\left(\begin{array}{rr}4 & -2\\-9&7\end{array} \right)=\left(\begin{array}{rr}0.4 & -0.2\\-0.9 & 0.7\end{array}\right),\\[5pt] \det\mathbf C & =(-5)\cdot 2-0=-10,\\ \mathbf C^{-1} & =-\frac{1}{10}\left(\begin{array}{rr}2 & 0\\0 & -5\end{array}\right) =\left(\begin{array}{rr}-0.2 &0\\0 & 0.5\end{array} \right). \end{aligned} \]
We conclude this section with a theorem that formulates further useful and important properties of regular matrices:
Theorem 7.40 Let \(\mathbf A\) and \(\mathbf B\) be two regular matrices of the same order. Then the following always holds: \[ \begin{gathered} (\mathbf A^{-1})^{-1}=\mathbf A,\quad (\mathbf A\cdot \mathbf B)^{-1} = \mathbf B^{-1}\cdot \mathbf A^{-1}, \end{gathered} \] furthermore, for all non-zero real numbers \(\gamma\): \[ \begin{gathered} \left(\gamma\mathbf A\right)^{-1}=\frac{1}{\gamma}\mathbf A^{-1}. \end{gathered} \]
Justification: The first part of the statement is quite clear, the inverse of the inverse is the original matrix. The second claim requires an explanation. If \(\mathbf B^{-1}\mathbf A^{-1}\) is the inverse of \(\mathbf A\cdot\mathbf B\), then it must be: \[ \begin{gathered} \mathbf B^{-1}\mathbf A^{-1}\mathbf A\mathbf B=\mathbf I. \end{gathered} \] Using the associative law: \[ \begin{gathered} \mathbf B^{-1}(\underbrace{\mathbf A^{-1}\mathbf A}_{=\mathbf I})\mathbf B = \mathbf B^{-1}\mathbf B=\mathbf I. \end{gathered} \] This peculiar rule follows naturally from the fact that the commutative law does not apply.
7.4.3 Matrix Equations
In this section, we examine linear equations where the unknown is a matrix. While in the case of numerical equations we are limited to the simple equation \(ax=c\), the variety of forms with matrices is significantly greater. This is mainly because the commutative law generally does not apply to matrices.
Although the circumstances are somewhat more complicated, there are only a few rules that matter when solving these kinds of equations:
The multiplication of matrices is generally not commutative.
We cannot simply divide equations. However, we have the option to multiply equations on both sides by the inverse of a matrix.
The distributive law also applies to matrices.
With these tools, we can now illustrate with specific example problems how to apply these simple rules to solve equations.
Exercise 7.41 Solve the equations \(\mathbf A\mathbf X=\mathbf B\) and \(\mathbf X\mathbf A=\mathbf B\) with: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr}4 & 5\\3 & 4\end{array}\right),\quad \mathbf B=\left(\begin{array}{rr} 9 & -7\\7 & -6\end{array}\right). \end{gathered} \]
Solution: Although these two equations look very similar to each other, they have quite different solutions because the matrix product is not commutative.
We start with the first equation: \[ \begin{gathered} \begin{array}{rclclcl} \mathbf A\mathbf X&=&\mathbf B &&|\rightarrow \times \mathbf A^{-1} &&\text{multiply by $\mathbf A^{-1}$ }\mathit{from the left}\\[5pt] \underbrace{\mathbf A^{-1}\mathbf A}_{=\mathbf I}\mathbf X&=&\mathbf A^{-1}\mathbf B&&&&\mathbf A^{-1}\mathbf A=\mathbf I\;!\\[15pt] \mathbf I\;\mathbf X&=&\mathbf A^{-1}\mathbf B&&&&\mathbf I\;\mathbf X=\mathbf X\\[5pt] \mathbf X&=&\mathbf A^{-1}\mathbf B \end{array} \end{gathered} \] Now we insert the numerical data. First we calculate the inverse of \(\mathbf A\) with the help of Theorem 7.36: \[ \begin{gathered} \det\mathbf A=4\cdot4-3\cdot 5=1,\quad\mathbf A^{-1}=\left(\begin{array}{rr}4 & -5\\-3 & 4\end{array}\right). \end{gathered} \] Now: \[ \begin{gathered} \mathbf X=\mathbf A^{-1}\mathbf B= \left(\begin{array}{rr}4 & -5\\-3 & 4\end{array}\right) \left(\begin{array}{rr}9 & -7\\7 & -6\end{array}\right)= \left(\begin{array}{rr}1 & 2\\1 & -3\end{array}\right). \end{gathered} \] Now to the second equation: \[ \begin{gathered} \begin{array}{rclclcl} \mathbf X\mathbf A&=&\mathbf B &&|\leftarrow \times \mathbf A^{-1} &&\text{multiply by $\mathbf A^{-1}$ }\mathit{from the right}\\[5pt] \mathbf X\underbrace{\mathbf A^{-1}\mathbf A}_{=\mathbf I} &=&\mathbf B\mathbf A^{-1}&&&&\mathbf A^{-1}\mathbf A=\mathbf I\;!\\[20pt] \mathbf X\;\mathbf I&=&\mathbf B\mathbf A^{-1}&&&&\mathbf X\;\mathbf I=\mathbf X\\%[5pt] \mathbf X&=&\mathbf B\mathbf A^{-1} \end{array} \end{gathered} \] We insert the numerical data. We already have \(\mathbf A^{-1}\), so: \[ \begin{gathered} \mathbf X=\mathbf B\mathbf A^{-1}= \left(\begin{array}{rr}9 & -7\\7 & -6\end{array}\right) \left(\begin{array}{rr}4 & -5\\-3 & 4\end{array}\right) = \left(\begin{array}{rr}57 & -73\\46 & -59\end{array}\right). \end{gathered} \] We see that these two equations, as similar as they are to each other, still have fundamentally different solutions, because \(\mathbf A^{-1}\mathbf B\ne \mathbf B\mathbf A^{-1}\). □
Remark 7.42 An important special case, which is covered by Exercise 7.41, occurs when in the equation \(\mathbf A\mathbf X=\mathbf B\) the matrix \(\mathbf X\) has only one column. Then \(\mathbf X\) reduces to a column vector \(\mathbf x\), and the same applies to the right side \(\mathbf B\), which also becomes a column vector. The equation then represents nothing else but a linear system of equations, as we have already noted in 7.7. Therefore, we can also formally solve linear systems of equations with the help of the inverse, provided that the coefficient matrix \(\mathbf A\) is square and regular. In other words: the system of equations has as many equations as unknowns and is uniquely solvable. Formally: \[ \begin{gathered} \mathbf A\mathbf x=\mathbf b\quad|\rightarrow \times \mathbf A^{-1}\\[5pt] \mathbf x=\mathbf A^{-1}\mathbf b \end{gathered} \tag{7.22}\]
Exercise 7.43 Find the solution \(\mathbf X\) to the matrix equation \(\mathbf A\mathbf X +\mathbf B\mathbf X=\mathbf C\) with: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} 8 & -9\\ 1 & 4\\ \end{array}\right), \mathbf B=\left(\begin{array}{rr} 10 & 3\\ -2 & 2\\ \end{array}\right), \mathbf C=\left(\begin{array}{rr} -24 & 18\\ -44 & 50\\ \end{array}\right). \end{gathered} \]
Solution: Here we use the distributive law for the first time. We observe that on the left side of the equation, \(\mathbf X\) appears as a right factor in both products. Therefore, we extract \(\mathbf X\) to the right: \[ \begin{gathered} \begin{array}{rclcl} \mathbf A\mathbf X+\mathbf B\mathbf X&=&\mathbf C && \\[5pt] (\mathbf A+\mathbf B)\mathbf X&=&\mathbf C&&|\rightarrow \times(\mathbf A+\mathbf B)^{-1}\\[5pt] \underbrace{(\mathbf A+\mathbf B)^{-1}(\mathbf A+\mathbf B)}_{=\mathbf I}\mathbf X&=& (\mathbf A+\mathbf B)^{-1}\mathbf C\\[5pt] \mathbf X&=&(\mathbf A+\mathbf B)^{-1}\mathbf C. \end{array} \end{gathered} \] Now we insert the numerical values: \[ \begin{gathered} \mathbf A+\mathbf B= \left(\begin{array}{rr} 8 & -9\\ 1 & 4\\ \end{array}\right)+\left(\begin{array}{rr} 10 & 3\\ -2 & 2\\ \end{array}\right)=\left(\begin{array}{rr}18 & -6\\-1 & 6\end{array}\right),\\[5pt] \det(\mathbf A+\mathbf B)=102,\quad(\mathbf A+\mathbf B)^{-1}=\frac{1}{102}\left(\begin{array}{rr} 6 & 6\\1 & 18 \end{array}\right). \end{gathered} \] Therefore, we obtain: \[ \begin{aligned} \mathbf X&=(\mathbf A+\mathbf B)^{-1}\mathbf C=\frac{1}{102}\left(\begin{array}{rr} 6 & 6\\1 & 18 \end{array}\right)\left(\begin{array}{rr} -24 & 18\\ -44 & 50\\ \end{array}\right)\\[5pt] &=\frac{1}{102}\left(\begin{array}{rr} -408 & 408\\ -816 & 918 \end{array}\right) =\left(\begin{array}{rr}-4 & 4\\-8 & 9\end{array}\right). \end{aligned} \] □
Remark 7.44 We could not have solved the equation \(\mathbf A\mathbf X+\mathbf X\mathbf B=\mathbf C\) in this way, because \(\mathbf X\) appears as a right and as a left factor in the two summands. Therefore, we cannot extract \(\mathbf X\). Specific methods are required for such equations, which we will not delve into here. Just to note, these equations are certainly significant, for instance, in the study of the stability of dynamic systems in mathematical economics.
Exercise 7.45 Find the solution \(\mathbf X\) to the matrix equation \(\mathbf X\mathbf A +\mathbf B=\mathbf X+\mathbf C\) with: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} 5 & -1\\ -2 & 1\\ \end{array}\right), \mathbf B=\left(\begin{array}{rr} 6 & 3\\ -7 & -10\\ \end{array}\right), \mathbf C=\left(\begin{array}{rr} -12 & 12\\ -7 & -11\\ \end{array}\right) \end{gathered} \]
Solution: First, we move \(\mathbf B\) to the right and \(\mathbf X\) to the left: \[ \begin{gathered} \begin{array}{rclcl} \mathbf X\mathbf A+\mathbf B&=&\mathbf X+\mathbf C&&|-\mathbf B-\mathbf X\\[5pt] \mathbf X\mathbf A-\mathbf X&=&\mathbf C-\mathbf B\\[5pt] \mathbf X\mathbf A- \mathbf X\,\mathbf I&=&\mathbf C-\mathbf B \end{array} \end{gathered} \] Now we can extract \(\mathbf X\) to the left on the left side: \[ \begin{gathered} \begin{array}{rclcl} \mathbf X(\mathbf A-\mathbf I)&=&\mathbf C-\mathbf B&&|\leftarrow\times (\mathbf A-\mathbf I)^{-1}\\[5pt] \mathbf X\underbrace{(\mathbf A-\mathbf I)(\mathbf A-\mathbf I)^{-1}}_{=\mathbf I}&=&(\mathbf C-\mathbf B)(\mathbf A-\mathbf I)^{-1}\\[5pt] \mathbf X&=&(\mathbf C-\mathbf B)(\mathbf A-\mathbf I)^{-1}. \end{array} \end{gathered} \] Now the numerical calculation: \[ \begin{gathered} \mathbf A-\mathbf I=\left(\begin{array}{rr} 5 & -1\\ -2 & 1\\ \end{array}\right)-\left(\begin{array}{cc}1 & 0\\0 & 1\end{array}\right)=\left(\begin{array}{rr}4 & -1\\-2 & 0\end{array}\right),\\[5pt] \det(\mathbf A-\mathbf I)=-2,\quad (\mathbf A-\mathbf I)^{-1}= -\frac{1}{2}\left(\begin{array}{rr}0 & 1\\2 & 4\end{array}\right),\\[5pt] \mathbf C-\mathbf B=\left(\begin{array}{rr}-18 & 9\\0 & -1\end{array}\right). \end{gathered} \] Therefore, we obtain: \[ \begin{aligned} \mathbf X&=(\mathbf C-\mathbf B)(\mathbf A-\mathbf I)^{-1} =\left(-\frac{1}{2}\right)\left(\begin{array}{rr}-18 & 9\\0 & -1\end{array}\right) \left(\begin{array}{rr}0 & 1\\2 & 4\end{array}\right)\\[5pt] &=-\frac{1}{2}\left(\begin{array}{rr}18 & 18\\-2 & -4\end{array}\right) =\left(\begin{array}{rr}-9 & -9\\1 & 2\end{array}\right). \end{aligned} \] □
The following matrix equation is important in statistics and econometrics.
Exercise 7.46 Solve the equation \({\mathbf X}^\top \mathbf X\mathbf{\beta}={\mathbf X}^\top \mathbf y\) for \(\mathbf{\beta}\) with: \[ \begin{gathered} \mathbf X=\left(\begin{array}{cc}1 & 2\\1 & 4\end{array}\right),\quad \mathbf y=\left(\begin{array}{r}5\\11\end{array}\right). \end{gathered} \]
Solution: The formal solution to this equation is simple: we multiply from the left by the inverse of \({\mathbf X}^\top \mathbf X\): \[ \begin{gathered} \begin{array}{rclcl} {\mathbf X}^\top \mathbf X\mathbf{\beta}&=&{\mathbf X}^\top \mathbf y&&|\rightarrow ({\mathbf X}^\top \mathbf X)^{-1}\\[5pt] \mathbf{\beta}&=&({\mathbf X}^\top \mathbf X)^{-1}\,{\mathbf X}^\top \mathbf y. \end{array} \end{gathered} \] Now the calculation: \[ \begin{gathered} {\mathbf X}^\top =\left(\begin{array}{rr}1 & 1\\2 & 4\end{array}\right),\quad {\mathbf X}^\top \mathbf X=\left(\begin{array}{rr}1 & 1\\2 & 4\end{array}\right)\left(\begin{array}{cc}1 & 2\\1 & 4\end{array}\right) =\left(\begin{array}{rr}2 & 6\\6 & 20 \end{array}\right),\\[5pt] {\mathbf X}^\top \mathbf y=\left(\begin{array}{rr}1 & 1\\2 & 4\end{array}\right)\left(\begin{array}{r}5\\11\end{array}\right) =\left(\begin{array}{r}16\\54\end{array}\right). \end{gathered} \] Furthermore: \[ \begin{gathered} \det({\mathbf X}^\top \mathbf X)=4,\quad ({\mathbf X}^\top \mathbf X)^{-1}=\frac{1}{4} \left(\begin{array}{rr}20 & -6\\-6 & 2\end{array}\right). \end{gathered} \] And hence: \[ \begin{aligned} \mathbf{\beta}&=({\mathbf X}^\top \mathbf X)^{-1}\,{\mathbf X}^\top \mathbf y \\[5pt] &=\frac{1}{4} \left(\begin{array}{rr}20 & -6\\-6 & 2\end{array}\right) \left(\begin{array}{r}16\\54\end{array}\right)= \frac{1}{4}\left(\begin{array}{r}-4\\12\end{array}\right)= \left(\begin{array}{r}-1\\3\end{array}\right). \end{aligned} \] □
Exercise 7.47 Find the solution \(\mathbf X\) to the matrix equation \(\mathbf A^{-1}\mathbf X\mathbf B=\mathbf C\) with: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} 2 & 1\\ -1 & 5\\ \end{array}\right), \quad\mathbf B=\left(\begin{array}{rr} 4 & 11\\ 1 & 3\\ \end{array}\right), \quad\mathbf C=\left(\begin{array}{rr} 1 & 0\\ 3 & -4\\ \end{array}\right). \end{gathered} \]
Solution: First, we multiply both sides of the equation from the left by \(\mathbf A\): \[ \begin{gathered} \mathbf A^{-1}\mathbf X\mathbf B=\mathbf C\qquad|\rightarrow\times \mathbf A\\[5pt] \underbrace{\mathbf A\mathbf A^{-1}}_{=\mathbf I}\mathbf X\mathbf B=\mathbf A\mathbf C\\[5pt] \mathbf X\mathbf B=\mathbf A\mathbf C. \end{gathered} \] Next, we multiply both sides of the equation from the right with the inverse of \(\mathbf B\): \[ \begin{gathered} \mathbf X\mathbf B=\mathbf A\mathbf C\qquad| \leftarrow \times \mathbf B^{-1}\\[5pt] \mathbf X\underbrace{\mathbf B\mathbf B^{-1}}_{=\mathbf I}= \mathbf A\mathbf C\mathbf B^{-1}\\[5pt] \mathbf X=\mathbf A\mathbf C\mathbf B^{-1}. \end{gathered} \] Now we substitute in the numerical values: \[ \begin{aligned} \mathbf B^{-1}&=\left(\begin{array}{rr}3 & -11\\-1 & 4\end{array}\right),\\[5pt] \mathbf X&=\mathbf A\mathbf C\mathbf B^{-1}\\[5pt] &= \left(\begin{array}{rr} 2 & 1\\ -1 & 5\\ \end{array}\right)\left(\begin{array}{rr} 1 & 0\\ 3 & -4\\ \end{array}\right)\left(\begin{array}{rr}3 & -11\\-1 & 4\end{array}\right) = \left(\begin{array}{rr} 19 & -71\\ 62 &-234 \end{array}\right). \end{aligned} \] □
Exercise 7.48 Find the solution \(\mathbf X\) to the matrix equation \(\mathbf A{\mathbf X}^\top +\mathbf B=\mathbf C\) with: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} 7 & -1\\ 7 & -3\\ \end{array}\right), \quad\mathbf B=\left(\begin{array}{rr} 9 & 1\\ 10 & -2\\ \end{array}\right), \quad\mathbf C=\left(\begin{array}{rr} -43 & -50\\ -34 & -57\\ \end{array}\right). \end{gathered} \]
Solution: We move \(\mathbf B\) to the right side and then multiply by the inverse of \(\mathbf A\) from the left: \[ \begin{gathered} \begin{array}{rclcl} \mathbf A{\mathbf X}^\top +\mathbf B&=&\mathbf C&&|-\mathbf B\\[5pt] \mathbf A{\mathbf X}^\top &=&\mathbf C-\mathbf B&&|\rightarrow\times \mathbf A^{-1}\\[5pt] \underbrace{\mathbf A^{-1}\mathbf A}_{=\mathbf I}{\mathbf X}^\top &=& \mathbf A^{-1}(\mathbf C-\mathbf B)\\[5pt] {\mathbf X}^\top &=&\mathbf A^{-1}(\mathbf C-\mathbf B). \end{array} \end{gathered} \] But, how do we proceed? Quite simple, we recall Definition 7.3: the transpose of the transpose is the original matrix, that is \({({\mathbf X}^\top )}^\top = \mathbf X\). Therefore, we transpose both sides of the equation and obtain the formal solution: \[ \begin{gathered} \mathbf X={(\mathbf A^{-1}(\mathbf C-\mathbf B))}^\top. \end{gathered} \] Now we substitute: \[ \begin{gathered} \det\mathbf A=-14,\quad \mathbf A^{-1}=-\frac{1}{14}\left( \begin{array}{rr}-3 & 1\\-7 & 7\end{array}\right),\quad \mathbf C-\mathbf B=\left( \begin{array}{rr} -52 & -51\\ -44 & -55 \end{array}\right). \end{gathered} \] Therefore: \[ \begin{aligned} \mathbf A^{-1}(\mathbf C-\mathbf B)&=-\frac{1}{14} \left(\begin{array}{rr}-3 & 1\\-7 & 7\end{array}\right)\left( \begin{array}{rr} -52 & -51\\ -44 & -55 \end{array}\right)=-\frac{1}{14}\left(\begin{array}{rr} 112 & 98\\ 56 & -28 \end{array}\right)\\[5pt] &=\left(\begin{array}{rr} -8 & -7\\ -4 & 2 \end{array} \right)={\mathbf X}^\top . \end{aligned} \] Thus, we get: \[ \begin{gathered} \mathbf X =\left(\begin{array}{rr} -8 & -7\\ -4 & 2 \end{array} \right)^{\textsf T}=\left(\begin{array}{rr} -8 & -4\\-7 & 2\end{array}\right). \end{gathered} \] □
7.5 Input-Output Analysis
Input-Output Analysis is a famous application of matrix calculation in economics. It originated in the research of Wassily Leontief2 on the theory of General Market Equilibrium. The central question is: what equilibrium forms in a system of markets that are intricately interconnected by supply and service flows.
The Input-Output Model developed by Leontief is used to quantitatively describe the relationships between the sectors of an economy. However, the Input-Output Model can also be used to describe the exchange of services between parts of a production company. The Method of Internal Transfer Pricing, which we have discussed among others in Example 6.7, is very similar to the Leontieff Model.
However, we will only consider an economic interpretation of the Input-Output Model here.
7.5.1 An introductory example
An economy consists of three sectors: agriculture, livestock farming, and industry. Agriculture produces wheat, livestock farming produces pigs, and industry produces iron. The three sectors supply each other and maintain production. In addition, they produce surpluses for final consumption (private or public consumption).
In detail:
- Agriculture produces \(450\,q\) of wheat and requires \(200\,q\) of wheat, \(7\,t\) of iron, and 18 pigs for this purpose.
- The industry produces \(21\,t\) of iron and requires \(90\,q\) of wheat, \(6\,t\) of iron, and 12 pigs for this purpose.
- Livestock farming produces 60 pigs and requires \(120\,q\) of wheat, \(3\,t\) of iron, and 15 pigs for this purpose.
These three economic sectors produce surpluses: agriculture generates a surplus of \(40\,q\) of wheat, industry of \(5\,t\) of iron, livestock farming of 15 pigs. These surpluses are available for final consumption.
If we break down the produced quantities by their use, we obtain the following picture:
\[ \begin{array}{|l|ccccccccc|} \hline & \text{Use} && \text{Agriculture} && \text{Industry} && \text{Livestock} && \text{Final}\\ & \text{by} && && && \text{Farming} &&\text{Consumption}\\ \hline \text{Wheat} &450&=&200&+&90&+&120&+&40\\ \text{Iron} &21&=&7&+&6&+&3&+&5\\ \text{Pigs} &60&=&18&+&12&+&15&+&15\\ \hline \end{array} \]
This table is called the Input-Output Table.
The Input-Output Table is often written in the following form:
\[ \begin{array}{|l|cccc|} \hline \text{Delivery} & \text{to Sector 1} & \text{to Sector 2} & \text{to Sector 3} & \text{Final Consumption}\\ \hline \text{from Sector 1} &200&90&120&40\\ \text{from Sector 2} &7&6&3&5\\ \text{from Sector 3} &18&12&15&15\\ \hline \end{array} \]
The row sums of the Input-Output Table give the total output of the respective sector. The vectors of all outputs and all deliveries to final consumption \[ \begin{gathered} \mathbf x=\left(\begin{array}{r}450\\21\\60 \end{array}\right),\quad \mathbf b=\left(\begin{array}{r}40\\5\\15 \end{array}\right) \end{gathered} \] are called the Output Vector and Final Consumption Vector.
Let’s now determine the requirement vectors for each sector. The requirement vectors contain the quantities of inputs needed to produce one unit of the respective product. The requirement vector of a sector is obtained by dividing the vector of deliveries to a sector by the output of the sector. The requirement vectors are evidently: \[ \begin{gathered} \renewcommand{\arraystretch}{1.5} \begin{array}{ccc} \mbox{Agriculture} & \mbox{Industry} & \mbox{Livestock} \\ \left(\begin{array}{c}\frac{200}{450}\\\frac{7}{450}\\\frac{18}{450} \end{array}\right)& \left(\begin{array}{c}\frac{90}{210}\\\frac{6}{210}\\\frac{12}{210} \end{array}\right)& \left(\begin{array}{c}\frac{120}{60}\\\frac{3}{60}\\\frac{15}{60} \end{array}\right). \end{array} \end{gathered} \] If one compiles these requirement vectors into a matrix, this resulting requirement matrix is called the technology matrix. In our example, it is: \[ \begin{gathered} \mathbf A= \renewcommand{\arraystretch}{1.5} \left(\begin{array}{ccc} \frac{200}{450}&\frac{90}{210}&\frac{120}{60}\\ \frac{7}{450}&\frac{6}{210}&\frac{3}{60}\\ \frac{18}{450}&\frac{12}{210}&\frac{15}{60} \end{array}\right) = \left(\begin{array}{rrr} 0.4444&4.2857&2.0000\\ 0.0156&0.2857&0.0500\\ 0.0400&0.5714&0.2500 \end{array}\right). \end{gathered} \] In order to produce output \(\mathbf x\), the economy needs the quantity \(\mathbf A\mathbf x\) as input. Thus, \(\mathbf A\mathbf x\) is the input vector required for the output \(\mathbf x\). The original input-output table is then equivalent to the matrix equation \[ \begin{gathered} \renewcommand{\arraystretch}{1.5} \left(\begin{array}{c}450\\210\\60\end{array}\right)= \left(\begin{array}{ccc} \frac{200}{450}&\frac{90}{210}&\frac{120}{60}\\ \frac{7}{450}&\frac{6}{210}&\frac{3}{60}\\ \frac{18}{450}&\frac{12}{210}&\frac{15}{60} \end{array}\right) \cdot \left(\begin{array}{r}450\\210\\60\end{array}\right)+ \left(\begin{array}{r}40\\5\\15\end{array}\right) \end{gathered} \] This equation is called the input-output equation and has the symbolic form \[ \begin{gathered} \mathbf x=\mathbf A\mathbf x+\mathbf b. \end{gathered} \] It means that the difference between the produced output \(\mathbf x\) and the required input \(\mathbf A\mathbf x\) is delivered to the final consumer.
7.5.2 Basic Concepts
We now proceed to describe the situation presented in the example in general terms.
An economy consists of three sectors. We denote with
\[ \begin{array}{rl} x_1: & \text{Output quantity of sector 1,} \\ x_2: & \text{Output quantity of sector 2,} \\ x_3: & \text{Output quantity of sector 3.} \end{array} \]
The sectors depend on each other. They supply each other and they supply the final consumer.
\[ \begin{array}{rl} x_{ij}: & \text{Delivery from sector $i$ to sector $j$,} \\ b_i: & \text{Delivery from sector $i$ to the final consumer.} \end{array} \]
The input-output table is a system of equations that breaks down the output quantities by their use: \[ \begin{gathered} \begin{array}{|l|rcccccccc|} \hline &\text{Used by} && \text{Sector} && \text{Sector} && \text{Sector} && \text{Final} \\ & && \text{1} && \text{2} && \text{3} && \text{consumption}\\ \hline \text{Sector 1}&x_1 & = & x_{11} &+& x_{12} &+& x_{13} &+& b_1\\ \text{Sector 2}&x_2 & = & x_{21} &+& x_{22} &+& x_{23} &+& b_2\\ \text{Sector 3}&x_3 & = & x_{31} &+& x_{32} &+& x_{33} &+& b_3\\ \hline \end{array} \end{gathered} \tag{7.23}\] If you abbreviate this system of equations by writing only the coefficient matrix, you get the input-output matrix \[ \begin{gathered} \begin{array}{|l|cccc|c|} \hline \text{Deliveries} & &\text{to Sector 1}&\text{to Sector 2}&\text{to Sector 3}&\text{Final Consumption}\\ \hline \text{from Sector 1} && x_{11} & x_{12} & x_{13} & b_1\\ \text{from Sector 2} && x_{21} & x_{22} & x_{23} & b_2\\ \text{from Sector 3} && x_{31} & x_{32} & x_{33} & b_3\\ \hline \end{array} \end{gathered} \tag{7.24}\] The row sums of the input-output table yield the total output of the respective sector: \[ \begin{gathered} x_i=x_{i1}+x_{i2}+x_{i3}+b_i,\;i=1,2,3. \end{gathered} \tag{7.25}\] Starting from an input-output table, one first has to compute the technology matrix. This is done as follows: To produce a unit of its product, the economic sector \(j\) requires exactly \[ \begin{gathered} a_{ij}:=\frac{x_{ij}}{x_{j}} \end{gathered} \tag{7.26}\] units of products from the economic sector \(i\).
We compile these sizes into a matrix: \[ \begin{gathered} \mathbf A= \left( \begin{array}{rrr} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right). \end{gathered} \] This demand matrix is the aforementioned Technology matrix or Leontief matrix. It arises by dividing the columns of the input-output matrix by the row sums. The technology matrix \(\mathbf A\) reflects the technological state of the economy.
7.5.3 The Input-Output Equation
To produce \(x_j\) units, sector \(j\) therefore needs a supply of \(x_{ij}=a_{ij}x_j\) units from sector \(i\). The equation system of the input-output table now takes the form
\[ \begin{gathered} \begin{array}{rcrcrcrcr} x_1 &=& a_{11}x_1 &+& a_{12}x_2 &+& a_{13}x_3 &+& b_1 \\ x_2 &=& a_{21}x_1 &+& a_{22}x_2 &+& a_{23}x_3 &+& b_2 \\ x_3 &=& a_{31}x_1 &+& a_{32}x_2 &+& a_{33}x_3 &+& b_3 \end{array} \end{gathered} \tag{7.27}\] In matrix notation, this system of equations reads \(\mathbf x=\mathbf A\mathbf x+\mathbf b\).
Definition 7.49 Let \(\mathbf A\) be an \(n\times n\) matrix with nonnegative components and let \(\mathbf b\in \mathbb R^n\) be a vector, also with nonnegative components. Then the matrix equation \[ \begin{gathered} \mathbf x=\mathbf A\mathbf x+\mathbf b \end{gathered} \tag{7.28}\] is called the input-output equation.
7.5.4 Static Equilibrium
The input-output equation (7.28) is not very interesting in itself; it is a balance relationship. However, if we consider how the quantities in the equation can change over time, we find that the technology matrix is short-term immutable. It represents the production function used by an economy, reflecting its technological state of development. Only in the medium and long term will \(\mathbf A\) change under the influence of technical progress.
On the other hand, output and final consumption are short-term variable quantities. Therefore, knowing the technology matrix, one can attempt to find other solutions \(\mathbf x\) and \(\mathbf b\) to the input-output equation \(\mathbf x=\mathbf A\mathbf x+\mathbf b\) with unchanged \(\mathbf A\). The main question that arises is:
- How must the output vector \(\mathbf x\) be chosen to enable a certain final consumption \(\mathbf b\)?
The answer to this question is given by the following theorem.
Theorem 7.50 Let \(\mathbf A\) be a technology matrix with the property that the matrix \(\mathbf I-\mathbf A\) is regular and \((\mathbf I-\mathbf A)^{-1}\) has only nonnegative elements.
Then for every final consumption \(\mathbf b\) there is a uniquely determined output vector \(\mathbf x\) that solves the input-output equation \(\mathbf x=\mathbf A\mathbf x+\mathbf b\). It is given by \[ \begin{gathered} \mathbf x=(\mathbf I-\mathbf A)^{-1}\mathbf b. \end{gathered} \tag{7.29}\]
Explanation: We solve this matrix equation as discussed in Section 7.4.3: \[ \begin{aligned} \mathbf x &=\mathbf A\mathbf x+\mathbf b \\ &\Rightarrow \mathbf x-\mathbf A\mathbf x =\mathbf b &\Rightarrow\; (\mathbf I-\mathbf A)\mathbf x=\mathbf b &&\Rightarrow\; \mathbf x=(\mathbf I-\mathbf A)^{-1}\mathbf b. \end{aligned} \] □
An input-output model for Austria from the year 1955 includes the economic sectors 1. Enterprises, 2. Public sector, 3. Foreign countries. The final consumption is caused by private households. The input-output table is (in billion Schillings)
\[ \begin{array}{|l|cccc|} \hline \text{Delivery} &\text{to Sector 1} &\text{to Sector 2} &\text{to Sector 3} &\text{Final consumption}\\ \hline \text{from Sector 1} &-&16.4&25.8&76.9\\ \text{from Sector 2} &14.3&-&-&11.6\\ \text{from Sector 3} &22.1&0.7&-&-\\ \hline \end{array} \]
The output vector (row sums) is \[ \begin{gathered} \mathbf x=\left(\begin{array}{r}119.1\\25.9\\22.8\end{array}\right). \end{gathered} \] The technology matrix is calculated by dividing the first three columns of the table by the row sums of the table: \(a_{ij}=\frac{x_{ij}}{x_j}.\) This yields \[ \begin{gathered} \mathbf A=\left(\begin{array}{rrr}0& 0.6332& 1.1316\\ 0.1201&0&0\\0.1856&0.0270&0 \end{array}\right). \end{gathered} \] The input-output equation thus takes the form \[ \begin{aligned} &\left(\begin{array}{r}119.1\\25.9\\22.8\end{array}\right)=\\ &\left(\begin{array}{rrr}0& 0.6332& 1.1316\\ 0.1201&0&0\\0.1856&0.0270&0 \end{array}\right)\cdot \left(\begin{array}{r}119.1\\25.9\\22.8\end{array}\right)+ \left(\begin{array}{r}76.9\\11.6\\0.0\end{array}\right). \end{aligned} \] Using a computer program, we invert the matrix \(\mathbf I-\mathbf A\): \[ \begin{gathered} (\mathbf I-\mathbf A)^{-1}= \left(\begin{array}{lll} 1.4078 & 0.9345 & 1.5930 \\ 0.1690 & 1.1122 & 0.1913 \\ 0.2658 & 0.2035 & 1.3008 \end{array}\right). \end{gathered} \] Suppose we wanted to increase the deliveries from sector 1 (enterprises) to final demand to 80 billion and the deliveries from sector 2 (public sector) to 15 billion, i.e., the final demand vector should be \[ \begin{gathered} \mathbf b=\left(\begin{array}{r}80\\15\\0\end{array}\right) \end{gathered} \] then the output of all three sectors would have to be \[ \begin{aligned} \mathbf x & =(\mathbf I-\mathbf A)^{-1}\mathbf b \\ & =\left(\begin{array}{lll} 1.4078 & 0.9345 & 1.5930 \\ 0.1690 & 1.1122 & 0.1913 \\ 0.2658 & 0.2035 & 1.3008 \end{array}\right) \left(\begin{array}{r}80\\15\\0\end{array}\right)= \left(\begin{array}{r}126.64\\30.21\\24.32\end{array}\right) \end{aligned} \]
Exercise 7.52 A conglomerate consists of the divisions Mining (R), Steel Production (S), and Trading Companies (H). The divisions supply each other but also sell independently. The following table contains the deliveries (in million currency units) for the three divisions:
\[ \begin{gathered} \begin{array}{r|rrr|c} & \text{to R}& \text{to S} & \text{to H} & \text{Sale}\\ \hline R & 0& 250& 100& 100\\ S & 50 &0 &250 &350\\ H &100 &150 &0 &250\\ \hline \end{array} \end{gathered} \]
What is the output of the three divisions?
What is the technology matrix?
How must the output change if sales in the Steel Production and Trading Companies divisions are to be increased by \(10\%\)?
Solution:
(a) The row sums of the input-output: \[ \begin{gathered} \mathbf{x} = \left( {\begin{array}{r} 450 \\ 650 \\ 500 \\ \end{array} }\right) = \begin{array}{l} \text{Output of R} \\ \text{Output of S} \\ \text{Output of H} \\ \end{array} \end{gathered} \]
(b) We obtain the technology matrix by dividing the columns of the input-output table by the corresponding components of the output vector: \[ \begin{gathered} \renewcommand{\arraystretch}{1.5} \mathbf A=\left(\begin{array}{ccc} \frac{0}{450} &\frac{250}{650}& \frac{100}{500}\\ \frac{50}{450}& \frac{0}{650}& \frac{250}{500}\\ \frac{100}{450}& \frac{150}{650}& \frac{0}{500} \end{array}\right) = \left(\begin{array}{rrr} 0.0000 & 0.3846 & 0.2000 \\ 0.1111 & 0.0000 & 0.5000 \\ 0.2222 & 0.2308 & 0.0000 \end{array} \right). \end{gathered} \]
(c) An increase of 10% in the sales of S and H for the final consumption vector means: \[ \begin{gathered} \mathbf{b} = \left( \begin{array}{c} 100 \\ 350 + 35 \\ 250 + 25 \end{array} \right) = \left( \begin{array}{r} 100 \\ 385 \\ 275 \end{array} \right). \end{gathered} \]
We need to calculate \(\mathbf x=(\mathbf I-\mathbf A)^{-1}\mathbf b\): \[ \begin{aligned} \mathbf{I}-\mathbf{A} &=& \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right) - \left( \begin{array}{rrr} 0.0000 & 0.3846 & 0.2000 \\ 0.1111 & 0.0000 & 0.5000 \\ 0.2222 & 0.2308 & 0.0000 \end{array} \right)\\ \\ & =& \left( \begin{array}{rrr} 1.0000 & -0.3846 & -0.2000 \\ -0.1111 & 1.0000 & -0.5000 \\ -0.2222 & -0.2308 & 1.0000 \\ \end{array} \right). \end{aligned} \] The inverse (calculated with a spreadsheet program, for example) is: \[ \begin{gathered} (\mathbf{I}-\mathbf{A})^{-1} = \left( \begin{array}{rrr} 1.1802 & 0.5747 & 0.5234 \\ 0.2965 & 1.2748 & 0.6967 \\ 0.3307 & 0.4219 & 1.2771 \end{array} \right). \end{gathered} \] Finally, we obtain: \[ \begin{aligned} (\mathbf{I}-\mathbf{A})^{-1}\cdot\mathbf{b} &= \left( \begin{array}{rrr} 1.1802 & 0.5747 & 0.5234 \\ 0.2965 & 1.2748 & 0.6967 \\ 0.3307 & 0.4219 & 1.2771 \end{array} \right)\cdot \left( \begin{array}{r} 100 \\ 385 \\ 275 \end{array} \right) \\ &= \left( \begin{array}{r} 483.2145 \\ 712.0405 \\ 546.7040 \end{array} \right). \end{aligned} \] The result is interesting. To achieve the new sales targets in the areas S and H (+10%), all three areas must increase their output, even if to different extents: \[ \begin{gathered} \begin{array}{cccccr} \text{R:} & 450 & \to & 483.2 & = & + 7.4\,\%\\[3pt] \text{S:} & 650 & \to & 712.0 & = & + 9.5\,\%\\[3pt] \text{H:} & 500 & \to & 546.7 & = & + 9.3\,\% \end{array} \end{gathered} \] □
7.6 Additional Exercises
-
Given \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} 5 & -8\\ 1 & -6\\ \end{array}\right),\quad \mathbf B=\left(\begin{array}{rr} -1 & 1\\ -7 & 8\\ \end{array}\right),\quad \mathbf C=\left(\begin{array}{rr} 10 & -1\\ -4 & -7\\ \end{array}\right). \end{gathered} \] Calculate the product \(\mathbf Z=\mathbf A(\mathbf B+\mathbf C)\).
Solution: \(\displaystyle \mathbf Z=\left(\begin{array}{rr} 133 & -8\\ 75 & -6\\ \end{array}\right)\)
-
Given \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} -6 & -1\\ -5 & 4\\ \end{array}\right),\quad \mathbf B=\left(\begin{array}{rr} -10 & -4\\ 8 & 4\\ \end{array}\right). \end{gathered} \] Calculate the product \(\mathbf Z=(\mathbf A+\mathbf B)^2\).
Solution: \(\displaystyle \mathbf Z=\left(\begin{array}{rr} 241 & 40\\ -24 & 49 \end{array}\right)\).
-
Calculate the unknown \(\alpha\) from the matrix product \[ \begin{gathered} \left(\begin{array}{rrr} 3 & -5 & \alpha\\ -2 & -4 & 7\\ \end{array}\right)\cdot \left(\begin{array}{rrr} 5 & 4 & 4\\ 5 & 8 & 2\\ 7 & -9 & 8\\ \end{array}\right)=\left(\begin{array}{rrr} 46 & -100 & 66\\ 19 & -103 & 40\\ \end{array}\right). \end{gathered} \]
Solution: \(\alpha=8\).
-
Determine the constant \(\alpha\) such that the following equation is satisfied: \[ \begin{gathered} \left(\begin{array}{cc}1 & 3 \end{array}\right)\left(\begin{array}{rr} 7 & -4\\ 3 & \alpha\end{array}\right) \left(\begin{array}{r} -2 \\ 4\end{array}\right)=0. \end{gathered} \]
Solution: \(\alpha=4\).
-
In a manufacturing process, the final products \(E_{1}\) and \(E_{2}\) are produced from initial products \(A_{1}\), \(A_{2}\), and \(A_{3}\). Two types of intermediate products are generated, and there are 3 processing stages. The process schema is as follows:
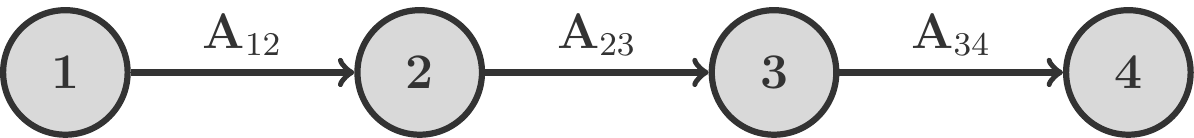
The corresponding demand matrices are: \[ \begin{gathered} \mathbf A_{12}=\left(\begin{array}{rr} 4 & 3\\ 8 & 1\\ 10 & 2\\ \end{array}\right),\quad\mathbf A_{23}=\left(\begin{array}{rr} 10 & 5\\ 4 & 9\\ \end{array}\right), \quad\mathbf A_{34}=\left(\begin{array}{rr} 6 & 6\\ 2 & 6\\ \end{array}\right). \end{gathered} \] A specific delivery order requires that 17 and 3 units of the final products be delivered. What is the demand for the initial products?
Solution: \({\mathbf a}^\top =(8684, 12628, 16496)\).
-
In a company, products \(P_1\), \(P_2\) and \(P_3\) are produced using two machines \(M_1\) and \(M_2\). The required machine times per piece (in minutes) and machine costs are given in the following table:
\[ \begin{array}{|c|rrr|r|} \hline & P_1 & P_2 & P_3 & \text{Costs/Hour}\\ \hline M_1 & 3 & 5 & 1 & 300\qquad\enspace\\ M_2 & 2 & 7 & 6 & 270\qquad\enspace\\ \hline \end{array} \]
An order requires the delivery of 340 units of \(P_1\), 360 units of \(P_2\), and 100 units of \(P_3\). Calculate the total costs of this order.
Solution: 31 700
-
A manufacturer produces two products \(B_1\) and \(B_2\). He needs raw materials \(A_1, A_2\) and \(A_3\). The production takes place in two different factories \(S_1\) and \(S_2\), where different raw material prices prevail. The demand for raw materials and their prices in \(S_1\) and \(S_2\) are given by:
\[ \begin{array}{|l|rr|rr|} \hline &\text{Product} &&\text{Prices in} & \\ & B_1 & B_2 & S_1 & S_2\\ \hline A_1 & 64& 48& 10& 15\\ A_2 & 53 &13 &19 &21\\ A_3 &79&61 &16 &21\\ \hline \end{array} \]
An order requires the delivery of 60 pieces of \(B_1\) and 50 pieces of \(B_2\). Calculate how much higher the total production costs of this order are in \(S_2\) than in \(S_1\).
Solution: 77 810
-
In a manufacturing process, intermediate products \(P_1\) and \(P_2\) are produced from raw materials \(A_1\) and \(A_2\), and from these, further intermediates \(Q_1\) and \(Q_2\) and finally the final products \(E_1\) and \(E_2\). Some of the intermediates \(P_1\) and \(P_2\) also flow directly into the final assembly. The process can be schematically represented as follows:
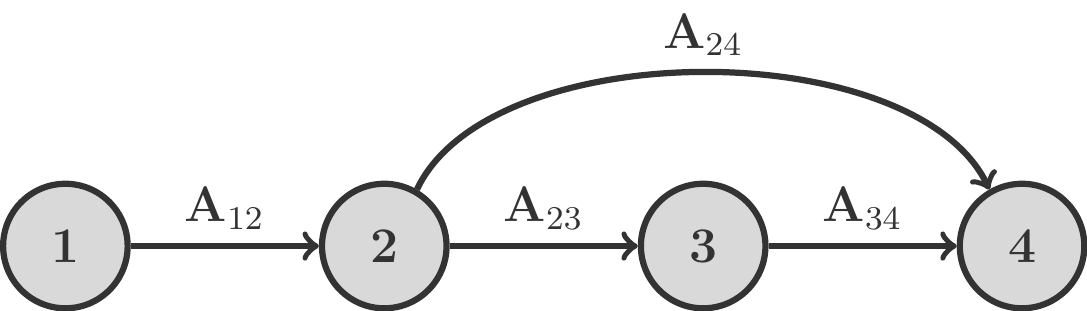
The scale structures of the process sections are represented by the following demand matrices: \[ \begin{gathered} \mathbf A_{12}=\left(\begin{array}{cc}1 & 0\\0 & 4\end{array}\right), \mathbf A_{23}=\left(\begin{array}{cc}2 & 1\\1 & 1\end{array}\right),\\ \mathbf A_{34}=\left(\begin{array}{cc}1 & 1\\0 & 2\end{array}\right), \mathbf A_{24}=\left(\begin{array}{cc}0 & 1\\2 & 0\end{array}\right). \end{gathered} \] If one unit of both \(E_1\) and \(E_2\) is to be produced, how much of \(A_1\) and \(A_2\) is required?
Solution: \(A_1=7, A_2=24\).
-
Calculate the inverse of the matrix \(\displaystyle\mathbf A= \frac{1}{5}\left(\begin{array}{rr}3 & -4\\4 & 3\end{array}\right)\).
Solution: \(\displaystyle\mathbf A^{-1}={\mathbf A}^\top = \frac{1}{5}\left(\begin{array}{rr}3 & 4\\-4 & 3\end{array}\right)\).
-
Calculate the inverse of the matrix \(\mathbf A=\left(\begin{array}{rr} -4 & 15\\-1 & 4\end{array}\right)\).
Solution: \(\mathbf A^{-1}=\mathbf A\), therefore \(\mathbf A^2=\mathbf I\).
-
Given are the column vectors \[ \begin{gathered} \mathbf a=\left(\begin{array}{r}-1\\2\\1\end{array}\right),\quad \mathbf b=\left(\begin{array}{r}4\\2\\0\end{array}\right) \end{gathered} \] Calculate \({\mathbf a}^\top \mathbf b\) and \(\mathbf G=\mathbf a{\mathbf b}^\top\). What is \(\mathbf G^2\)?
Solution: \({\mathbf a}^\top \mathbf b=0\), \[ \begin{gathered} \mathbf G=\left(\begin{array}{rrr} -4 &-2 & 0\\ 8 & 4 & 0\\ 4 & 2 & 0 \end{array}\right),\quad \mathbf G^2=\left(\begin{array}{rrr} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right). \end{gathered} \]
-
For which value of \(\alpha\) is \(\displaystyle \mathbf A= \left(\begin{array}{rr}4 & -2\\3 & \alpha\end{array}\right)\) singular?
Solution: \(\alpha=-3/2\).
-
Given is the matrix \[ \mathbf A = \left(\begin{array}{rr} 1 & 1\\ -1 & 1\\ \end{array}\right). \] Which of the following statements are correct?
The determinant is \(2\).
This matrix does not have an inverse.
The inverse of \(\mathbf A\) is: \[ \mathbf A^{-1}=\frac{1}{2}\left(\begin{array}{rr} 1 & -1\\ 1 & 1\\ \end{array}\right). \]
Solution: (1) and (3)
-
Find the solution \(\mathbf X\) to the matrix equation \(\mathbf X\mathbf A + \mathbf B = \mathbf C\) with: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} -7 & -8\\ 6 & -4\\ \end{array}\right), \mathbf B=\left(\begin{array}{rr} -10 & 9\\ -5 & 6\\ \end{array}\right), \mathbf C=\left(\begin{array}{rr} -37 & -11\\ 21 & -62\\ \end{array}\right). \end{gathered} \]
Solution: \(\displaystyle \mathbf X=(\mathbf C-\mathbf B)\mathbf A^{-1}=\left(\begin{array}{rr} 3 & -1\\ 4 & 9\\ \end{array}\right)\)
-
Find the solution \(\mathbf X\) to the matrix equation \(\mathbf X\mathbf A +\mathbf X\mathbf B=\mathbf C\) with: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} 3 & 2\\ -7 & -2\\ \end{array}\right), \mathbf B=\left(\begin{array}{rr} 4 & 4\\ 9 & -5\\ \end{array}\right), \mathbf C=\left(\begin{array}{rr} -58 & -41\\ 43 & 2\\ \end{array}\right). \end{gathered} \]
Solution: \(\displaystyle \mathbf X=\mathbf C(\mathbf A+\mathbf B)^{-1}=\left(\begin{array}{rr} -8 & -1\\ 5 & 4\\ \end{array}\right)\)
-
Find the solution \(\mathbf X\) to the matrix equation \(\mathbf A\mathbf X +\mathbf B=\mathbf X+\mathbf C\) with: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} -1 & -6\\ 4 & 2\\ \end{array}\right), \mathbf B=\left(\begin{array}{rr} -1 & 8\\ -4 & 5\\ \end{array}\right), \mathbf C=\left(\begin{array}{rr} -11 & 56\\ -28 & 19\\ \end{array}\right). \end{gathered} \]
Solution: \(\displaystyle\mathbf X=(\mathbf A-\mathbf I)^{-1}(\mathbf C-\mathbf B)=\left(\begin{array}{rr} -7 & 6\\ 4 & -10\\ \end{array}\right)\)
-
Find the solution \(\mathbf X\) to the matrix equation \(\mathbf A^{-1}\mathbf X \mathbf B^{-1}=\mathbf I\) with: \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} 4 & -1\\ 2 & 5\\ \end{array}\right), \quad\mathbf B=\left(\begin{array}{rr} -1 & 0\\ 2 & 1\\ \end{array}\right). \end{gathered} \]
Solution: \(\displaystyle \mathbf X=\mathbf A\mathbf B=\left(\begin{array}{rr} -6 & -1\\8 & 5\end{array}\right)\)
-
Find the solution \(\mathbf X\) to the matrix equation \(\mathbf A\mathbf X+\mathbf A\mathbf X\mathbf B=\mathbf C\) with the following data \[ \begin{gathered} \mathbf A=\left(\begin{array}{rr} 2 & 3\\ -1 & -1\\ \end{array}\right), \quad\mathbf B=\left(\begin{array}{rr} 0 & 4\\ 2 & 0\\ \end{array}\right),\quad \mathbf C=\left(\begin{array}{rr} 8 & 11\\ -3 & -5\\ \end{array}\right). \end{gathered} \]
Solution: \(\displaystyle \mathbf X=\mathbf A^{-1}\mathbf C(\mathbf I+\mathbf B)^{-1}=\left(\begin{array}{cc}1 & 0\\0 & 1\end{array}\right)\).
-
An automotive corporation consists of three divisions: the production of passenger cars (P), the production of commercial vehicles (N) and a center for research and development (R&D). The following table presents the flows of deliveries and services within the company as well as the sales of the three divisions (all figures in million currency units, GE):
\[ \begin{array}{|c|rrr|r|r|} \hline \text{Deliveries from} & \text{to P} & \text{to N} & \text{to R\&D} & \text{Sales} & \text{Costs}\\ \hline \text{P} & 87 & 170 & 19 & 819 & 426\\ \text{N} & 32 & 12 & 1 & 414 & 513\\ \text{R\&D} & 284 & 150 & 1 & 69 & 70\\ \hline \end{array} \]
The commercial vehicles division is currently incurring losses of 99 million GE. By how much would the total output of the company have to increase for the production of commercial vehicles to at least break even if, at the same time, costs in all divisions can be maintained at the current level by rationalization measures?
Note: You will need one of the following inverse matrices: \[ \small \begin{gathered} \left(\begin{array}{rrr} 0.9205 & -0.3704 & -0.0377\\ -0.0292 & 0.9739 & -0.0020\\ -0.2594 & -0.3268 & 0.9980\\ \end{array}\right)^{-1} =\left(\begin{array}{rrr} 1.11228 & 0.43740 & 0.04288\\ 0.03399 & 1.04090 & 0.00335\\ 0.30018 & 0.45451 & 1.01423\\ \end{array}\right)\\ \left(\begin{array}{rrr} 0.8840 & -0.3704 & -0.0377\\ -0.0292 & 1.0392 & -0.0020\\ -0.2594 & -0.3268 & 0.9385\\ \end{array}\right)^{-1} =\left(\begin{array}{rrr} 1.15928 & 0.42809 & 0.04747\\ 0.03323 & 0.97518 & 0.00340\\ 0.33195 & 0.45788 & 1.07984\\ \end{array}\right) \end{gathered} \]
Solution: New output vector \({\mathbf x}^\top =(1138.30, 562.05, 549.00)\), increase: \(191.35\)
-
A closed economy consists of two sectors. The following input-output table is provided (in million currency units, GE):
\[ \begin{array}{l|cc|c} & \text{Sector 1} & \text{Sector 2} & \text{Final consumption}\\ \hline \text{Sector 1} & 85 & 20 & 45\\ \text{Sector 2} & 70 & 58 & 62 \end{array} \]
If the deliveries of both sectors to the final consumption are to increase by 10%, to what value must the output of the sectors rise?
Solution: New output vector \({\mathbf x}^\top =(165, 209)\).