2 Mathematical Finance

The tasks we will solve throughout this chapter are among the simplest routine tasks in financial mathematics. They can be solved using formulas that can be looked up in collections of formulas, or by using tables or computers that are programmed for solving these tasks. Our goal is not to perfect the computational skills for solving these simplest financial mathematical tasks. Rather, we aim to understand the relationship between the economic concept of interest and its mathematical modeling so well that we are capable of creating the necessary formulas at any time and transforming them as needed.

2.1 Interest Models

We begin with the explanation of some basic concepts.

Let $K_0$ be a capital that is invested at an interest rate¹ $r$. This refers always to a specific time period, the compounding period. For the time being, we will assume that this is one year, but later we will allow any period lengths.

The interest rate is typically a number $r$ between $0$ and $1$, so $0\le r\le 1$. Under special economic conditions, interest rates can also be negative or greater than 1.

After one compounding period, interest in the amount of $K_0\cdot r$ accrues.

Remark 2.1 (Interpretation of Interest) Economics knows a number of economic interpretations of interest. A very well-known and prominent example is the Liquidity Preference Theory by John M. Keynes. Here, interest is interpreted as compensation for economic agents temporarily foregoing liquidity. In modern financial mathematics, interest is often considered as compensation for the risk creditors take when providing capital to debtors.

If at the end of one year, the interest $K_0r$ is added to the initial capital $K_0$, then $K_1$, the final capital at the end of the year is: \[ \begin{gathered} K_1=K_0+K_0r=K_0(1+r). \end{gathered} \] The factor $1+r$ is called the compounding factor. The equation \[ \begin{gathered} K_1=K_0(1+r) \end{gathered} \tag{2.1}\] is called the fundamental equation of financial mathematics and is the basis for all further considerations related to compounding.

We now imagine that interest is not only applied at the end of a single year but occurs over $t$ years. Let $K_1$ be the capital after the first year, $K_2$ the capital after the second year, etc. We want to calculate how high the capital $K_t$ will be after $t$ years.

There are two fundamentally different models of compounding. With simple interest, only the initial capital $K_0$ earns interest. With compound interest (interest on interest), the accrued interest also bears interest. Both models lead to different values for the final capital. Both models play a role in economic practice. Let’s now take a closer look at the mathematical description of both compounding models.

2.1.1 Simple Interest

The simple interest model is mathematically very easy to describe, as the capital develops according to the following linear scheme:

\[ \begin{gathered} \begin{array}{lclcl} K_1 &=& K_0+K_0r &=& K_0(1+r) \\ K_2 &=& K_1+K_0r &=& K_0(1+2r) \\ K_3 &=& K_2+K_0r &=& K_0(1+3r)\\ \ldots\\ K_t &=& K_{t-1}+K_0r &=& K_0(1+tr). \end{array} \end{gathered} \] From the last line of the scheme, we can read the relationship between the initial capital $K_0$, the final capital $K_t$, the interest rate $r$, and the term $t$: \[ \begin{gathered} K_t=K_0(1+tr). \end{gathered} \tag{2.2}\] The value $K_t$ is called the maturity value, $K_0$ the initial capital or present value of $K_t$. When we know three of the four values $K_0$, $K_t$, $t$, and $r$, we can calculate the fourth value. The key message of (2.2) is that with simple interest, the maturity value evolves as a linear function of the term $t$ with a rise equal to the yearly interest, namely $K_0r$.

Exercise 2.2 A capital of 2500 monetary units reaches the amount of 4450 monetary units after $12$ periods through simple interest. What is the interest rate?

Solution: To answer this question, we will insert the known values into the formula (2.2), which is \[ \begin{gathered} K_t = K_0(1 + tr) = 2500(1 + 12r) = 4450. \end{gathered} \] This equation is to be solved for $r$. Simple transformations yield \[ \begin{gathered} r = \frac{1}{t}\left(\frac{K_t}{K_0} - 1\right) = \frac{1}{12}\left(\frac{4450}{2500} - 1\right) = 0.065. \end{gathered} \] Therefore, the interest rate amounts to 6.5 percent. □

The model of simple interest is not limited to whole periods. It is also possible to calculate the capital development for parts of periods.

2.1.2 Compound Interest

Simple interest plays only a minor role in practice because of the linear and thus rather slow capital growth. The predominant interest model in economic practice is compound interest, i.e., interest on interest. With this interest model, the capital amount develops according to the following scheme: \[ \begin{gathered} \begin{array}{lclclcl} K_1 &=& K_0 + K_0r &=& K_0(1 + r) \\ K_2 &=& K_1 + K_1r &=& K_1(1 + r) &=& K_0(1 + r)^2 \\ K_3 &=& K_2 + K_2r &=& K_2(1 + r) &=& K_0(1 + r)^3\\ \ldots \\ K_t &=& K_{t-1} + K_{t-1}r &=& K_{t-1}(1 + r) &=& K_0(1 + r)^t. \end{array} \end{gathered} \] From the last equation, we can again read off the relationship between the initial capital $K_0$, the final value $K_t$, the interest rate $r$, and the term $t$: \[ \begin{gathered} K_t = K_0(1 + r)^t. \end{gathered} \tag{2.3}\] This equation is called the future value equation of compound interest. The quantity $1 + r$ is so important that we have a separate term and symbol for it: \[ \begin{gathered} Accrual factor:\quad q = 1 + r. \end{gathered} \] We see that in the mathematical description of this interest model, the future value equation, powers occur. The future value $K_t$ of the capital is created by multiplying the initial capital $K_0$ with the $t$-th power of the accrual factor $q^t = (1 + r)^t$. It is also said that the future value $K_t$ is obtained by compounding the initial capital over $t$ years.

This interest model can also be used for any arbitrary interest duration $t$.

The future value equation (2.3) establishes the relationship between the variables $K_0$, $K_t$, $t$, and $r$ when dealing with compound interest. If three of these variables are known, then the fourth one is uniquely determined and can be calculated. In this case, the basic equation is somewhat more complicated than with simple interest. We will therefore take a closer look at how we can calculate each of the four involved variables.

Calculation of the Future Value

The future value equation itself indicates how the future value $K_t$ of the capital is to be calculated.

Exercise 2.3 What is the future value of the capital $K_0 = 1000$ after 10 years at an interest rate of $r = 0.075$?

Solution: The future value amounts to: \[ \begin{gathered} K_{10} = K_0(1 + r)^{10} = 1000(1 + 0.075)^{10} = 2061.03. \end{gathered} \] □

Calculation of the Present Value

To calculate the initial capital $K_0$, the present value of $K_t$, we start again from the future value equation (2.3) and by transforming it we get \[ \begin{gathered} K_0 = \frac{K_t}{(1 + r)^t} = K_t\left(\frac{1}{1 + r}\right)^t. \end{gathered} \tag{2.4}\] The quantity $1 / (1 + r)$ is also so significant that we have a separate term for it, discount factor or capitalization factor, and a separate symbol, namely $d$: \[ \begin{gathered} Discount factor:\quad d = \frac{1}{1 + r}. \end{gathered} \]

The present value $K_0$ of the capital $K_t$ is thus created by multiplying the future value $K_t$ with the $t$-th power $d^t$ of the discount factor: $K_0 = K_td^t$. In brief: the future value is discounted over $t$ years.

Exercise 2.4 What is the present value of a capital $K_{10} = 30000$ at an interest rate of $r = 0.05$?

Solution: The discount factor is \[ \begin{gathered} d = \frac{1}{1 + r} = \frac{1}{1.05}, \end{gathered} \] and therefore, the present value is: \[ \begin{gathered} K_0 = K_{10}d^{10} = \frac{30000}{1.05^{10}} = 18417.40. \end{gathered} \] □

Exercise 2.5 A person A is obligated to make a payment of 10000 monetary units to a person B in 5 years. After one year, it is agreed to make an equivalent payment immediately. How much should this payment be if an interest rate of 8% is assumed?

Solution: If A is willing to make the payment prematurely, the amount that needs to be paid is the present value of the debt $K_5=10000$. The discount factor is $d=\frac{1}{1+r}=1/1.08$, and after the first year, there remains a term of 4 years.

This results in a present value after one year \[ \begin{gathered} K_1=K_5d^4=\frac{10000}{1.08^4}=7350.30\,. \end{gathered} \] □

The last example clearly shows why the present value is also called present value of a debt: it is today’s value of a debt that is due in the future.

Calculation of the interest rate

Our next task is to calculate the interest rate $r$ from the other quantities.

With simple transformations from the future value equation (2.3), we obtain \[ \begin{gathered} \begin{array}{lcl} K_t=K_0(1+r)^t &\Rightarrow& \displaystyle\frac{K_t}{K_0}=(1+r)^t \\ &&\\ &\Rightarrow& \displaystyle 1+r=\sqrt[t]{\frac{K_t}{K_0}} =\Big(\frac{K_t}{K_0}\Big)^{1/t} \\ &&\\ &\Rightarrow& \displaystyle r=\Big(\frac{K_t}{K_0}\Big)^{1/t}-1. \end{array} \end{gathered} \] We see that the solution involves taking a $t$-th root. However, roots can also be considered as powers with fractional rational exponents.

Exercise 2.6 What interest rate is required for a capital to double within 10 years?

Solution: If the capital is supposed to double within 10 years, that means $K_{10}=2K_0$. Accordingly, we have \[ \begin{gathered} K_{10}=K_0(1+r)^{10}=2K_0,\;\text{therefore}\; (1+r)^{10}=2. \end{gathered} \] By solving this equation for $r$, we obtain the interest rate by \[ \begin{gathered} r= 2^{1/10}-1=0.071773\simeq 7.18 \;\text{percent}. \end{gathered} \] □

For the following example, we need a new term from financial mathematics:

Definition 2.7 (Zero Bond) A Zero Bond or Zero-coupon bond is a debt security that does not pay interest or amortization during the term. The interest, including compound interest, is paid only at the end of the term along with the redemption (face value).

Exercise 2.8 Someone buys a zero bond at an issue price of 80,245.10 CU, with a term of five years, and a promised redemption value (face value) of 100,000 CU. What is the yield of this security?

Solution: In this context, yield is nothing else than the interest rate $r$ that is achieved with this debt security. The debt equals the issue price (present value), and the promised redemption is the future value of the debt.

The future value equation applies (2.3), which we solve for $r$: \[ \begin{gathered} 100000 = 80245.10 \cdot (1+r)^5\implies r=\sqrt[5]{\frac{100000}{80245.10}}-1 =0.045\,. \end{gathered} \] Thus, a yield of 4.5% is achieved. □

Exercise 2.9 A company plans to erect a new production facility in 15 years. It is estimated that the construction costs will be 30 million CU in 15 years. Therefore, funds are being invested at a bank at an interest rate $r$, which with interest and compound interest is supposed to grow to 30 million CU in 15 years, the amount necessary to finance the plant. However, after 6 years, the bank lowers the interest rate to 6%. To achieve the planned goal, the company must add an amount of 1,438,942 CU. What was the invested capital, the original interest rate?

Solution: Let $K_0$ denote the initial sum invested and $r$ the initial interest rate. If everything had gone according to plan, meaning the interest rate was not reduced, then it would be: \[ \begin{gathered} K_0(1+r)^{15}=30\,000\,000. \end{gathered} \] However, after 6 years the interest rate drops to 6%, and the subsequent development follows the equation: \[ \begin{gathered} \left[K_0(1+r)^6 + 1\,438\,942\right] \cdot 1.06^9=30\,000\,000. \end{gathered} \] We must solve this system of equations in the variables $K_0$ and $r$. To do this, we calculate $K_0$ from the first equation: \[ \begin{gathered} K_0=\frac{30\,000\,000}{(1+r)^{15}}, \end{gathered} \] and substitute that into the second equation: \[ \begin{gathered} \left[\frac{30\,000\,000}{(1+r)^{15}}\,(1+r)^6 + 1\,438\,942\right] \cdot 1.06^9 = 30\,000\,000. \end{gathered} \] We simplify: \[ \begin{gathered} \frac{30\,000\,000}{(1+r)^9}=\frac{30\,000\,000}{1.06^9}-1\,438\,942 =16\,318\,011.91\\[5pt] \frac{1}{(1+r)^9}=\frac{16\,318\,011.91}{30\,000\,000}=0.543934\\[5pt] (1+r)^9=1.838459\\[5pt] 1+r = 1.838459^{1/9}=1.07\,. \end{gathered} \] Therefore, the original interest rate was $r=0.07$. The initial capital invested was: \[ \begin{gathered} K_0=\frac{30\,000\,000}{1.07^{15}}=10\,873\,380.59\,. \end{gathered} \] □

2.2 Maturities

2.2.1 Exponential Equations

We have not yet dealt with the task of calculating the maturity $t$, i.e., the number of periods from the other sizes $K_0,\,K_t,\,r$ in the context of compound interest.

However, if we want to calculate the maturity $t$, then we must extract the unknown $t$ from the exponent in our basic equation $K_t=K_0(1+r)^t$. Such an equation is therefore called an exponential equation.

With the tools of power arithmetic, we can only solve equations of the form $x^p=b$. Such an equation, where the unknown $x$ is in the base, is called a power equation. Then, as we know, $x=b^{1/p}$, provided $p\not=0$ and $b>0$.

A general exponential equation has the form $a^x=b$. With the tools of power arithmetic, it is not possible to give a closed formula for $x$ that would be evaluable with a calculator or computer. For this, we need a new mathematical concept, namely the logarithm.

The Logarithm

As is known, $10^p$ is a positive number for all exponents $p\in\mathbb R$. Now we are concerned with the reverse problem: Is there any exponent $p$ for every positive number $b>0$ with the property $10^p=b$? It can be generally proven that this question can be answered positively:

Definition 2.10 Let $b>0$ be a positive number. Then the exponent $p\in\mathbb R$ with the property $10^p=b$ is called the logarithm of $b$ to the base $10$. The notation used is $p=\log b$.

The fundamental relationship holds: \[ \begin{gathered} b=10^{\log b}. \end{gathered} \tag{2.5}\]

We illuminate this definition with some examples:

Since $1=10^0$, $\log 1=0$. Moreover: \[ \begin{aligned} %% {alignat*}{3} 10&=10^1&\quad\implies &\log 10&=1\\ 100&=10^2&\quad\implies &\log 100&=2&,\quad etc.\\ 0.1 &=10^{-1}&\quad\implies &\log 0.1&=-1\\ 0.01 &=10^{-2}&\quad\implies &\log 0.01&=-2&,\quad etc. \end{aligned} \] For numbers that are not whole number 10 powers, we need a calculator. With its help we find, for example: \[ \begin{gathered} \log 11=1.041393,\quad\log 0.75=-0.124939\,. \end{gathered} \]

Remark 2.11 To define the logarithm, some additional explanations are needed. First, it appears arbitrary to use the base 10 as the foundation for the definition of the logarithm. Such an objection is certainly justified. In principle, a logarithm can be defined using any positive number $a$ as a base. However, to solve arbitrary exponential equations, a single such definition suffices. And for reasons of cultural tradition, it is customary to use the base 10 (decimal logarithms). Things don’t remain quite so simple, though. We will later turn to a different base to define a logarithm. But this is for different reasons than solving exponential equations.

How does one calculate the logarithm of a number? In reality, it is not very easy to find the logarithm $p$ of a number $b>0$. This is why logarithms were tabulated in the 17th century for practical applications. Today we use computers for numerical calculation of logarithms.

The logarithm has several characteristic features which we can formulate as calculation laws.

Theorem 2.12 (Arithmetic Laws)

The logarithm with base 10 is equal to 1, i.e. $\log 10 = 1$.
The logarithm of a product is equal to the sum of the logarithms of the factors, i.e. for $a,b>0$: \[ \begin{gathered} \log(a\cdot b)=\log a+\log b \end{gathered} \tag{2.6}\]
The logarithm of a quotient is equal to the difference of the logarithms of the numerator and the denominator, i.e. for $a,b>0$: \[ \begin{gathered} \log\left(\frac{a}{b}\right)=\log a-\log b \end{gathered} \tag{2.7}\]
For the logarithm of a power, we have: \[ \begin{gathered} \log a^b = b\log a \end{gathered} \tag{2.8}\]

The power rule (2.8) is precisely the tool we need to solve the exponential equation $a^x=b$.

Solving Exponential Equations

Now it’s finally time. We want to see how logarithms can be applied. Our currently most important application of logarithms is to solve exponential equations.

An exponential equation has the form $a^x=b$ with $a,b>0$ and $a\ne 1$. Let’s look at how exponential equations are generally solved.

The equation is logarithmized, i.e., we take the logarithm of both sides. After applying the rule (2.8), we can then calculate $x$: \[ \begin{gathered} \begin{array}{lcl} a^x=b &\Rightarrow& \log a^x=\log b \\ &&\\ &\Rightarrow& x\log a=\log b \\ &&\\ &\Rightarrow& x=\dfrac{\log b}{\log a}. \end{array} \end{gathered} \]

Example 2.13

We want to solve the equation $3^x=7$. This is an exponential equation because the unknown $x$ is in the exponent. We take the logarithm of both sides of the equation: \[ \begin{gathered} \log 3^x=\log 7. \end{gathered} \] Now the arithmetic law (2.8) is applied. It tells us that $\log 3^x=x\log 3$. Thus, our equation takes the form \[ \begin{gathered} x\log 3=\log 7. \end{gathered} \] By dividing by $\log 3$, we obtain the solution \[ \begin{gathered} x=\frac{\log 7}{\log 3}=\frac{0.845098}{0.477121}=1.771244. \end{gathered} \] Here we have rounded the results to 6 places. A check calculation shows us: \[ \begin{gathered} 3^{1.771244}=7.000001929\simeq 7. \end{gathered} \] As a second numerical example, we solve the exponential equation $0.99^x=0.5$. We take logarithms on both sides again and obtain \[ \begin{gathered} x=\frac{\log 0.5}{\log 0.99}= \frac{-0.301030}{-0.004365}=68.967564. \end{gathered} \]

2.2.2 The Calculation of Maturities

The logarithm and solving exponential equations are important tools in dealing with financial mathematics tasks. This section is about calculating maturities of capital investments.

Exercise 2.14 How long must 1000 monetary units (MU) be invested at 5% with compound interest for the end capital to be 1500 MU?

Solution: If we insert the figures into the basic equation $K_t=K_0(1+r)^t$, we arrive at the exponential equation \[ \begin{gathered} 1500=1000\cdot 1.05^t. \end{gathered} \] The unknown maturity $t$ is to be calculated. We simplify and logarithmize: \[ \begin{gathered} 1.5=1.05^t\quad\Rightarrow\quad \log 1.5 =t\log 1.05 \quad \Rightarrow\quad t=\dfrac{\log 1.5}{\log 1.05}=8.31\,. \end{gathered} \] The required maturity is therefore 8.31 years. □

Let’s look at one more example.

Exercise 2.15 How long does it take for the capital in a savings account with an 8 percent interest rate to double through compounding?

Solution: This is a typical task that leads to an exponential equation and can be solved using logarithms.

Let $K_0$ be an initial capital. We are looking for that maturity $t$ for which \[ \begin{gathered} K_0\cdot 1.08^t=2K_0 \implies 1.08^t=2. \end{gathered} \] If we solve this exponential equation, we get the result \[ \begin{gathered} t=\frac{\log 2}{\log 1.08}=9.0065\simeq 9\text{ years}. \end{gathered} \] □

Let’s consider the issue of the last example a bit more generally.

Let $K_0$ be an initial capital and $r$ a rate of interest. After how much time $t$ does the capital reach the amount of $aK_0$, where $a>1$ denotes the multiplication factor?

This question leads to the equation \[ \begin{gathered} K_0(1+r)^t=aK_0 \text{ or } (1+r)^t=a, \end{gathered} \] where $t$ is to be calculated. This is an exponential equation. We logarithmize both sides and derive \[ \begin{gathered} t=\frac{\log a }{\log (1+r) }. \end{gathered} \]

Exercise 2.16 For how long must $8663$ MU be invested at $4$% compound interest for the final capital, further invested at $4$%, to yield $600$ MU in interest per year?

Solution: The final capital $K_t$ is obtained from the initial capital by \[ \begin{gathered} K_{t}=K_{0}\cdot (1+r)^t=8663\cdot(1+0.04)^t=8663\cdot1.04^t. \end{gathered} \] For this final capital, the annual interest earned is \[ \begin{gathered} K_{t}\cdot r=8663\cdot1.04^t\cdot0.04=600. \end{gathered} \] From this exponential equation, we can calculate the term: \[ \begin{gathered} 1.04^t=\frac{600}{0.04\cdot8663} \quad\Rightarrow\quad t=13.9974\,. \end{gathered} \] Therefore, the initial capital must be invested for approximately $14$ years. □

We conclude the section with a somewhat more complex example.

Exercise 2.17 A zero-coupon bond with a face value of 500,000 CU is purchased for a price of 372,047 CU. The bond has an annual interest rate of 3%. What is its term?

Solution: From the formula for the final value, we get the exponential equation: \[ \begin{gathered} 500000=372047\cdot 1.03^t\,. \end{gathered} \] We find its solution by taking logarithms: \[ \begin{gathered} t=\frac{\log(500000/372047)}{\log 1.03}=10 \quad\text{years}. \end{gathered} \] □

2.3 Geometric Sequences

2.3.1 Sequences

The terms of an arithmetic sequence have constant differences. Another way to express changes between consecutive terms is by forming relative differences: \[ \begin{gathered} \frac{\Delta x_n}{x_{n-1}}=\frac{x_n-x_{n-1}}{x_{n-1}}=\frac{x_n}{x_{n-1}}-1. \end{gathered} \] The relative difference indicates the gap between $x_n$ and $x_{n-1}$ as a fraction (or percentage) of $x_{n-1}$.

Example 2.18

Let $x_n$ be a sequence containing the share prices of a stock at consecutive times. For example, let \[ \begin{gathered} x_0=100,\; x_1=120,\; x_2=125,\;x_3=115, \;x_4=120,\;x_5=130. \end{gathered} \] In the economic interpretation, the differences in share prices are less interesting. What’s essential is the relative change in value, which in economic applications is termed yield or return. The relative value change or yield of our stock in the first period is \[ \begin{gathered} \frac{\Delta x_1}{x_0}=\frac{120-100}{100}=0.2=20\,\%, \end{gathered} \] in the second period \[ \begin{gathered} \frac{\Delta x_2}{x_1}=\frac{125-120}{120}=0.0417=4.17\,\%, \end{gathered} \] in the third period \[ \begin{gathered} \frac{\Delta x_3}{x_2}=\frac{115-125}{125}=-0.08=-8\,\%, \end{gathered} \] and so on. It is the relative changes (percentage changes) or yields that economically contain the essential information about the change in value.

Since relative differences (yields) are much more important for applications in the field of economics than absolute differences, sequences with constant relative differences also play a much more important role in economic applications than arithmetic sequences.

Definition 2.19 A number sequence $x_n$ is a geometric sequence if the relative differences between subsequent terms are constant.

Let $x_n$ be a geometric sequence with a constant relative difference \[ \begin{gathered} r=\frac{x_n-x_{n-1}}{x_{n-1}}=\frac{x_n}{x_{n-1}}-1. \end{gathered} \] Clearly, the quotient of consecutive terms \[ \begin{gathered} \frac{x_n}{x_{n-1}}=1+r=:q \end{gathered} \] is also constant. Therefore, we could have just as well defined geometric sequences by the property that the quotient of consecutive terms is constant.

Example 2.20 (Geometric Sequences)

The sequence with the general term $x_n=1.1^n$ is a geometric sequence, because the quotient $x_n/x_{n-1}=1.1^n/1.1^{n-1}=1.1$ is constant. Therefore, $q=1.1$ and the relative difference between two consecutive terms is $r=q-1=0.1$ or $10\,\%$.

The sequence with the general term $x_n=2^n$ is a geometric sequence because the quotient $x_n/x_{n-1}=2^n/2^{n-1}=2$ is constant. Thus $q=2$ and the relative difference between two consecutive terms is $r=q-1=1$ or $100\,\%$. The sequence terms double their value at each step.

Let $x_n=x_0+nd$ be an arithmetic sequence with a difference $d\not=0$. This is not a geometric sequence, because the relative difference between two consecutive terms is \[ \begin{gathered} \frac{\Delta x_n}{x_{n-1}}=\frac{d}{x_0+(n-1)d}, \end{gathered} \] and this is not constant; rather it changes with $n$. In fact, it becomes smaller as $n$ grows.

The sequence with the general term $x_n=n^2$ is also not a geometric sequence, as the quotient $x_{n+1}/x_n=(n+1)^2/n^2=(1+1/n)^2$ is not constant but depends on $n$.

Geometric sequences often occur in economic applications. Most forms of savings, repayment of loans, but also provision for pensions are based on geometric sequences.

Example 2.21

Let $K_0$ be a capital that is invested at an interest rate $r$. The sequence of capital amounts $K_n=K_0(1+r)^n$ is then a geometric sequence with the ratio $q=1+r$. The ratio $q=1+r$ is also the capitalization factor. The interest rate $r$ is the relative increase of the capital: \[ \begin{gathered} K_{n+1}=K_n(1+r) \;\Rightarrow\; r=\frac{K_{n+1}-K_n}{K_n}. \end{gathered} \]

Subsequent Terms

It is also possible to recognize geometric sequences by the term of their general element.²

Theorem 2.22 A sequence with the general element $x_n$ is a geometric sequence if and only if the general element has the form \[ \begin{gathered} x_n=x_0q^n=x_0(1+r)^n \end{gathered} \tag{2.9}\]

Proof: Let $x_n$ be an arbitrary geometric sequence with the initial value $x_0$ and the ratio $q$. Then we obtain the elements of the sequence consecutively by \[ \begin{gathered} \begin{array}{lclcl} x_1&=&&&x_0q\\ x_2&=&x_1q&=&x_0q^2\\ x_3&=&x_2q&=&x_0q^3\\ &&\ldots&&\\ x_n&=&&=&x_0q^n. \end{array} \end{gathered} \] Therefore, the general term of the sequence has the form $x_n=x_0q^n$.

Conversely, let $x_n$ be any sequence with the term $x_n=Aq^n$. Then $x_n/x_{n-1}=q$, which is constant. It’s clear that $x_0=A$ is the initial value of the sequence and $q$ is the constant ratio of two successive elements. □

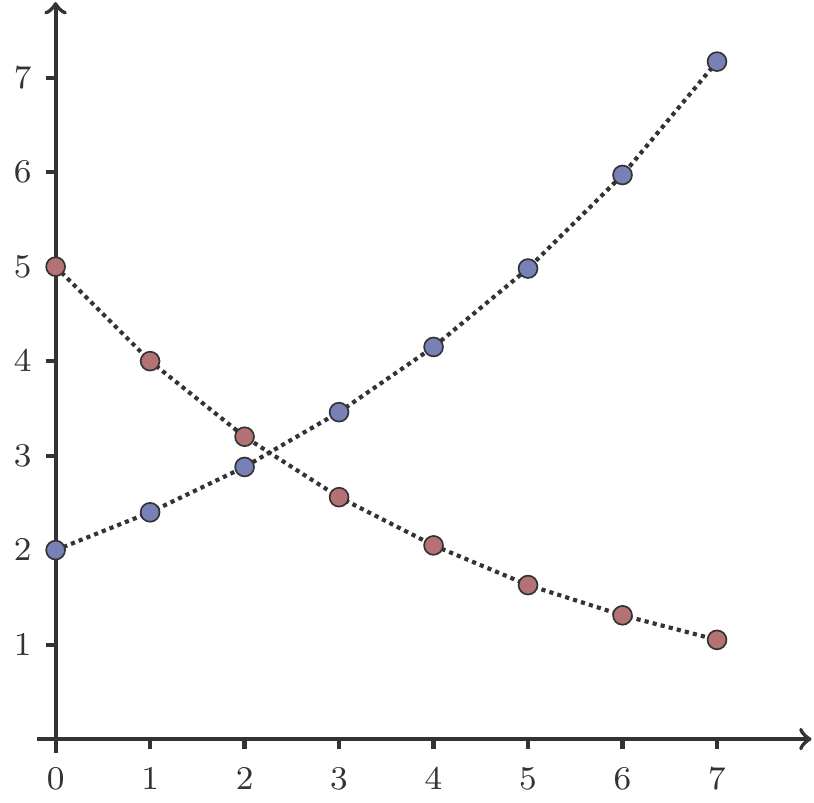
Example 2.23 (Properties of Geometric Sequences)

Let $x_n=2\cdot1.2^n$ be the geometric sequence with the initial value $x_0=2$ and the ratio $q=1.2$. The relative difference between two consecutive elements is $r=q-1=0.2$, which means that each element is $20\%$ larger than its predecessor. Therefore, the sequence is strictly monotonic increasing: Each element of the sequence is larger than its predecessor.

Let $x_n=5\cdot 0.8^n$ be the geometric sequence with the initial value $x_0=5$ and the ratio $q=0.8$. The relative difference between two consecutive elements is $r=q-1=-0.2$, which means that each element is $20\%$ smaller than its predecessor. Therefore, the sequence is strictly monotonic decreasing: Each element of the sequence is smaller than its predecessor. See Figure 2.1.

Figure 2.1: The sequences $x_n=5\cdot 0.8^n$ and $x_n=2\cdot 1.2^n$.

2.3.2 Summation of Sequences

Sum Formula

We now provide a formula that allows us to directly calculate the sum of a geometric sequence.

Theorem 2.24 (Geometric Sum Formula) The sum of the first $n$ terms of a geometric sequence is, if $q\not=1$, \[ S_n= x_0+x_0q+x_0q^2+\cdots+x_0q^{n-1}=x_0\cdot\dfrac{q^n-1}{q-1}. \tag{2.10}\]

Justification: If we subtract the equations \[ \begin{gathered} \begin{array}{lclclclclcl} S_n &=& x_0 &+& x_0q &+& x_0q^2& + & \ldots & + & x_0q^{n-1}\\ qS_n &=& x_0q &+& x_0q^2 &+& x_0q^3& + & \ldots & + & x_0q^{n}\\ \end{array}, \end{gathered} \] then we obtain \[ \begin{gathered} S_n-qS_n=x_0-x_0q^n\implies S_n(1-q)=x_0(1-q^n), \end{gathered} \] from which the formula for the partial sums follows. □

Example 2.25

The geometric sequence $x_n=(\frac{1}{2})^{n}$ has the initial value $x_0=1$ and the ratio $q=\frac{1}{2}$. This implies for the partial sums \[ \begin{gathered} S_n=\frac{ 1-(\frac{1}{2})^n}{1-\frac{1}{2}} =2-\Big(\frac{1}{2}\Big)^{n-1}. \end{gathered} \]

Applications

We will explore financial applications of geometric sums in the next section. Therefore, we will focus on other examples here.

Our first application example is based on a famous legend.

Example 2.26

The inventor of chess, Sissa ibn Dahir, asked the Indian king Shihram for a reward of a quantity of wheat grains that one would receive if one wheat grain is placed on the first square of the chessboard and on each subsequent square twice the number of wheat grains are placed. How many wheat grains does this amount to?

Let $x_n$ be the number of wheat grains that are placed on the $n$-th square of the chessboard. The sequence $x_n$ is a geometric sequence with the first term $x_0=1$ and because of the required doubling with the ratio $q=2$. Therefore, the sum of the 64 sequence terms is \[ \begin{gathered} S_{64}= x_0\frac{q^{64}-1}{q-1}=2^{64}-1. \end{gathered} \] When you calculate this number exactly, you get \[ \begin{gathered} S_{64}=18\; 446\; 744\; 073\; 709\; 551\; 615 \;\approx\; 18,447\cdot 10^{15}. \end{gathered} \] To comprehend the amount of wheat grains, we will calculate their volume.

A cubic meter contains approximately 16 million wheat grains, which is $1.6\cdot 10^{7}$ wheat grains. Therefore, our quantity of wheat grains has a volume of \[ \begin{gathered} V=\frac{18,447\cdot 10^{15}}{1.6\cdot 10^{7}}\approx11,529\cdot 10^{8}\, \approx 1.2\cdot 10^{12}\,m^3. \end{gathered} \] A cubic kilometer contains $1000^3=10^9$ cubic meters. Hence, $V=1.2\cdot 10^{3}=1,200$ cubic kilometers. This corresponds to a cube with an edge length of more than 10 kilometers.

Exercise 2.27 The population of a city grows in the first year from 15,000 to 15,600. This corresponds to a growth rate of $600/15,000=0.04=4\%$. Every resident produces $1\,m^3$ of waste per year. This waste is taken to a landfill, which currently has space for 1 million $m^3$. How do the annually generated and the total accumulated waste volumes develop? How long will the landfill space last?

Solution: To calculate the amount of garbage accumulated over the course of a year, we need the average population number of a year. For simplicity, let us assume that the average population in the first year is $15,300=\frac{1}{2}(15000+15600)$[^1]. Thus, the amount of garbage produced in the first year amounts to $15,300 \;m^3$. Since the population grows by 4 percent each year, the same applies to the amount of garbage generated. It forms a geometric sequence with the ratio $q=1.04$. Therefore, the total amount of garbage after $n$ years is \[ \begin{gathered} S_n=15,300\,\frac{1.04^n-1}{1.04-1}. \end{gathered} \] The landfill must be closed when $S_n=1,000,000.$ Therefore, the equation \[ \begin{gathered} 1,000,000=15,300\,\frac{1.04^n-1}{1.04-1} \end{gathered} \] must be solved for $n$. This leads to the exponential equation \[ \begin{gathered} 1.04^n=1+0.04\,\frac{1,000,000}{15,300}, \end{gathered} \] which we can solve using logarithms. The solution yields $n=32.7613$. The landfill must be closed after approximately 33 years. □

2.4 Financial Mathematics of Annuities

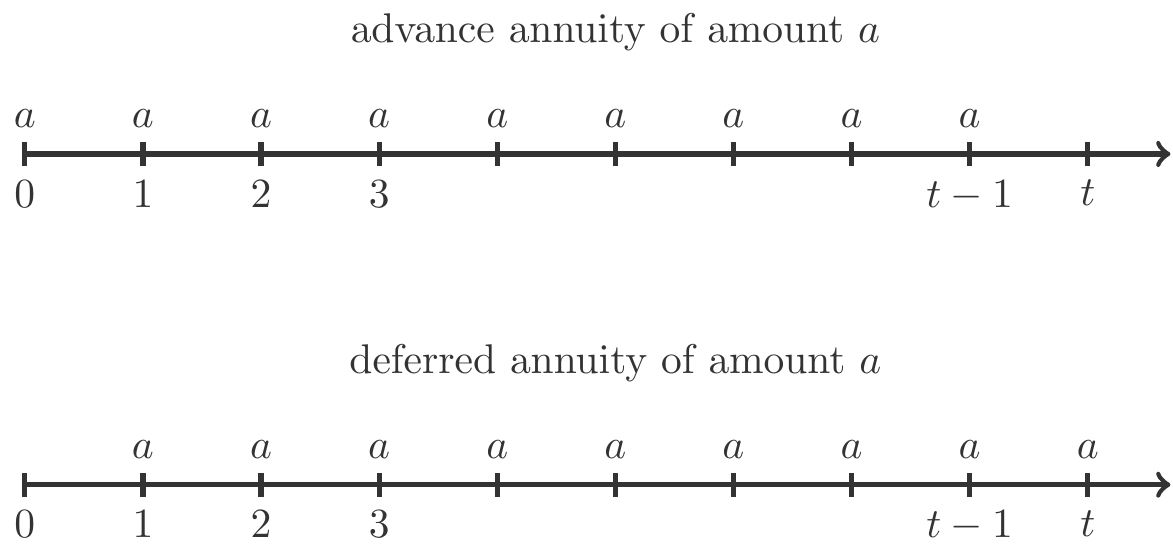
In financial mathematics, geometric series, which we call sums over geometric sequences, are especially common in the context of annuities. An annuity is a periodic series of payments that are typically equal in amount. If the payments are made at the beginning of each period, it is called an advance annuity. If they are always made at the end of a period, then the annuity is deferred. Figure 2.2 schematically shows the difference between advance and deferred annuity payments of the amount $a$.

Figure 2.2: Temporal allocation of annuity payments.

A financial annuity corresponds to a cash flow, and our next task will be to evaluate such cash flows taking into account the interest rates. The following questions will have to be answered:

What capital is accumulated over time (capital formation)?
What capital is required to make the payments over a certain period of time (annuitization)?

This evaluation problem is more challenging to solve than the valuation tasks we have dealt with in this chapter so far, because the payments $a$ occur at different times.

In financial mathematics, the solution to the valuation problem is based on a simple principle.

Equivalence Principle of Financial Mathematics

To compare payments that occur at different times, they are related back to the same point in time $T$.

The choice of $T$ is irrelevant.

A look at Figure 2.2 shows that two points in time are particularly interesting:

$T=0$: The payments $a$ are in the future, the valuation takes place before the due date of the payments. Their present value, i.e., their discounted value, is therefore obtained by discounting.
$T=t$: The payments $a$ occur before $T$, the valuation takes place after their maturity, their future value is thus obtained by compounding.

Present value of an annuity due

We first address the case of $T=0$, with the payments $a$ being made in advance.

The first payment $a$ takes place at time $0$ and therefore has the present value $a$. The second payment occurs at time $1$ and its present value is $ad$, see Figure 2.3. The last payment takes place at time $t-1$, its present value is $ad^{t-1}$.

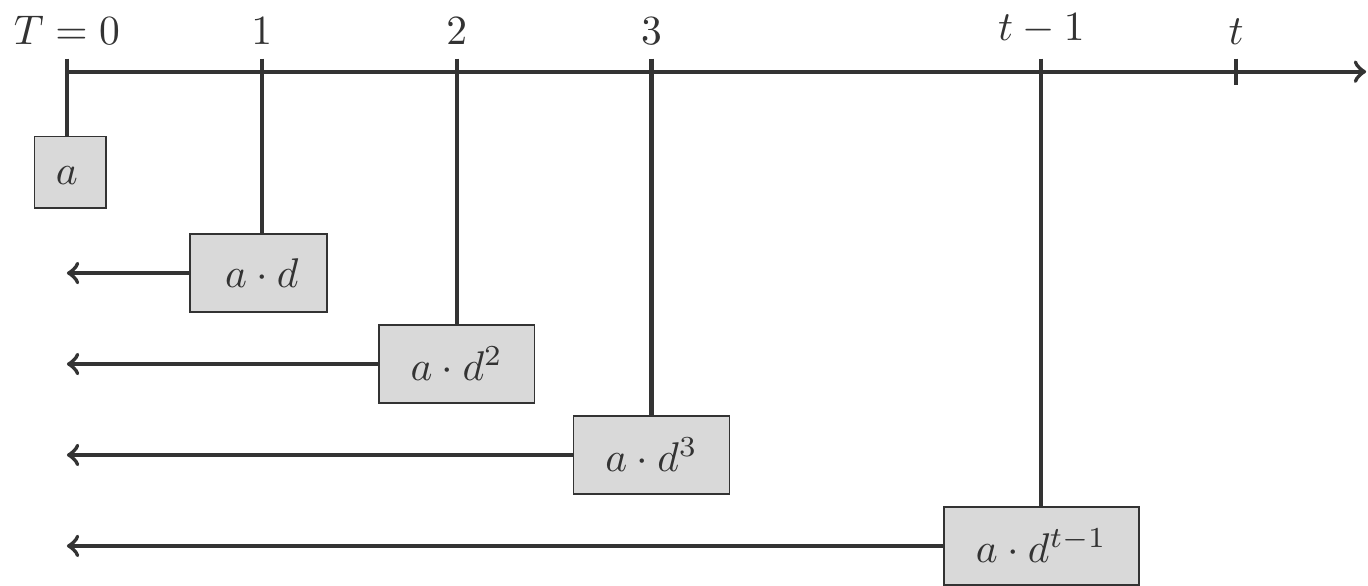
Figure 2.3: The present value of an annuity due.

The present values of all $t$ payments are therefore \[ \begin{gathered} a,\;ad,\;ad^2,\;ad^3,\ldots,\;ad^{t-1}, \end{gathered} \] and they form a geometric sequence. The sum of these present values is called the present value of an annuity due \[ \begin{gathered} \begin{array}{lcl} B_t& =&a+ad+ad^2+ad^3+\cdots+ad^{t-1}\\[5pt] &=& a(1+d+d^2+d^3+\cdots+d^{t-1})\\[5pt] &=& a\,\dfrac{1-d^t}{1-d}. \end{array} \end{gathered} \tag{2.11}\] The present value of an annuity due is therefore, apart from the factor $a$ which indicates the amount of the annuity, simply the partial sum of a geometric series with the quotient $d$, which we calculate using Theorem 2.24.

Present value of a regular annuity

The present value of a regular annuity is calculated in a very similar way. The only difference is that the payments occur one period later. For determining their present value, these therefore have to be discounted one more period. Thus, the present value of a regular annuity is: \[ \begin{gathered} \begin{array}{lcl} B_t& =&ad+ad^2+ad^3+ad^4+\cdots+ad^{t}\\[5pt] &=& ad(1+d+d^2+d^3+\cdots+d^{t-1})\\[5pt] &=& ad\,\dfrac{1-d^t}{1-d}. \end{array} \end{gathered} \tag{2.12}\]

Future value of an annuity due

Now we examine the valuation at $T=t$, and we start again with the case where the payments are made in advance.

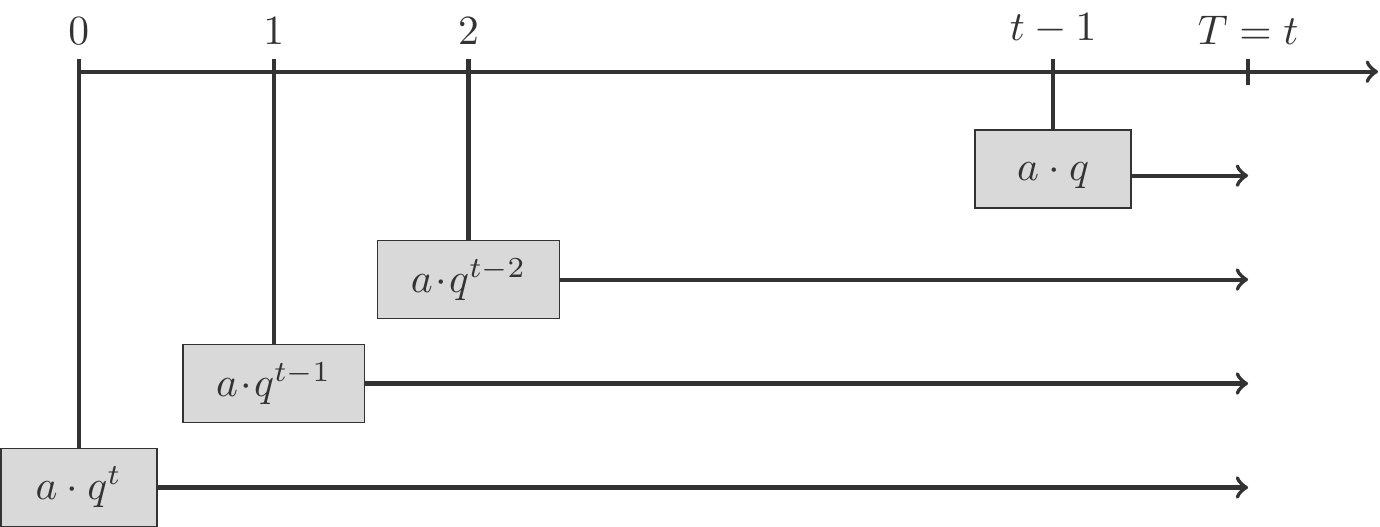
The first payment $a$ is made at time $0$ and therefore has the final value $aq^t$. The second payment is made at time $1$ and its final value is $aq^{t-1}$. The last payment is made at time $t-1$. This needs to be invested for one more period because the legal transaction, on which the payment obligation or claim is based, does not end until time $t$. Therefore, its final value is $aq$, see Figure 2.4. The final values of all $t$ payments are \[ \begin{gathered} aq^t,\;aq^{t-1},\;aq^{t-2},\;aq^{t-3},\ldots,\;aq. \end{gathered} \] The sum of these final values of individual payments is the final value of the annuity \[ \begin{gathered} \begin{array}{lcl} E_t& =&aq^t+aq^{t-1}+aq^{t-2}+aq^{t-3}+\cdots+aq\\[5pt] &=& aq(q^{t-1}+q^{t-2}+q^{t-3}+\cdots+1)\\[5pt] &=& aq\,\dfrac{q^t-1}{q-1}. \end{array} \end{gathered} \tag{2.13}\] The final value of an annuity in advance is therefore the partial sum of a geometric series multiplied by the factor $aq$ with the quotient $q$.

Only little changes when the payments are made in arrears: each payment is compounded one period less often. The final value of an annuity in arrears is therefore: \[ \begin{gathered} \begin{array}{lcl} E_t& =&aq^{t-1}+aq^{t-2}+aq^{t-3}+aq^{t-4}+\cdots+a\\[5pt] &=& a(q^{t-1}+q^{t-2}+q^{t-3}+\cdots+1)\\[5pt] &=& a\,\dfrac{q^t-1}{q-1}. \end{array} \end{gathered} \tag{2.14}\]

Relationship between Present Value and Final Value

However, there is also another method to determine these final values. The present value and the final value are valuations of the same performance at different points in time. This equivalence must necessarily result in the final value of the annuity being identical to the final value of $B_t$, i.e. \[ \begin{gathered} E_t=B_tq^t. \end{gathered} \tag{2.15}\] In (2.15) $B_t$ and $E_t$ are both either in advance or in arrears.

We obtained this equation based on our understanding of the significance of the underlying concepts. The validity of the equation (2.15) is not immediately apparent in our formulas (2.11) and (2.13) for the annuity in advance. However, we can convince ourselves of this by calculation. We use the fact that $d=1/q$. We thus see that in the case of an annuity in advance \[ \begin{gathered} B_tq^t=a\,\frac{1-d^t}{1-d}q^t= a\,\frac{(1-1/q^t)q^t}{1-1/q}=a\,\frac{q^t-1}{1-1/q}=aq\,\frac{q^t-1}{q-1}=E_t. \end{gathered} \] So both methods lead to the same final value of an annuity in advance. Of course, a similar argument can be made for the relationship between the present value and final value of an annuity in arrears.

2.4.1 Applications

Exercise 2.28 An insurance company offers home insurance for single-family homes. For an insurance value (coverage amount) of 300,000 GE, the annual premium, which is always due at the end of the year, is 10,100 GE. How many years does it take until the promised compensation payment of 300,000 GE for a certain policyholder is covered by the received premium payments and their interest (interest rate 4%)?

Solution: The premium payments of the insured represent a financial annuity with payment $a=10100$. This annuity is post-due because the payments are made at the end of the year; the interest rate is $r=0.04$.

We are interested in how long it takes until the received premium payments including compound interest reach the promised coverage amount of 300,000. Therefore, we interpret this coverage amount as the final value of the annuity!

We use formula (2.14) and first solve for $q^t$: \[ \begin{gathered} E=a\,\frac{q^t-1}{q-1}\implies q^t=\frac{E(q-1)}{a}+1\,. \end{gathered} \] Now we insert the numerical information and solve the exponential equation by taking logarithms: \[ \begin{gathered} 1.04^t=\frac{300000\cdot 0.04}{10100}+1=2.188119\\[4pt] t=\frac{\log(2.188119)}{\log(1.04)}=19.965\simeq 20\,. \end{gathered} \] After almost exactly $20$ years, the insured capital is covered. □

Exercise 2.29 The management of a company is facing the decision to acquire a new production facility. The price of the plant is 400,000 GE, it has an expected useful life of 10 years. When the plant is put into operation, it generates a net cash flow of 75,000 GE per year.

Is this investment economically justifiable given the data? For the calculation, assume that the net cash flow is received by the company at the end of each year and consider a discount rate of 5%.

Solution: We calculate the present value of the net cash flows using the formula (2.12). We set \[ \begin{gathered} d=\frac{1}{1.05},\quad a=75000,\quad t=10\,. \end{gathered} \] The calculation yields: \[ \begin{gathered} B=ad\,\frac{1-d^{10}}{1-d}\simeq 579130\,. \end{gathered} \] If now $I=400000$ is the investment sum, then the difference \[ \begin{gathered} B-I=579130-400000 = 179130 \end{gathered} \] represents the capital value of the investment. If this is positive, as in our example, then the investment under consideration is economically plausible, because the payment stream generated by it has a present value which is higher than the disbursement required for the acquisition of the plant. □

Exercise 2.30 Someone offers a house for sale at a price of 420,000 GE. A prospective buyer offers to repay this amount in five equal annual installments $a$, with the first installment being paid immediately and the others at the beginning of the following years. What must the annual installment $a$ be if the calculation is based on an interest rate of 3%?

Solution: The purchase offer represents a pre-due annuity with unknown payment $a$ and a term of five years. The present value of this annuity must be equal to the price at which the house is offered. Therefore, we use formula (2.11) for the pre-due present value and solve for $a$: \[ \begin{gathered} B_t = a\frac{1-d^t}{1-d}\implies a = \frac{B(1-d)}{1-d^t}. \end{gathered} \] By substituting the data from the statement, we obtain: \[ \begin{gathered} a=\frac{420000(1-1/1.03)}{1-1/1.03^5} = 89037.7864\simeq 89038\,. \end{gathered} \] □

Exercise 2.31 A 35-year-old employee wants to save an amount by making consistent annual payments of 50,000 GE, which she always makes at the end of the year, until her retirement in 25 years, which should then be paid out to her for 20 years, starting each year at the beginning of the year, as an additional pension. What is the annual amount of the expected additional pension if an interest rate of 5% is assumed?

Solution: In this task, we deal with two streams of payments:

The savings process (capital accumulation): this represents an annuity payable in arrears with a term of 25 years. The final value of this annuity is the capital formed by this stream of payments.
The supplementary pension (annuity): this stream of payments arises from the consumption of the retirement capital formed during the savings process. It corresponds to an annuity payable in advance with a term of 20 years.

The final value of the payments must be equal to the present value of the disbursements. Let $R$ be the sought-after amount of the supplementary pension, $a=50000$, $q=1.05$ and $d=1/1.05$ denote, as always, the accumulation and discount factor. Using the annuity formulas (2.11) and (2.14), we obtain: \[ \begin{gathered} a\frac{q^{25}-1}{q-1}=R\frac{1-d^{20}}{1-d}\implies R=a\frac{q^{25}-1}{q-1}\cdot\frac{1-d}{1-d^{20}}= 182368.8518\,. \end{gathered} \] The expected amount of the annual supplementary pension is thus approximately 182,369 GE, which is more than 3.6 times the annual savings amount! The reason for the impressive amount of the supplementary pension is by no means the shorter term of the retirement pension. If we repeat the calculation with a term of 25 years for the retirement pension, we get: \[ \begin{gathered} R'=a\frac{q^{25}-1}{q-1}\cdot\frac{1-d}{1-d^{25}}=161254.9972, \end{gathered} \] which is still more than 3.2 times the annual savings amount. This impressive effect is explained by the exponential growth of capital invested with compound interest. □

Example 2.32 (Prices of Bonds, Plain Vanilla Bonds)

A standard bond, Plain Vanilla Bond, is a fixed-interest security issued by states or larger companies to raise funds in the capital market. The issuers (debtors) guarantee the subscribers (creditors) the repayment of a nominal value $N$ after $T$ years as well as fixed coupon payments, coupons $K$, which are paid out in arrears once or several times a year. This generates a payment stream, whose structure is shown in Figure 2.5.

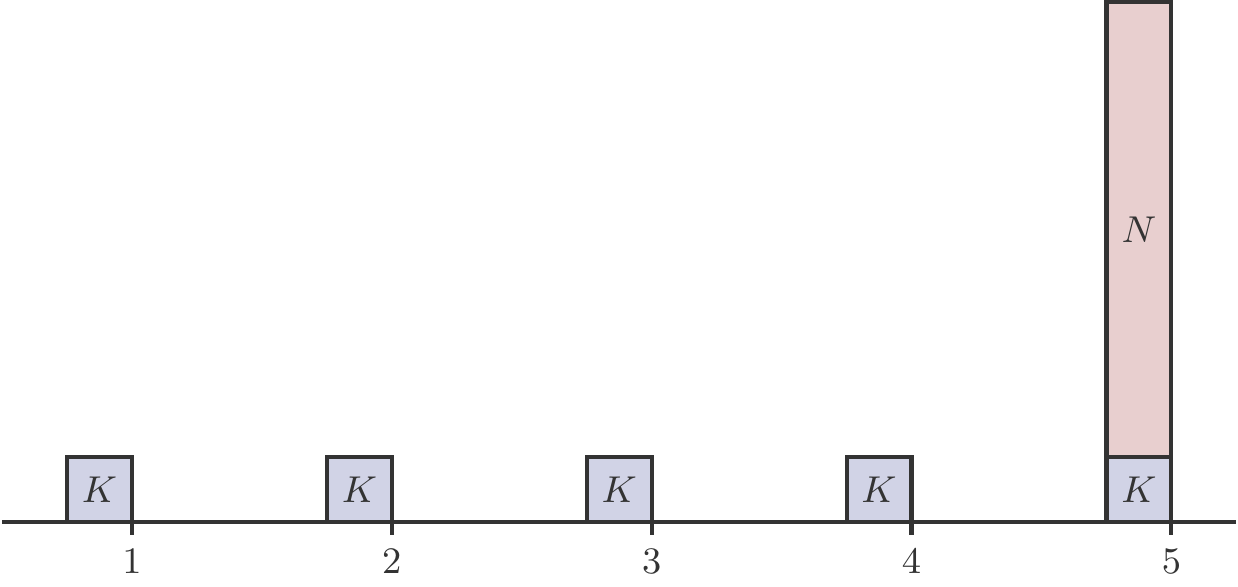
Figure 2.5: Payment stream of a 5-year bond.

The price $P$ of the bond is the present value of this payment stream. This is usually given as a percentage of the nominal value, a size which is called the course of the bond. We calculate the price $P$ using the deferred present value formula (2.12): \[ \begin{aligned} P &= Kd+Kd^2+\ldots+Kd^T+Nd^T\\ &=Kd\frac{1-d^T}{1-d}+Nd^T\,. \end{aligned} \tag{2.16}\]

We now want to perform a specific calculation.

Exercise 2.33 In March 2009, the Republic of Austria issued a bond with the following key data:

\[ \begin{gathered} \begin{array}{ll} \text{Federal Bond 2009-2026/2/144A} \\ \text{ISIN AT 000A0DXC2} \\ \hline \text{Nominal} & 1000 \\ \text{Coupon} & 4.85\: \% \: \text{of the nominal annually} \\ \text{Term}& 17\:\text{years}\\ \end{array} \end{gathered} \]

At the time of issuance (March 2009), the long-term interest rate was 3.94 %. What was the price of this bond?

Solution: The coupon $K$ is calculated from the principal $N=1000$ and the promised interest rate: \[ \begin{gathered} K=0.0485\cdot 1000 = 48.5\,. \end{gathered} \] The discounting is done with the long-term interest rate $r=0.0394$, hence $d=1/1.0394$. Using (2.16), we find the price: \[ \begin{gathered} P=48.5\cdot d\cdot\frac{1-d^{17}}{1-d}+1000\cdot d^{17} = 1111.22 \end{gathered} \] This results in a price of $P/N=1.111$, which is 111.1 %. One also says that the bond is quoted above par.

What if the coupon interest rate had been equal to the market interest rate?

Now the coupon would be $Nr$. But since $d=1/(1+r)$, it follows that \[ \begin{gathered} r = \frac{1-d}{d}\implies K=\frac{N(1-d)}{d}, \end{gathered} \] and the price of the bond would then be (substituting into (2.16)): \[ \begin{gathered} P= \frac{N(1-d)}{d}\,d\,\frac{1-d^T}{1-d}+Nd^T=N, \end{gathered} \] The principal and the price of the bond agree, the bond is then quoted at par. □

The next exercise introduces a new, interesting aspect.

Exercise 2.34 To finance an annuity payable in advance at the amount of $15\,000$ GE, a capital of $200\,000$ GE is available. For how many years can the annuity be paid out if the interest rate is 4%?

Solution: So far, we have interpreted the present value of a payment series (annuity) as the present value of future expected payments. This was the perspective of the beneficiaries, the recipients of the payments. But how does the situation look from the point of view of those who are obliged to make the payments?

For them, the present value of the annuity is the capital that is used to finance the payment stream. All we need to do is consider the representation (2.11) from the position of the party providing the annuity.

Against this backdrop, we now read the stipulation as follows: the annuity capital of 200,000 units of currency is the present value $B_t$ of an annuity-due with payment $a=15,000$ and interest with $r=0.04$. Our task is now to calculate the reference time $T$. To do this, we use the annuity-due present value formula (2.11), which we solve for $T$. We proceed as follows: we first transform (2.11): \[ \begin{gathered} B_T=a\frac{1-d^T}{1-d}\implies d^T=1-\dfrac{B}{a}\cdot (1-d) \end{gathered} \] Substituting the values yields the exponential equation: \[ \begin{gathered} \left(\frac{1}{1.04}\right)^T=1-\frac{200000}{15000} \left(1-\frac{1}{1.04}\right) = 0.487179\,. \end{gathered} \] Using logarithms, we find the solution $T = 18.335278$.

In other words: the annuity capital is sufficient to finance 18 full payments. □

Two interesting questions now arise.

1.) What is the annuity capital at the beginning of the 19th year?

We answer this question more generally: if an annuity capital $K$ is sufficient to fund $T$ payments of amount $a$ upfront, what is the remaining capital $R_T$ at the beginning of year $T+1$?

Since the evaluation point $T$ lies in the future, the remainder $R_T$ results from the future value of the annuity capital $K$ minus the future value of the upfront made payments $a$. Using (2.13): \[ \begin{gathered} R_T=Kq^T-aq\frac{q^T-1}{q-1} \end{gathered} \] Using the data from the last task, in particular $q=1.04$: \[ \begin{gathered} R_{18}=200000\cdot q^{18}-15000\cdot q\cdot\frac{q^{18}-1}{q-1}= 5094.862078\simeq 5095\,. \end{gathered} \] In other words, the remaining capital at the beginning of the 19th year is 5095 units of currency.

2.4.2 Perpetual Annuities

A perpetual annuity is characterized by the fact that the annual payments $a$ are exactly equal to the annual interest income of the annuity capital. This means:

The annuity capital remains unchanged over time;
The payments can be financed without a time limit.

Let us designate $B_\infty$ as the base capital of a perpetual annuity, i.e., its present value. Let’s first examine the ordinary annuity case: at the end of the year, an amount is paid out that is exactly equal to the interest earned that year, i.e., $a=rB_\infty$. Thus, for the present value of an ordinary perpetual annuity: \[ \begin{gathered} B_\infty = \frac{a}{r} = \frac{ad}{1-d}, \end{gathered} \tag{2.17}\] because $d=1/(1+r)$ and therefore $r=(1-d)/d$. If, however, the payments are made annuity-due, then the individual payments $a$ have to be discounted one year less, so we divide (2.17) by $d$: \[ \begin{gathered} B_\infty = \frac{a(1+r)}{r}=\frac{a}{1-d}. \end{gathered} \tag{2.18}\] Classic cases of perpetual annuities are foundations, whose interest income is used to regularly finance certain projects (often charitable). The most famous example is undoubtedly the Alfred Nobel Foundation set up in 1900. It was originally endowed with a capital fund of 31 million Swedish Krona. Today, the foundation capital amounts to approximately 3 billion Krona (350 million Euros).

Apart from this, we encounter perpetual annuities regularly when dealing with time unlimited long-term liabilities, such as indefinite lease and tenancy agreements.

Exercise 2.35 What capital is necessary to finance an upfront perpetual annuity of 1000 units of currency at an interest rate of 8%?

Solution: Using (2.18) we find: \[ \begin{gathered} B_\infty = \frac{1000(1+0.08)}{0.08}= 13500. \end{gathered} \] □

Exercise 2.36 The operator of a supermarket has set up its customer parking on a leased plot of land. The lease contract is unlimited, the annual lease paid at the end of the year for the land is 200,000 units of currency.

The management of the market would like to purchase the property to eliminate the permanent financial burden of the lease payment. With a long-term market interest rate of 4%:

What would be a fair purchase price?
What would be the payable (ordinary) installment if this purchase price is evenly spread over five years?

Solution: Since the lease agreement is indefinite, the lease payments of the company to the owners of the property generate a payment stream that corresponds to a perpetuity payable at the end of each period. Using (2.17) we calculate the fair purchase price as the present value of this annuity: \[ \begin{gathered} B_\infty = \frac{200000}{0.04} = 5\,000\,000\,. \end{gathered} \] The installment payments, let’s call them $R$, form a perpetuity with a present value that results from (2.12). This must be equal to the present value of the perpetual annuity (2.17) with payment $a$. In general, we have: \[ \begin{gathered} \frac{ad}{1-d}=Rd\frac{1-d^t}{1-d}\implies R=\frac{a}{1-d^t}. \end{gathered} \] With our given data: \[ \begin{gathered} R=\frac{200000}{1-(1/1.04)^5} = 1123135.57\,. \end{gathered} \] The annual installment amounts to approximately 1,123,136 GE. □

2.4.3 Consols

Perpetuities are also occasionally used as financing instruments; they are then called consols (from consolidated) or perpetuities.

The concept: The debtor receives capital from the creditor that he never has to repay. In return, the debtor commits to pay interest indefinitely (ad infinitum).

This structure has advantages and disadvantages for creditors:

Advantages: For good debtors, creditors face a long-term stable payment stream.
Disadvantages: Creditors bear the risk of inflation and default risk. The latter because in case of insolvency this debt typically constitutes subordinated capital. These disadvantages are generally compensated by higher interest rates.

The oldest still active perpetuity of 1000 Carolus guilders was issued in 1648 in the Netherlands. At that time, the funds were used to finance a flood defense dike. The bond is still being serviced today (2018), and the coupon amount of the bond is currently 11.34 Euro.

Today, consols are issued by both governments and large corporations. A recent example is the publicly traded Raiffeisen Bank International (RBI). In mid-2017, it issued a perpetual bond for 650 million euros in Poland, with an interest coupon of 6.125%. This bond was oversubscribed threefold within a few hours.

Exercise 2.37 A zero-coupon bond with an issuing volume of 100 million, a maturity of 10 years, and an interest rate of 4% is to be converted into a perpetuity with an interest rate of 6% after 5 years. What amount must be distributed annually (end-of-year) to the subscribers of this bond?

Solution: The price (present value) of the perpetual bond is the 5-year future value of the issuing volume at 4% interest: \[ \begin{gathered} B_\infty = 100\,000\,000\cdot 1.04^5 = 121\,665\,290.24\,. \end{gathered} \] The annual payments are calculated at an interest rate of 6% from (2.17): \[ \begin{gathered} a=r B_\infty=0.06\cdot 121\,665\,290.24 = 7\,299\,917.4144\text{ CU}. \end{gathered} \] One should consider that these payments have to be made ad infinitum while the outstanding debt $B_\infty$ of about 121 million remains unchanged. □

2.5 Sub-annual Interest

In banking, it is common to not only credit interest at the end of the year (i.e., to allow compounding of interest) but also at certain dates during the year. If the year is divided into two interest periods, then interest is compounded semi-annually. For four interest periods per year, we speak of quarterly compounding. The basis for the interest calculation is the nominal annual interest rate $c$. However, this is by no means the return on capital for a whole year, but only a computational size from which the interest rate for the sub-annual compounding is formed.

Let $c$ be the nominal annual interest rate. If the year is divided into $k$ equal interest periods, then the capital is compounded with the interest rate $c/k$ at the end of each period. The nominal annual interest rate is thus evenly distributed across the $k$ compounding periods of a year. A principal amount $K_0$ thus grows over the course of a year to the future value $K_1$: \[ \begin{gathered} K_1=\Big(1+\dfrac{c}{k}\Big)^k\cdot K_0. \end{gathered} \] One can then ask the obvious question of what annual interest rate would achieve the same result. This is an equivalence problem. An equivalent annual interest rate $r$ must produce the same capital $K_1$ after one year and thus satisfy the equation \[ \begin{gathered} 1+r=\Big(1+\frac{c}{k}\Big)^k \end{gathered} \tag{2.19}\] From this follows \[ \begin{gathered} r=\Big(1+\frac{c}{k}\Big)^k-1. \end{gathered} \] $r$ is called the effective annual interest rate.

In practice, introducing sub-annual compounding changes little for us, we just need to adjust the compounding factor accordingly:

Comparison of annual and sub-annual compounding

The future value equation still holds: \[ \begin{gathered} K_t=K_0q^t \end{gathered} \]

Annual compounding with effective interest rate $r$:
$\implies q=1+r$
Compounded $k$ times per year with nominal interest rate $c$:
$\displaystyle\implies q =\left(1+\frac{c}{k}\right)^k$

Exercise 2.38 A principal amount of 10,000 CU is compounded monthly with a nominal annual interest of 4%. What is its future value after 10 years?

Solution: The compounding factor for one year is: \[ \begin{gathered} q=\left(1+\frac{0.04}{12}\right)^{12}. \end{gathered} \] Using the classic future value formula, we obtain: \[ \begin{gathered} K_{10}=K_0q^{10}=10000\left(1+\frac{0.04}{12}\right)^{12\cdot 10}=14908.3268 \text{ ME}. \end{gathered} \] For comparison: if compounded at 4% once per year, the future value would only be: \[ \begin{gathered} K_{10}=10000(1+0.04)^{10}=14802.4428\,. \end{gathered} \] □

Exercise 2.39 A building society compounds loans with a nominal annual interest rate of 6% with quarterly compounding. What is the effective annual interest rate?

Solution: We use (2.19) to calculate the effective annual interest rate: \[ \begin{gathered} r=\Big(1+\frac{c}{k}\Big)^k-1=\Big(1+\frac{0.06}{4}\Big)^4-1=0.06136 \text{ percent}. \end{gathered} \] This corresponds to an effective interest rate of approximately 6.14%. We observe that the effective annual interest rate is higher than the nominal annual interest rate. □

An interesting question is how to calculate the nominal interest rate given an effective annual interest rate and a given number of sub-annual periods. Let’s first look at an example.

Exercise 2.40 A capital is compounded quarterly with an effective interest rate of 8.5%. What is the nominal interest rate?

Solution: Into the basic equation (2.19), \[ \begin{gathered} 1+r = \left(1+\dfrac{c}{k}\right)^k, \end{gathered} \] we enter the given numbers: \[ \begin{gathered} 1+0.085 =\left(1+\dfrac{c}{4}\right)^4, \end{gathered} \] and compute the nominal interest rate $c$ by a simple transformation: \[ \begin{gathered} c=(\sqrt[4]{1.085}\;-\;1)\cdot 4 = 0.0824\,. \end{gathered} \] The nominal interest rate is thus 8.24%. □

In general, it follows that \[ \begin{aligned} \left(1+\frac{c}{k}\right)^k = 1+r &\implies 1+\frac{c}{k}=(1+r)^{1/k}\\ &\implies c=k\left((1+r)^{1/k}-1\right). \end{aligned} \tag{2.20}\]

Exercise 2.41 A credit office wants to offer loans with an effective annual interest rate of 11 percent. However, only the nominal interest rate with monthly compounding is to be published. What should the nominal interest rate be?

Solution: Now $k=12$, and we calculate the nominal interest rate using (2.20): \[ \begin{gathered} c=k\Big((1+r)^{1/k}-1\Big)=12( 1.11^{1/12}-1)=0.1048\,. \end{gathered} \] In other words, the nominal interest rate is 10.48%. □

Exercise 2.42 A capital of 10 000 ME increased to 15 228 ME over 5 years with quarterly compounding. What is the nominal interest rate?

Solution: The following still applies, see the overview (2.19), the future value equation with an appropriately adjusted compounding factor: \[ \begin{gathered} K_5=15228 = 10000\cdot q^5=10000\left[\left(1+\frac{c}{4}\right)^4\right]^5\\[5pt] 15228 = 10000\left(1+\frac{c}{4}\right)^{20}. \end{gathered} \] From this we find: \[ \begin{gathered} 1+\dfrac{c}{4}=\left(\dfrac{15228}{10000}\right)^{1/20} \quad\Rightarrow\quad c=0.085\,. \end{gathered} \] It is therefore compounded at a nominal rate of 8.5%. □

2.6 Exponential Function and Logarithm

2.6.1 Exponential Functions

We can define function expressions by forming powers $a^p$. There are two options for choosing the function variable. When we take the base of the power as the function variable, i.e., form $f(x)=x^p$, a power function arises.

Now we define functions with power terms by using the exponent as the variable; thus, we form $f(x)=a^x$. Such functions are called exponential functions.

Definition 2.43 Let $a>0$. A function with the function term $f(x)=a^x$ is called an exponential function.

Exponential functions are closely related to geometric sequences. If we substitute only the natural numbers $t=1,2,3\ldots$ for the variable $x$, then we get \[ \begin{gathered} f(1)=a,\;f(2)=a^2,\;f(3)=a^3,\ldots,\,f(n)=a^n, \end{gathered} \] which is a geometric sequence with the ratio $a$.

The Figure 2.6 shows typical graphs of exponential functions. From them, we can read the qualitative characteristics of exponential functions, which are listed in the following overview.

Figure 2.6: Graph of $a^x$ for $a>1$ and $0<a<1$.

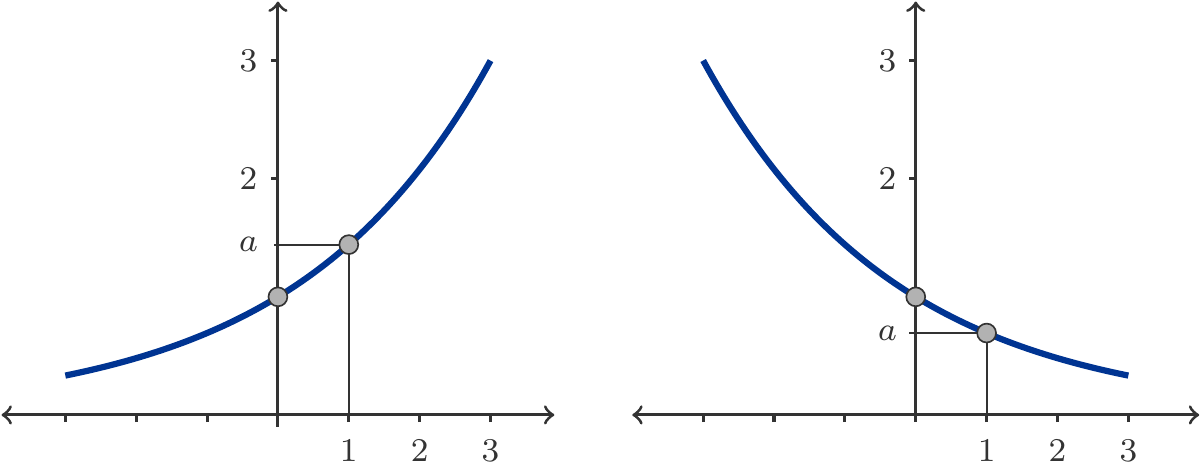
Characteristics of Exponential Functions

An exponential function is defined for all real numbers.
An exponential function only takes positive values.
An exponential function is continuous.
The graph of an exponential function passes through the point $(0,1)$.
The graph of an exponential function passes through the point $(1,a)$.
If $a>1$, then the exponential function is strictly monotonically increasing.
If $0<a<1$, then the exponential function is strictly monotonically decreasing.
An exponential function is bounded on finite intervals, but unbounded on $\mathbb R$.
An exponential function is convex, and its graph is smooth.

What then is the practical significance of exponential functions? To answer this, we examine the relative (percentage) change of an exponential function. Generally, the relative change of a function $f$ over an arbitrary interval $[x,x+1]$ of length 1 is given by \[ \begin{gathered} \frac{f(x+1)-f(x)}{f(x)}. \end{gathered} \] We now consider a function with the term $f(x)=Aa^x$. Apart from the factor $A$, this is an exponential function. Functions of the form $f(x)=Aa^x$ have the remarkable characteristic that their relative change over an interval of length 1 is constant.

For exponential functions, indeed: \[ \begin{gathered} \frac{f(x+1)-f(x)}{f(x)}= \frac{Aa^{x+1}-Aa^{x}}{Aa^x}=a-1 \quad \text{for all $x \in \mathbb R$}. \end{gathered} \tag{2.21}\] If we denote this size with $r:=a-1$, that is, $a=1+r$, then this characteristic property of exponential functions can be expressed as follows:

Theorem 2.44 An exponential function $f(x)=Aa^x=A(1+r)^x$ changes by the same percentage $r$ over intervals of length $1$. In particular, the relative change over such intervals is always the same.

The number $a$ is referred to as the growth factor. If the growth factor $a>1$, then the relative change $r>0$ and the function graph of the exponential function rises monotonically. If, on the other hand, the growth factor $a<1$, then the relative change $r<0$ (relative decrease) and the function graph of the exponential function falls monotonically.

We have observed a similar property in geometric sequences. Exponential functions are the continuous counterpart to geometric sequences. Unlike sequences, they are not confined to discrete points $n=1,2,\ldots$, but can describe a continuous state transition with constant relative growth.

The fact that the relative change of exponential functions is constant underscores their practical significance.

Example 2.45 (Continuous Population Growth)

The annual growth of a biological population is (under ideal living conditions) usually proportional to the size of the population. This means nothing else than that the relative growth per unit of time is constant. Therefore, an exponential function is suitable to describe the growth of the population.

Let $A$ be the initial population size at time $t=0$. The population changes in time intervals of length 1 by the percentage $r$. If we set $a=1+r$, then the size of the population at time $1$ is exactly $f(1)=A(1+r)=Aa^1$. At other times $t>0$, the size of the population is given by $f(t)=A(1+r)^t=Aa^t$.

Exercise 2.46 A population with an initial size of $f(0)=5000$ grows by 12% in total over 10 years. What is the size of the population after 2.5 years? How long does it take for its size to double?

Solution: We must establish the function $f$ that expresses the population size as a function of time $t$. We assume that the population grows continuously at a constant relative rate and therefore the population size can be described by an exponential function $f(t)=Aa^t$.

From $f(0)=Aa^0=5000$ it follows that $A=5000$. Since the population grows by 12% within 10 years, the base $a$ of the desired exponential function is derived from the equation \[ \begin{gathered} f(10)=1.12f(0). \end{gathered} \] It follows that \[ \begin{gathered} \frac{f(10)}{f(0)}=a^{10}=1.12 \implies a=1.12^{1/10}=1.0114. \end{gathered} \] Therefore, the growth function is $f(t)=5000\cdot1.0114^t.$ After 2.5 years, the population has reached the size \[ \begin{gathered} f(2.5)=5000\cdot 1.0114^{2.5}=5143.720687\simeq 5144 \end{gathered} \] For the doubling time, we solve the equation: \[ \begin{gathered} f(t)=10000=5000\cdot 1.0114^t\implies 1.0114^t=2\,. \end{gathered} \] This exponential equation has the solution: \[ \begin{gathered} t=\frac{\log(2)}{\log(1.0114)}=61.148303\simeq 61\text{ years}. \end{gathered} \] □

2.6.2 Continuous Compounding

We investigate how increasingly shortening the compounding periods during the year affects the effective annual interest rate.

The number e (Euler’s number)

First, for the sake of simplicity, we consider a somewhat unrealistic case where we assume the nominal annual interest rate to be $c=100\,\%=1$. With $n$ compounding periods, the compounding factor for one year is therefore: \[ \begin{gathered} q_n=\left( 1+\frac{1}{n} \right)^n. \end{gathered} \tag{2.22}\] We now calculate these compounding factors for 1, 4, 12, etc., compounding intervals per year. The following table contains some terms of the sequence that arises.

\[ \begin{array}{lll} \hline \text{Compounding} & n & (1+1/n)^n \\ \hline \text{annually} & 1 & 2 \\ \text{quarterly} & 4 & 2.44 \\ \text{monthly} & 12 & 2.613 \\ \text{weekly} & 52 & 2.693 \\ \text{daily} & 365 & 2.71457 \\ \text{hourly} & 8760 & 2.7181267 \\ \hline \end{array} \]

The Figure 2.7 shows the graph of the sequence. We have the impression that the sequence $q_n$ increases monotonically and is bounded. Both properties can also be proven mathematically exactly, but we do not want to do this here.

Figure 2.7: The first 12 terms of the sequence $q_n=(1+1/n)^n$.

We are interested in the question of whether the sequence has a limit. If such a limit exists, it has an interesting practical significance. Such a limit then corresponds to the concept of a compounding factor that results from calculating compound interest with infinitely many infinitely small interest periods. This is then referred to as continuous compounding.

However, it is not possible to simply determine a limit by representing it with some kind of transformation of the sequence term as a formula. Rather, the sequence $q_n$ must have a limit due to general mathematical principles³. However, a simple formula for the limit cannot be given. The limit is an irrational number that can only be specified approximately numerically. It is denoted by the letter $e$ and has the value \[ \begin{gathered} e=2.7182818\ldots \end{gathered} \tag{2.23}\] This number $e$ is called Euler’s number. Therefore, it holds that \[ \begin{gathered} \lim_{n\to\infty} \left( 1+\frac{1}{n} \right)^n=e, \end{gathered} \tag{2.24}\] and this number $e$ is the compounding factor for continuous compounding with the nominal interest rate $c=1$.

Definition 2.47 The number \[ \begin{gathered} e:=\lim_{n\to\infty} \Big(1+\frac{1}{n}\Big)^n \end{gathered} \] is called the Euler’s number.

Compound Interest Factors

The practical importance of Euler’s number $e$ in the context of financial mathematics is illustrated by the following considerations.

Let an amount of capital be compounded at a nominal interest rate $c>0$ with $n$ sub-annual periods. The compound factor is \[ \begin{gathered} q_n=\left(1+\frac{c}{n}\right)^n. \end{gathered} \] If we want to apply continuous compounding with the nominal interest rate $c$, we have to let the number $n$ of periods grow to infinity. What happens to the sequence $q_n$ of compound factors?

This sequence is also monotonic increasing and bounded. If we draw the graph, we can understand this. From these two properties we can (with mathematical arguments) conclude that this sequence must be convergent for any choice of $c$ and have a limit. But how do we find this limit?

It is remarkable that the sought limit has a very close relationship with Euler’s number $e$. Specifically, \[ \begin{gathered} \lim_{n\to\infty} \left(1+\frac{c}{n}\right)^n=e^c. \end{gathered} \tag{2.25}\] This formula is so important that we formulate its statement again in words:

Theorem 2.48 If capital is continuously compounded at the nominal interest rate $c$ for a period of one year, then the compound interest factor $q=e^c$.

Since an exact justification of this fact exceeds our means, we convince ourselves of the validity of the formula through numerical experiments (e.g., with a calculator).

Let $c=0.08$. That is, we compound at a nominal interest rate of 8 percent. The following table contains some values of the sequence $q_n$.

\[ \begin{array}{lll} \hline \text{Compounding} & n & (1+c/n)^n \\ \hline \text{annually} & 1 & 1.08 \\ \text{quarterly} & 4 & 1.08234 \\ \text{monthly} & 12 & 1.08300 \\ \text{weekly} & 52 & 1.08322 \\ \text{daily} & 365 & 1.08328 \\ \text{hourly} & 8760 & 1.08329 \\ \hline \end{array} \]

We now compare the compounding factors in the table with the limit from (2.25). It is $e^{0.08}=1.083287\ldots$ This shows an excellent agreement with the prediction of the formula (2.25).

Capital Compounding

Let $K(t)$ be the amount of a capital that is compounded continuously at the nominal interest rate $c$. We know that in this case the compounding factor for one period $q=e^c$ applies, and therefore the capital after one period reaches $K(1)=K(0)q=K(0)e^c$.

However, in continuous compounding, compound interest is credited not only after each full period, but also after every fraction of a period. For example, if $t$ is any arbitrary point in time, then the capital also grows by the factor $q=e^c$ in the time interval $[t,t+1]$, i.e. \[ \begin{gathered} K(t+1)=K(t)q=K(t)e^c. \end{gathered} \] Therefore, the relative growth \[ \begin{gathered} \frac{K(t+1)-K(t)}{K(t)}=\frac{K(t)e^c-K(t)}{K(t)}=e^c-1=:r \end{gathered} \] is constant and $K(t)$ is an exponential function, represented in the form \[ \begin{gathered} K(t)=Aa^t \quad\text{with}\quad a=1+r=e^c=q. \end{gathered} \] From this it follows that $A$ must be $K(0)$ and we finally get \[ \begin{gathered} K(t)=K(0)(1+r)^t=K(0)q^t=K(0)e^{ct}. \end{gathered} \tag{2.26}\] Continuous capital compounding is therefore described by an exponential function with the base $a=1+r=q=e^c$.

Again, we recognize that as with the transition from annual to sub-annual compounding, nothing essential changes. The familiar formula for the future value still applies, only the compounding factor must be adjusted accordingly. Therefore, we add to our summary (2.19):

Comparison of annual, sub-annual and continuous compounding

The future value equation applies: \[ \begin{gathered} K_t=K_0q^t \end{gathered} \]

Annual compounding with effective interest rate $r$:
$\implies q=1+r$
Compounded $k$ times per year with nominal interest rate $c$:
$\displaystyle\implies q =\left(1+\frac{c}{k}\right)^k$
Continuous compounding with nominal interest rate $c$:
$\implies q=e^c$

Exercise 2.49 An amount of 2,500 Currency Units (CU) is continuously compounded at a nominal interest rate of 7.5%. What is the balance after 6 years?

Solution: The compounding factor for one year is $q=e^{0.075}$. Therefore, we get the balance after 6 years by \[ \begin{gathered} K_6=K_0q^6=2\,500\,(e^{0.075})^6=2\,500\,e^{0.45}=3\,920.78. \end{gathered} \] □

Exercise 2.50 Capital is compounded at 7% nominal interest rate. What is the effective interest rate for continuous compounding?

Solution: We denote the nominal interest rate again by $c$ and the effective interest rate by $r$. These quantities are related by the equation $e^{c} = q = 1+r$ in the case of continuous compounding. This leads to the solution of the following equation: \[ \begin{aligned} e^{0.07}& = 1+r \\ r& = e^{0.07} - 1 \\ r& = 0.0725\,. \end{aligned} \] That means, the capital is effectively compounded annually with 7.25%. □

Exercise 2.51 How long must a capital $K$ be continuously compounded at a nominal interest rate of $c=5\,\%$ in order for it to double?

Solution: The compounding factor for one year is $q=e^{0.05}$. The number of periods $n$ must satisfy the inequality $q^t\ge 2$, because we want to double the amount. Therefore, we solve the equation $K_0q^t=2K_0$, that is, \[ \begin{gathered} q^t=(e^{0.05})^t=e^{0.05\cdot t}=2. \end{gathered} \] This exponential equation has the solution \[ \begin{gathered} t=\frac{\log 2}{0.05 \log e}=13.862944\simeq 14. \end{gathered} \] Therefore, the capital needs to be invested for at least 14 periods. □

2.6.3 Logarithm Functions

We are already familiar with logarithms from the section 2.2.1 and the relationship between powers and logarithms. We will now delve deeper into these relationships.

Let us recall the definition of the logarithm from the section 2.2.1. For every positive number $y>0$, there is a logarithm $x=\log y$, characterized by the properties \[ \begin{gathered} \log(10^x)=x \quad\text{and}\quad 10^{\log y}=y \end{gathered} \tag{2.27}\] The logarithm thus reverses the action of the exponential function $y=10^x$, and vice versa. Therefore, we say the function defined by $x=\log y$ is the inverse function to the exponential function $y=10^x$.

Definition 2.52 The function $\log:[0,\infty)\to \mathbb R$, defined by $y=\log x$, is called logarithm function to base 10.

The mention of base 10 in the definition of the logarithm function suggests that there are other logarithm functions as well. However, when we speak of a logarithm function per se, we always mean the logarithm function to base 10 from now on. Here are the most important properties of the logarithm function:

Properties of the Logarithm Function

The logarithm function is defined only for positive numbers.
The logarithm function takes all real numbers as values.
The logarithm function is continuous.
The graph of the logarithm function passes through the point $(1,0)$.
The graph of the logarithm function passes through the point $(10,1)$.
The logarithm function is strictly increasing.
A logarithm function is unbounded near 0 and near $\infty$.
The logarithm function is concave.
The graph of the logarithm function is smooth.

Every exponential function $f(x)=a^x$ is invertible, because it is continuous and strictly monotonic. For the special exponential function $f(x)=10^x$, we already know the inverse function. It is simply the logarithm function $x=\log y$. But what do the inverse functions of exponential functions with a different base look like?

Example 2.53 (Inverses of Exponential Functions)

To invert the exponential function $f(x)=a^x$, we must solve the equation $y=a^x$ for $x$. This is an exponential equation. We take the logarithm of both sides of the equation \[ \begin{gathered} \log y= x \log a, \end{gathered} \] and get the solution \[ \begin{gathered} x=\frac{\log y}{\log a}. \end{gathered} \] The function \[ \begin{gathered} g(y)=\frac{\log y}{\log a} \end{gathered} \] is therefore the inverse function of the exponential function $f(x)=a^x$. It only differs from the logarithm function $x=\log y$ by the multiplication of the factor $1/\log a$.

It is common to refer to the inverse function of any exponential function $f(x)=a^x$ also as a logarithmic function, specifically as the logarithmic function to the base $a$. The notation used is \[ \begin{gathered} \log_a x:=\frac{\log x}{\log a}. \end{gathered} \tag{2.28}\] In this sense, our logarithmic function would be $\log x=\log_{10} x$. However, we do not need logarithmic functions with various bases, since we can solve any exponential equation by using a single logarithmic function. For historical reasons, the logarithmic function to the base of 10 became the standard initially.

2.6.4 Exponential function and natural logarithm

Unfortunately, it is not as simple as it could be. Mathematics and the sciences that apply mathematics have decided to standardize exponential functions and logarithmic functions. But it is not the base 10 that has definitively established itself as the base for scientific applications.

The base 10, which historically led to the introduction of logarithms, is very convenient when using logarithms to perform numerical calculations. For several centuries, this was also the primary application of logarithms. When there were no calculators or computers, multiplications and divisions of numbers with many decimal places were performed with the help of so-called logarithm books, which represented a considerable time saving. Today, this application of logarithms is completely obsolete, and if this were the only application of logarithmic functions, one could simply forget about logarithms.

However, there is another very current (and timeless) application area for exponential functions and their inverse functions, the logarithmic functions. This is the mathematical representation (modeling) of continuous growth processes. We have already encountered examples of this kind at the beginning of this chapter.

If one wishes to set a uniform base for exponential functions and logarithmic functions that is particularly suitable for describing growth processes, then base 10 is by no means mandatory. On the contrary: The fact that humans have ten fingers⁴ has nothing to do with continuous compounding or the growth of biological populations.

So, what would be a reasonable base for exponential functions that are supposed to describe natural continuous growth processes? A number suggests itself, which we already encountered in the context of continuous compounding, namely the Euler’s number \[ \begin{gathered} e=\lim_{n\to\infty} \Big(1+\frac{1}{n}\Big)^n=2.71828\ldots \end{gathered} \] This number has indeed become the uniform base for exponential functions. There are compelling reasons for choosing Euler’s number as the base. We are not yet able to fully understand these reasons at this moment. But we will catch up on this in Chapter 3. For now, let us simply take note of the fact.

Definition 2.54 The function $\exp$ is defined as the exponential function $\exp(x):=e^x$, $x\in\mathbb R$, with the base $e$, where $e$ denotes Euler’s number. This particular exponential function is referred to as the exponential function par excellence.

It is not very convenient to name a specific exponential function as the exponential function without any further attribute, and to hope that the context would always make clear what is meant. It would be better to refer to the function $\exp$ as the natural or Eulerian exponential function. But this is not common practice. On the other hand, the inverse function of $\exp$ is indeed distinguished by a descriptive name.

Definition 2.55 The inverse function of $\exp$ is called the natural logarithm and is denoted by $\ln$.

There is not much need for words regarding the shapes of the graphs of $\exp$ and $\ln$. The Figure 2.8 shows exactly what we expect: the graph of $y=\ln x$ apparently results from reflecting the graph of $y=\exp(x)$ against the line $y=x$.

Figure 2.8: Graph of $f(x)=e^x$ and $f(x)=\ln x$.

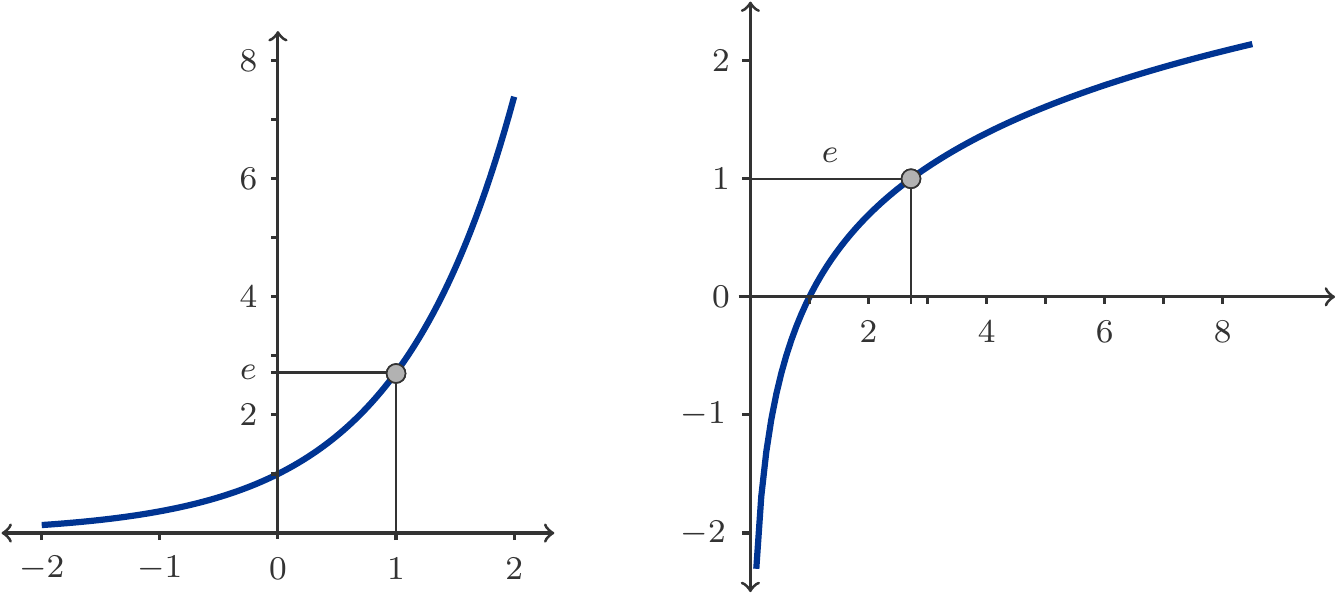
Arithmetic Laws

Example 2.56 (Exponential Function, Natural Logarithm)

Any good calculator allows you to compute $\exp(x)=e^x$. Let’s get accustomed to the function by calculating examples: \[ \begin{gathered} \exp(2)=e^2=7.389056,\qquad \exp(-3.2)=e^{-3.2}=0.040762\,.\\[5pt] \exp(0.0512)=e^{0.0512}=1.052533\,. \end{gathered} \] Clearly, $\exp(1)=e^1=e$. Also, the natural logarithm should be directly available on a good calculator: \[ \begin{gathered} \ln 3=1.098612, \quad \ln 1.5=0.405465, \quad \ln 0.53=-0.634878\,. \end{gathered} \] If that’s not the case, we can also manage by remembering that \[ \begin{gathered} y=e^x\quad\Rightarrow\quad \log y=\log e^x=x\log e \quad\Rightarrow\quad x=\frac{\log y}{\log e} \end{gathered} \] and therefore \[ \begin{gathered} \ln y=x=\frac{\log y}{\log e}=\frac{\log y}{0.434294}=2.302585\,\log y. \end{gathered} \tag{2.29}\] The natural logarithm is therefore approximately 2.3 times the common (base-10) logarithm.

The fact that $\exp$ and $\ln$ are inverse functions means, that one function reverses the action of the other, that is \[ \begin{gathered} (\ln\circ\exp)(x)=\ln(\exp(x))=\ln(e^x)=x,\quad x\in\mathbb R, \end{gathered} \tag{2.30}\] where the symbol $\circ$ represents composition. Furthermore, \[ \begin{gathered} (\exp\circ\ln)(y)=\exp(\ln(y))=e^{\ln y}=y,\quad y>0. \end{gathered} \tag{2.31}\] Questions like $\ln e^2$ or $e^{\ln 5}$ can thus be answered without resorting to a calculator. In particular, $\ln e=\ln e^1=1$.

The calculation rules for arbitrary powers also apply to powers with base $e$, which covers all you need to know about calculating with $\exp(x)=e^x$. The function $\ln$ is, except for a multiplicative factor, identical to $\log$ (see 2.29), so we can calculate with $\ln$ just as we are accustomed to with the logarithm $\log$.

Example 2.57 (Calculation Rules for $\exp$ and $\ln$)

The most important calculation rule for the exponential function is \[ \begin{gathered} \exp(x+y)=\exp(x)\cdot\exp(y). \end{gathered} \tag{2.32}\] It states: Sums are transformed into products. This is clear because \[ \begin{gathered} \exp(x+y)=e^{x+y}=e^x\cdot e^y=\exp(x)\exp(y). \end{gathered} \] Another important rule is the power rule: \[ \begin{gathered} \left(\exp(x)\right)^y =(e^x)^y=\exp(x\cdot y). \end{gathered} \tag{2.33}\] It states: Powers are transformed into products.

The most important calculation rule for logarithms states that products are transformed into sums, i.e. \[ \begin{gathered} \ln (x\cdot y)=\frac{\log (x\cdot y)}{\log e}= \frac{\log x+\log y}{\log e}=\ln x+\ln y. \end{gathered} \tag{2.34}\] When solving exponential equations, we also need \[ \begin{gathered} \ln x^p=p\ln x, \end{gathered} \tag{2.35}\] which can be derived in a completely analogous manner to the corresponding rule for $\log$.

We can therefore solve an exponential equation $a^x=b$ using either common logarithms or natural logarithms: \[ \begin{gathered} x=\frac{\log y}{\log a}=\frac{\ln y}{\ln a}. \end{gathered} \] This is also quite clear, because the logarithmic functions $\log$ and $\ln$ are proportional to one another.

Representation of Exponential Functions

As we have explained at the beginning, the introduction of the exponential function $\exp$ is simply for uniformity. It is customary to convert exponential functions with other bases to the base $e$ and thus represent them using $\exp$. How is this done? How can you convert the exponential function $f(x)=a^x$ to the base $e$?

We proceed by first expressing the base $a$ as a power of $e$, thus according to 2.31 \[ \begin{gathered} a=e^{\ln a}. \end{gathered} \tag{2.36}\] This results in \[ \begin{gathered} f(x)=a^x=(e^{\ln a})^x=e^{x\ln a}. \end{gathered} \tag{2.37}\] We can thus write the function $f(x)=a^x$ in the form $f(x)=e^{cx}$, where we must insert a constant factor $c$, which depends on the original base $a$, namely $c=\ln a$.

We summarize:

Theorem 2.58

There are three different ways to represent an exponential function: \[ \begin{gathered} f(x)=Aa^x=A(1+r)^x=Ae^{cx}. \end{gathered} \]
Here, $a$ denotes the growth factor, $r$ the relative (percentage) change, and $c$ the nominal interest rate.
These quantities are related through \[ \begin{gathered} a=1+r, \quad c=\ln a. \end{gathered} \]

The constant $c=\ln a$ has a substantive significance that is already familiar to us. The following example will demonstrate this.

Example 2.59 (Continuous Compounding)

A capital of $K(0)$ currency units is compounded continuously so that it grows effectively by 12% per year. We want to represent the capital growth as an exponential function using $\exp$.

The relative increase is $r=0.12$ per time unit (year), and therefore the compounding factor (the growth factor) is $q=1+r=1.12$. The exponential function that describes the capital growth is therefore \[ \begin{gathered} K(t)=K(0)\,1.12^t. \end{gathered} \] Now, we want to substitute this representation with a representation in the form $K(t)=K(0)e^{ct}$. To calculate $c$, we form $c=\ln q=\ln 1.12= 0.11333$, and thus we get \[ \begin{gathered} K(t)=K(0)\,e^{t\ln q}=K(0)\,e^{0.11333\,t}=K(0)\exp(0.11333\,t). \end{gathered} \] This is the representation we were looking for.

There is another way. We calculate the nominal interest rate that corresponds to continuous compounding with $r=0.12$. This means, we are looking for a number $c$ such that \[ \begin{gathered} q=1.12=\lim_{n\to\infty} \Big(1+\frac{c}{n}\Big)^n=e^c. \end{gathered} \tag{2.38}\] However, the equation $q=e^c$ is equivalent to $c=\ln q=0.11333$, and we see that it is the same number we calculated above.

Now we understand how to interpret the number $c$ in the representation (2.38): It is nothing other than the nominal interest rate. The two representations of the capital growth by exponential functions with different bases \[ \begin{gathered} K(t)=K(0)\,q^t=K(0)\,e^{ct} \end{gathered} \tag{2.39}\] thus have different interpretations: In the first case, the representation is by the compounding factor $q=1+r$, which is based on the effective interest rate $r$. In the second case, the representation is by the nominal interest rate $c=\ln q$.

Exercise 2.60 What nominal interest rate results in an effective annual interest rate of 10% with continuous compounding?

Solution: Again, we denote the nominal interest rate by $c$ and the effective interest rate by $r$. These quantities are interconnected in continuous compounding by the equation $e^{c} = q = 1+r$. We need to solve this exponential equation: \[ \begin{aligned} e^{c}& = 1.1 \\ c\,\ln\,e& = \ln\,1.1\qquad\qquad (\ln\,e = 1) \\ c& = 0.09531\,. \end{aligned} \] The nominal annual interest rate is therefore about 9.5%. □

Exercise 2.61 What nominal interest rate triples the capital over the course of $15$ years with continuous compounding?

Solution: We denote the nominal interest rate by $c$ and the effective interest rate by $r$. These quantities are interconnected in continuous compounding by the equation $e^{c} = q = 1+r$. Hence, we have \[ \begin{gathered} K(t)=\big(e^{c}\big)^{t}\cdot K(0)=e^{ct}\cdot K(0). \end{gathered} \] The problem statement leads us to the equation \[ \begin{gathered} K(15) = e^{15c}\cdot K(0) = 3\,K(0). \end{gathered} \] From this, we can solve an exponential equation: \[ \begin{aligned} e^{15c}&=3 \\ 15c\,\ln\,e&= \ln\,3\qquad\qquad (\ln\,e = 1) \\ c& = \dfrac{\ln\,3}{15} = 0.073241\,. \end{aligned} \] The nominal annual interest rate is approximately 7.3%. □

Exercise 2.62 After how many years will an initial capital be tripled if it is continuously compounded at a nominal interest rate of 5%?

Solution: We denote the nominal interest rate with $c$ and the effective interest rate with $r$. These quantities are related by the equation $e^{c} = q = 1+r$ with continuous compounding. Therefore, we have \[ \begin{gathered} K(t) = e^{ct} \cdot K(0). \end{gathered} \] The problem statement leads to the equation \[ \begin{gathered} K(t) = e^{0.05t} \cdot K(0) = 3 \cdot K(0). \end{gathered} \] From this, we again obtain an exponential equation that we can solve: \[ \begin{aligned} e^{0.05t} &= 3 \\ 0.05t \ln e &= \ln 3 \qquad\qquad (\ln e = 1) \\ t &= \frac{\ln 3}{0.05} = 21.972246 \approx 22. \end{aligned} \] In 22 years, the capital will have tripled. □

2.7 Additional Exercises

A capital $K_0 = 2000$ currency units grows through simple interest over the course of 10 years to a final value of 6000 currency units. What was the interest rate?

Solution: 20 %
A capital $K_0$ grows with 3.5% compound interest and over 12 years reaches a sum of 18 208 currency units. Calculate $K_0$. Round the result to a whole number.

Solution: $K_0 \approx 12 050$ currency units
Someone receives two purchase offers for their condominium, Offer A: 200 000 immediately in cash. Offer B: 220 000 currency units, but only in two years’ time. Which offer is better if the market interest rate is 5%?

Solution: Present value $A = 200\,000$, present value $B = 199 546$, A is better.
A capital of 19 000 currency units is invested at 11.53% interest for 14 years. After 5 years, the interest rate is reduced, so that the effective interest rate for the total period only amounts to 9.916%. Calculate the new interest rate after the reduction.

Solution: 9.02 %
A father invests a capital amount at a bank for his currently nine-year-old daughter to provide her with a starting capital of 171 000 currency units for her 24th birthday. Five years after the deposit, the bank reduces the interest rate to 3% and the father has to pay an additional amount of 36 143.91 currency units at this time to secure the final sum. What was the initial interest rate granted by the bank?

Solution: 6.5 %
Ms. C grants her nephew a loan of 12 000 currency units to finance his studies. This loan is to be paid back with 5% interest annually and is to be repaid with interest and compound interest as soon as the nephew graduates. In fact, the nephew pays back Ms. C a sum of 16 885 currency units. How long did he take for his studies? Round the result to the nearest whole number greater.

Solution: 7 years
Zero-coupon bonds are being offered with a face value (redemption value) of 1000 currency units, guaranteed interest of 4.5% and a term of 10 years. At what price?

Solution: 643.93 currency units
A Zero Bond with a face value of 10 000 currency units and a term of 5 years is being offered for a price of 8 600 currency units. Currently, the market interest rate is 3.75%. Is this investment sensible?

Solution: No, the interest rate of the bond is only 3.06%.
Someone enters as a silent partner (lender) with an amount of 100000 currency units in a company. After 5 years, the partner receives 137000 currency units back for his investment. During the 5 years, neither interest nor repayment were made. Calculate the annual return on investment.

Solution: 6.5 %
A community invests a capital at 10.5% interest, which is to grow to 21 million currency units in 20 years and then to be used for the construction of a seniors’ home. After 11 years, the bank has to reduce the interest rate. In order to still reach the required final sum within the set time, an amount of 1 955 372 is added. How much has the interest rate been reduced?

Solution: 2.5 %
Ms. X has taken out a non-amortizing loan from a private loan agency, which is to bear interest at 17.3%. Her lawyer advises her to sue in court because of the high interest rates. The court rules in her favor and reduces the interest rate to 7.1%. As a result, the repayment sum was reduced from 93 712 to 651̇27 currency units. What was the agreed term of the loan in years?

Solution: 4 years
Albrecht von Wallenstein, Duke of Friedland, granted Emperor Ferdinand II a loan in 1628, for which he demanded 28% interest. Under pressure from Prince Harrach, who found this interest rate indecent, Wallenstein voluntarily reduced the interest rate to 10%. This resulted in Ferdinand II having to repay only 5710 instead of 10469 guilders. What was the loan amount and for how many years had it been granted?

Solution: $t=4, K_0=3900$
A machine with an operational life of 5 years costs 307 000 currency units and the annual operating costs are 15 350 currency units. What annual return (deferred) must the machine produce if its purchase is not to be a loss and if 7% compound interest is calculated? Round the result to a whole number.

Solution: 90224 currency units
An insurance company insures 930 000 currency units against the payment of an annual premium of 8 120 currency units in advance. After how many years is the insured capital covered at 6.5% compound interest? Round the result to a whole number.

Solution: 33 years
A capital sum of 10,070,000 CU earning 10% interest per annum is to be used for the payment of an annuity due. What is the maximum annual payment so that the annuity can be paid out for at least 10 years? Round the result to a whole number.

Solution: 158,307 CU

The construction of a highway costs $600$ million GE, with an annual maintenance cost (advanced) of $15 million estimated. These costs should be covered by the sale of annual vignettes. What should the price for an annual vignette be set at if, on average, $400,000$ cars are expected each year, and the invested capital with an interest rate of $5$% is to be repaid in $25$ years?

Solution: $138.9$ CU

An individual makes an annual deposit at the beginning of each year into a savings account to finance a trip worth 44,000 CU after 7 years. What is the minimum deposit that must be made if the interest rate is 5.5% per annum? Round the result to a whole number.

Solution: 5,045 CU

A capital of 120,000 CU is available for the financing of an annuity due amounting to 11,000 CU. For how many years can the annuity be paid out if the interest rate is 5%?

Solution: 15 years

A plain vanilla bond is offered with a face value of 10,000 CU, a term of 15 years, and an annual coupon of 530 CU, payable at the end of each year. The long-term market interest rate is 4.2%. What is the issue price for this bond?

Solution: $P=11,206.10 CU

A capital is nominally earning interest at 7%. After how many years has the capital doubled if the compounding occurs semi-annually with 6 compounding periods per year?

Solution: $t=9.96 \approx 10$ years

It is known that two brothers, who inherited 600,000 CU ten years ago, now have a total of 862,100 CU. How much did one inherit and how much the other if the first invested his money at 4% with annual compounding, and the second invested his share at 3.5% with semi-annual compounding?

Solution: 202,136.44 CU and 397,863.56 CU, respectively

A capital of 38,000 CU is continuously compounded at an interest rate of 9.3%. How much is the capital after 5 years?

Solution: 60,496.54 CU

In what time period does an initial capital double if it is continuously compounded at a nominal interest rate of 4.8%?

Solution: 14.44 years

A capital $K_0$ GE is continuously compounded such that it effectively grows by 7 percent per year. Calculate the nominal interest rate.

Solution: 6.77%

What nominal interest rate doubles a capital in the course of 16 years with continuous compounding?

Solution: 4.33%

A capital is nominally compounded at 11.5 percent interest. What is the effective interest rate with continuous compounding?

Solution: 12.19%

A lends B a loan of 100,000 CU. B agrees to repay the debt in two instalments: 55,000 CU at the end of the first year, and another 55,000 CU at the end of the second year. At what interest rate was the loan made?

Solution: 6.6%

Sometimes the interest rate is given as a percentage. This merely means that a different unit of measurement is used. In the case of percentages, these are hundredths. An interest rate of 8 percent means an interest rate $r=0.08$. Often, the interest rate is denoted by the letter $i$ (interest). However, since the letter $i$ is frequently used for other purposes in mathematics, we will not denote interest rates with $i$.↩︎
In Theorem 2.22, the term of the general element is the term of an exponential function. We will delve into exponential functions in more detail later.↩︎
Indeed, the existence of the limit is a consequence of the monotonicity and boundedness of the sequence $q_n$.↩︎
That is surely the historical root of the decimal system.↩︎