5  Probability

5.1 Basic Concepts

5.1.1 Random Experiments and Sample Space

At the beginning of our considerations, we introduce the concept of an experiment. By this, we understand a process that is conducted under precisely defined conditions and produces a result that can be observed.

Every experiment that has at least two possible outcomes, we call a random experiment. Or to put it another way: any experiment that, if repeated under the same conditions, does not always yield the same result, is not a random experiment.

The essence of a random experiment is the fundamental unpredictability of its outcome. This raises the immediate question: how can one develop a mathematical theory for processes that exhibit this very property of unpredictability?

The answer lies in repetition. When a random experiment is repeated many times, patterns begin to emerge gradually that eventually solidify into laws, laws that are not only of extraordinary beauty and aesthetics but also allow for predictions of breathtaking accuracy.

To mathematically describe a random experiment, we need some basic concepts. We begin with:

Definition 5.1 (Sample Space) The sample space \(\Omega\) of an experiment is the set of all possible outcomes an experiment can have.

Another basic concept is that of an event.

5.1.2 Events

Definition 5.2 (Event) An event is a statement about a possible outcome of a random experiment. Thus, every event corresponds to a subset of the sample space, namely, the subset of outcomes for which the statement is true.

It is customary to denote events by Latin capital letters, preferably from the first half of the alphabet, e.g., \(A\), \(B\), etc.

To better understand the concept of an event, let us look at an example.

Exercise 5.3 A random experiment consists of throwing a regular six-sided die, whose sides are numbered \(1,2,\ldots,6\), exactly one time. Represent the event {I roll an even number} as a subset of the sample space \(\Omega\).

Solution: The sample space is \(\Omega=\{1,2,\ldots,6\}\). The event {even number} corresponds to the subset \(A=\{2,4,6\}\). If one rolls a number (e.g., the number 2) that is contained in the subset \(A\), then the event \(A\) has occurred. □

In this task, the sample space was relatively small, so we could easily express \(\Omega\) as a list.

Very often, however, the sample space contains an enormous number of elements, so that it is no longer sensible or even possible to list \(\Omega\). But this is not usually necessary, as we are mostly interested in the size or cardinality of this set, which we denote by \(|\Omega|\).

Exercise 5.4 In a lottery, tickets numbered \(1,2,\ldots,45\) are offered for drawing. The drawing consists of selecting a sample of \(6\) tickets (consecutively and without replacement). Determine the extent of the sample space and that subset which corresponds to the event {jackpot}.

Solution: The sample space \(\Omega\) is the set of all lists (ordered sets) of length six that can be formed from the numbers \(1,2,\ldots,45\).

How many elements does \(\Omega\) contain? It is simple: for the first drawing, we have 45 options, for the second only 44, because the drawing is conducted without replacement. Hence, for each subsequent drawing, the number of possibilities diminishes by one. In total, we have: \[ \begin{gathered} |\Omega|=45\cdot 44\cdot 43\cdot 42 \cdot 41 \cdot 40=5\,864\,443\,200 \end{gathered} \] possibilities. In this lottery, a bet consists of indicating a set of 6 numbers. This bet is then the jackpot if the numbers of the bet, aside from the order, match the results of the drawing. The event \(A=\{\textit{jackpot}\}\) therefore corresponds to the subset \(A\subseteq\Omega\), which consists of all permutations of the drawn betting sequence. This subset \(A\) contains \[ \begin{gathered} |A|=6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1=6! = 720 \end{gathered} \] elements. We see that, in comparison to \(\Omega\), \(A\) is a very small set and therefore we expect that the event \(A\) will be observed rather seldom in the experiment. □

Random Variables

In many cases, events are defined by random variables. A random variable \(X\) is a random number observable during the random experiment. Mathematically, a random variable \(X\) is a function (assigning rule) that assigns a number \(X(\omega)\) to every possible outcome \(\omega\in\Omega\) of the random experiment. Any statement about the random variable is an event. The great advantage of random variables is that we can calculate with them. We can add them, multiply them, etc.

Exercise 5.5 A die with the numbers \(1,2,\ldots,6\) is thrown twice. Let \(X\) be the number rolled on the first throw, \(Y\) the number on the second throw. Determine the subset of the sample space corresponding to the event \(\{X+Y<4\}\).

Solution: In this experiment, the set of outcomes \(\Omega\) consists of all pairs \((a,b)\) that we can form from the numbers \(1,2,\ldots,6\): \[ \begin{gathered} \Omega=\{(1,1),(1,2),\ldots,(6,6)\},\quad |\Omega|=36. \end{gathered} \] Then, we have \[ \begin{gathered} \{X+Y<4\}=\{(1,1),(1,2),(2,1)\},\quad|\{X+Y<4\}|=3. \end{gathered} \] □

5.1.3 Combination of Events

We have already established that events are subsets of the set of outcomes \(\Omega\). Since every set contains the empty set \(\varnothing\) and itself as a subset, that is, \(\varnothing\subset \Omega\) and \(\Omega\subset \Omega\), \(\varnothing\) and \(\Omega\) are also events, albeit of a special kind:

• \(\varnothing\) is the impossible event, because the experiment necessarily must have a result that lies within \(\Omega\).

• \(\Omega\) is the certain event, because \(\Omega\) contains all possible outcomes.

As we know, new sets which are themselves events can be formed from subsets of \(\Omega\) through simple set operations.

Figure 5.1: Combinations of events.

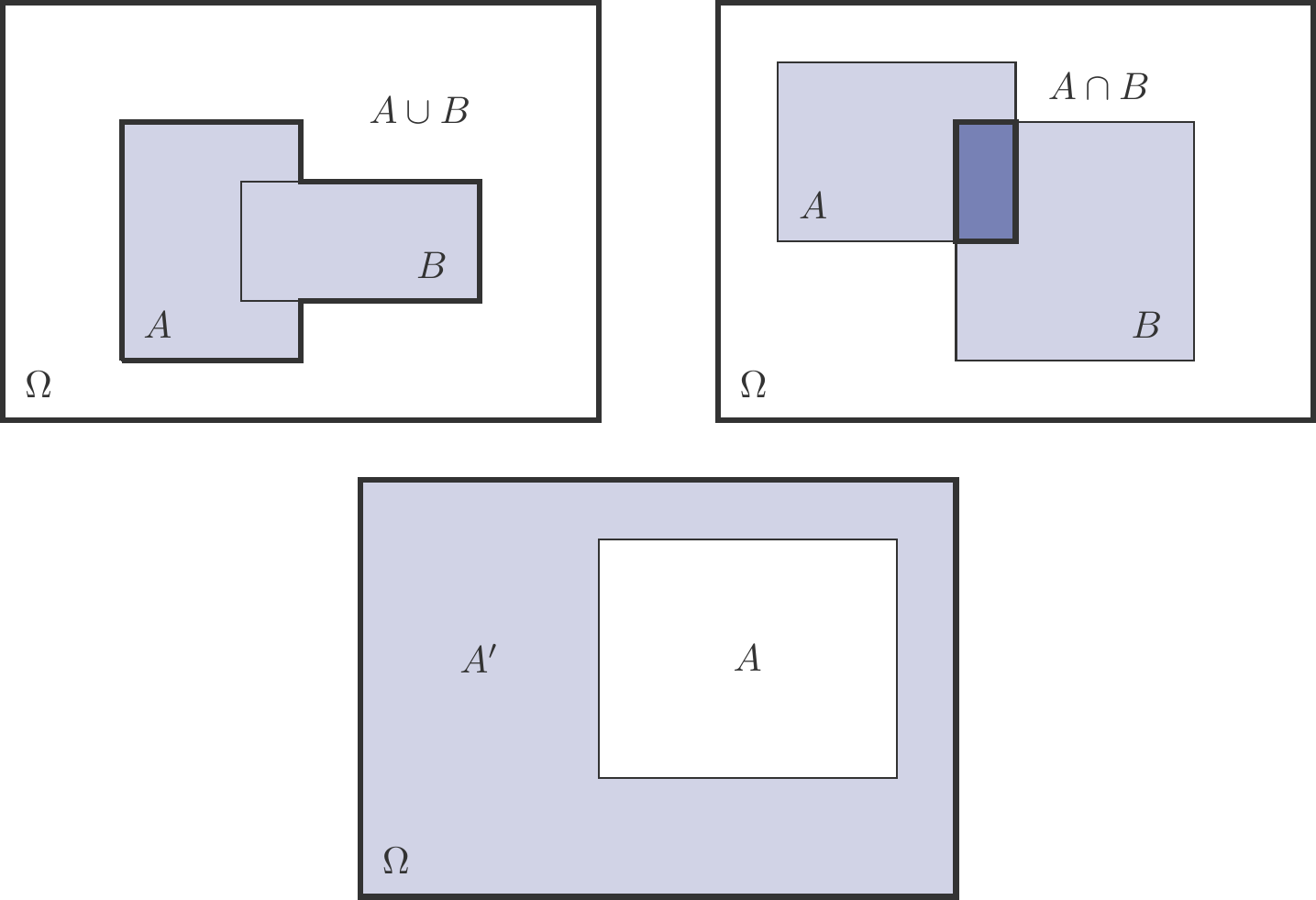
The most important set operations and their interpretations are (see Figure 5.1):

• \(A\cup B\) – the union of two sets
  This is the set of all elements that belong to \(A\) or \(B\). Interpreted as a random event: Event \(A\) or \(B\) occurs.

• \(A\cap B\) – the intersection of two sets
  This is the set of all elements that belong to both \(A\) and \(B\). Interpreted as a random event: Both events \(A\) and B occur.

• \(A'\) – the complement of a set
  This is the set of all elements that do not belong to \(A\). As a random event, the complement is interpreted as: the event \(A\) does not occur.

An important special case occurs when \(A\cap B=\varnothing\). In this case, we say that the two events \(A\) and \(B\) are incompatible; they exclude each other. In short, \(A\cap B\) cannot occur.

For example, consider the experiment of rolling a die once and let \[ \begin{gathered} A=\{\text{even number}\}=\{2,4,6\},\quad B=\{\text{odd number}\}=\{1,3,5\}. \end{gathered} \] Then, \(A\cap B=\varnothing\) because it is not possible when rolling a die once to obtain a number that is both even and odd at the same time.

Example 5.6 (Gambling)

In a gambling game, a series of \(n\) individual games is played, with each individual game having the possible outcomes win (\(G\)) and loss (\(V\)). Therefore, the set of outcomes \(\Omega\) for the series of games consists of all lists of length \(n\) that can be formed from the two letters \(G\) and \(V\). It contains \(|\Omega|=2^n\) lists.

This is easy to understand: each list has \(n\) positions, and for each position we have two options for filling it, namely \(G\) or \(V\). Hence, the number of different lists is \(2^n\).

Let \(S_n\) be the frequency (number) of occurrences of the letter \(G\) in the outcome \(\omega\in \Omega\). Then \(S_n\) is a random variable with possible values \(0,1,\ldots,n\). This random variable indicates the number of wins in the series of games.

The event {at least \(k\) wins} can be symbolically represented by \(\{S_n\ge k\}\). It corresponds to the set of all lists \(\omega\in \Omega\) that contain the letter \(G\) at least \(k\) times.

Exercise 5.7 In a gambling game, a series of \(5\) individual games is played, each of which has the possible outcomes {win} (\(G\)) and {loss} (\(V\)). What is the proportion (percentage) of series in which exactly one win occurs?

Solution: \(\Omega\) is the set of all 5-lists that we can form from the letters \(G\) and \(V\), thus \(|\Omega|=2^5=32\). Let \(A=\{\mathit{exactly~one~win}\}\).

Then \(|A|=5\), because only these 5 lists in \(\Omega\) contain exactly one letter \(G\): \[ \begin{gathered} \mathit{GVVVV},\quad\mathit{VGVVV},\quad \mathit{VVGVV},\quad \mathit{VVVGV}, \quad\mathit{VVVVG}. \end{gathered} \] Therefore, the proportion is \(5/2^5=0.15625\), which is 15.625%. □

The percentage just calculated is our first example of a probability.

5.1.4 Probabilities

Suppose a random experiment with the outcome set \(\Omega\) is given. It is said that an event \(A\) has occurred if, after conducting the random experiment, the realized outcome \(\omega\) is contained in the subset \(A\subseteq\Omega\). This means nothing else than that the statement corresponding to the event \(A\) about the outcome is accurate.

It is fundamentally unpredictable before a random experiment is performed whether a particular event will occur or not. Nonetheless, it is usually the case that after numerous repetitions of the random experiment, some events have occurred more frequently than others. Therefore, it makes sense to use the statistical frequency of occurrence of events as a basis for constructing the concept of the probability of an event.

Definition 5.8 Let \(f_n(A)\) be the relative frequency at which the event \(A\) occurs in a series of \(n\) repetitions of the random experiment. The idea now is that this relative frequency approaches a fixed percentage as the number of repetitions increases: \[ \begin{gathered} \lim_{n\to\infty} f_n(A)=:P(A). \end{gathered} \tag{5.1}\] This limit \(P(A)\) of the relative frequencies is called the probability of \(A\).

This intuitive explanation of the concept of probability just mentioned is not a definition in the mathematical sense. It is merely an assumption that is supposed to make it possible to empirically grasp the theoretical concept of probability. One could refer to this assumption as the empirical law of large numbers. The usefulness of this assumption has been demonstrated by the fact that the mathematical probability theory (stochastic) based on it can make valid statements about real-world applications.

Figure 5.2: Relative frequency for heads from 200 coin tosses.

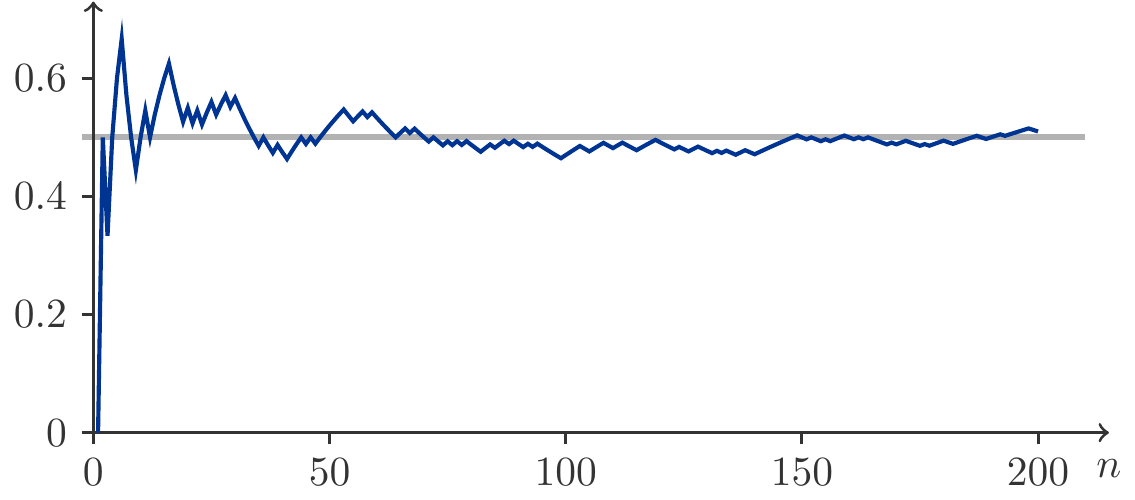
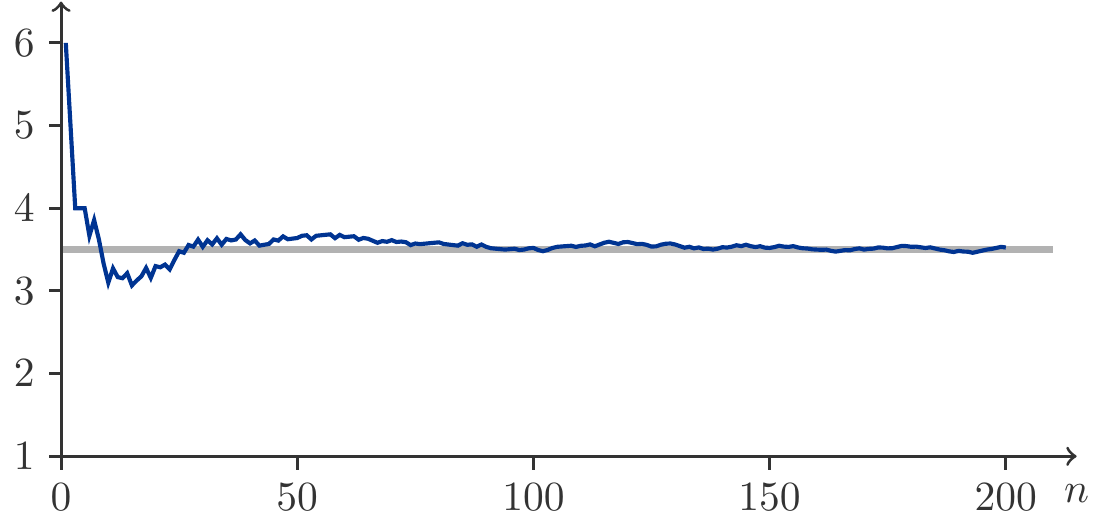
For Figure 5.2, 200 coin tosses were simulated. We see how the relative frequency \(f_n(A)\) of the event \(A=\{\mathit{heads}\}\) approaches the value \(1/2\).

From the intuitive explanation of the concept of probability, we derive the fundamental properties of probabilities:

Theorem 5.9 (Properties of Probabilities) Let \(\Omega\) be the outcome set of a random experiment, and let \(A\), \(B\), \(C\),… be observable events. Then the following laws apply to the probabilities of the events:

1. \(0\le P(A) \le 1\).

2. \(P(\Omega)=1\): The certain event has a probability of 1.

3. \(P(\varnothing)=0\): The impossible event has a probability of 0.

4. If \(A\cap B=\varnothing\), meaning the events \(A\) and \(B\) are mutually exclusive, then the addition law applies: \[ \begin{gathered} P(A\cup B)=P(A)+P(B). \end{gathered} \tag{5.2}\]

The Law of Addition is the most important rule for calculating probabilities.

The numerical determination of probabilities using the Law of Large Numbers (Definition 5.8) often involves significant effort. However, there are situations where we can achieve our goal more easily. To do so, two conditions must be satisfied.

Definition 5.10 (Classical Probability Concept) If

• \(\Omega\) is a finite set, and

• all outcomes of the experiment are equally likely,

then for all events \(A\subset \Omega\): \[ \begin{gathered} P(A)=\frac{|A|}{|\Omega|}=\frac{\text{Number of favorable cases}}{\text{Number of possible cases}}\,. \end{gathered} \tag{5.3}\]

It can be shown that the classical concept of probability possesses all the properties required by Theorem 5.9. However, whether the conditions of Definition 5.10 are met must be checked on a case-by-case basis. The hypothesis of equal likelihood in particular is often critically viewed. Nevertheless, statistics provide methods that allow testing this hypothesis.

If all conditions are met, then determining probabilities with Definition 5.10 is in principle simple. We just need to determine the sizes (cardinalities) of the set of possible outcomes \(\Omega\) and the events \(A\), \(B\), etc. we are interested in by counting.

Exercise 5.11 A die is thrown once. What is the probability of getting an even number?

Solution: We have already established: \[ \begin{gathered} \Omega=\{1,2,3,4,5,6\},\quad |\Omega|=6;\qquad A=\{2,4,6\},\quad |A|=3. \end{gathered} \] From (5.3) it follows that: \[ \begin{gathered} P(A)=\frac{|A|}{|\Omega|}=\frac{3}{6}=\frac{1}{2}. \end{gathered} \] This result is valid under the assumption that the die is fair, i.e., the hypothesis of equal likelihood is fulfilled.

We could also approach the problem experimentally by invoking the empirical Law of Large Numbers (5.1). To do this, it would be necessary to throw the die very often, perhaps a few thousand times, and count how often an even number appears. The relative frequency should be close to \(0.5\) with an increasing number of trials. We expect a graph very similar to Figure 5.2. □

Exercise 5.12 What is the probability of hitting the jackpot in the lottery 6 out of 45?

Solution: In the solution of Exercise 5.4 we have already found: \[ \begin{aligned} |\Omega| & =45\cdot 44\cdot 43\cdot 42\cdot 41\cdot 40=5\,864\,443\,200,\\ |A| & =6!=720,\\ \implies P(A) =\frac{|A|}{|\Omega|} & =\frac{720}{5864443200} =0.0000001227738\,. \end{aligned} \] □

The interpretation of probability as the long-term expected proportion of realizations enables an estimation of the number of realizations in a large series of trials.

Exercise 5.13 In Austria, it is estimated that 8.5% of insurance claims reported to insurance companies are fraudulent or manipulated across all sectors. How many fraud cases per year should an insurance company expect to deal with if it processes 150,000 claims per year?

Solution: Let \(N=150000\) be the number of insurance claims per year and \(p=0.085\) the percentage of fraudulent insurance claims. The expected frequency of fraud cases per year is \[ \begin{gathered} Np=150\,000\cdot 0.085= 12750. \end{gathered} \] □

Exercise 5.14 A company is giving away a vacation trip to one of its 8000 customers through a scratch game. In this scratch game, exactly three correct squares out of ten must be scratched off to win. How many winners of the vacation trip should the company expect?

Solution: Let’s assume that the participants scratch off the fields completely at random. This means all \(10\cdot 9\cdot 8=720\) possibilities of scratching off three fields in a row have the same probability \(1/720\). There are \(3\cdot 2\cdot 1=6\) ways to hit the three correct fields in a different order. Thus, when scratching a scratch card, the event \(A=\{\textit{Winning the vacation trip}\}\) has the probability \[ \begin{gathered} P(A)=\frac{6}{720}=0.00833. \end{gathered} \] With \(N=8000\) participants, one would therefore expect \(N\cdot P(A)= 8000\cdot 0.00833=66.67\approx 67\) winners. □

5.1.5 A Generalization of the Addition Law

The addition law (5.2) allows us to calculate the probability of \(A\) or \(B\) occurring if the events \(A\) and \(B\) are incompatible, meaning \(A\cap B=\varnothing\). However, if \(A\) and \(B\) are not incompatible, then a more general formula applies: \[ \begin{gathered} P(A\cup B)=P(A)+P(B)-P(A\cap B). \end{gathered} \tag{5.4}\] An intuitive explanation is provided by looking at Figure 5.3.

Figure 5.3: The general addition law.

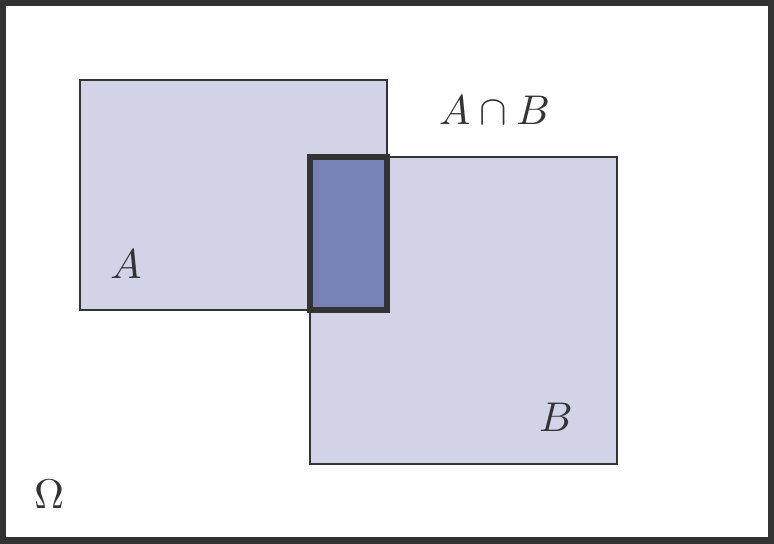
To determine the probability that \(A\) or \(B\) occurs, we cannot simply add the probabilities of \(A\) and \(B\) because generally \(A\cap B\ne \varnothing\). Then the outcomes that belong to \(A\) and \(B\) would be counted twice, so we must subtract \(P(A\cap B)\) once. This is exactly the statement of (5.4).

Exercise 5.15 (Solving a mathematical problem) Student \(A\) solves a mathematical problem with a probability of \(3/4\), while student \(B\) does so with only a probability of \(1/2\). The probability that both solve the problem is \(3/8\).

What is the probability that the problem gets solved?

Solution: From the given information: \(P(A)=\dfrac{3}{4},\; P(B)=\dfrac{1}{2}, \;P(A \cap B)=\dfrac{3}{8}\).

If the problem is solved, it means: \(A\) solves the problem, or \(B\) manages to solve it, or both succeed.

We are thus looking for \(P(A\cup B)\). Using the addition law (5.4): \[ \begin{aligned} P(A\cup B)&=P(A)+P(B)-P(A\cap B)\\ &=\frac{3}{4}+\frac{1}{2}-\frac{3}{8}=\frac{7}{8}=0.875\,. \end{aligned} \]

5.1.6 Random Variables

Probabilities for events expressed by random variables can be calculated in a similar way. The law of large numbers (5.1) is available to us, just like the classical concept of probability (5.3).

Exercise 5.16 A die is rolled twice. Let \(X\) be the result of the first roll and \(Y\) the result of the second roll. What is the probability that \(P(X+Y<4)\)?

Solution: Since all \(6\cdot 6=36\) possible outcomes (eye pairs) of \((X,Y)\) are considered equally likely, each has the probability \(1/36\). There are exactly 3 outcomes whose sum of eyes is less than 4, namely \[ \begin{gathered} \{X+Y<4\}=\{(1,1),(1,2),(2,1)\}. \end{gathered} \] Therefore, \[ \begin{gathered} P(X+Y<4)=\frac{3}{36}=0.0833\,. \end{gathered} \]

Exercise 5.17 A die is rolled twice. Let \(X\) be the result of the first roll and \(Y\) the result of the second roll. What is the probability that \(P(X-Y=0)\)?

Solution: The sample space \(\Omega\) is the set of all 36 pairs \((a,b)\) where \(a,b=1,\ldots 6\). The event \(\{X-Y=0\}\) can only occur if \(X=Y\). There are exactly 6 possibilities: \[ \begin{gathered} \{X=Y\}=\{(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)\}. \end{gathered} \] Therefore, \[ \begin{gathered} P(X-Y=0)=\frac{6}{36}\approx 0.1667\,. \end{gathered} \] □

Theorem 5.18 (Theorem of the Complementary Event) Let \(A\) be an event, then it follows: \[ \begin{gathered} P(A')=1-P(A). \end{gathered} \tag{5.5}\]

Justification: The event \(A\) and its complement \(A'\) are certainly incompatible, i.e., \(A\cap A'=\varnothing\). On the other hand, their union constitutes the sample space \(\Omega\), so \(\Omega=A\cup A'\). Thus, from the addition rule (5.2): \[ \begin{gathered} P(\Omega)=1=P(A)+P(A')\implies P(A')=1-P(A). \end{gathered} \] □

We consider a game of chance consisting of a series of individual games, each with possible outcomes \(G\) (win) and \(V\) (loss). Such a game is called symmetric if, in each individual game, winning and losing are equally probable and if the results of one game do not influence the results of another. Under these conditions, all \(2^n\) possible lists of results have the same probability \(1/2^n\).

Exercise 5.19 A player participates in a symmetric game of chance and plays 10 times. What is the probability that they will win at least once?

Solution: Let \(S_{10}\) be the number of wins in a series of 10 games. What is \(P(S_{10}\ge 1)\)?

To determine this, we consider the complement of \(\{S_{10}\ge 1\}\). What is the opposite of {at least one win in 10 games}?

It’s simple: \(\{S_{10}\ge 1\}'=\) {no single game was won out of 10 games}!

Hence \(\{S_{10}\ge 1\}'=\{S_{10}=0\}\) and therefore, by (5.5): \[ \begin{gathered} P(S_{10}\ge 1)=1-P(S_{10}=0). \end{gathered} \] However, the probability on the right-hand side is easy to determine because the underlying event corresponds to only a single outcome, namely losing all 10 games. This happens with probability \(1/2^{10}\). It follows that \[ \begin{gathered} P(S_{10}\ge 1)=1-\frac{1}{2^{10}}=0.9990234\,. \end{gathered} \] □

Exercise 5.20 A player participates in a symmetric game of chance. Let \(W\) be the waiting time (number of individual games) until the first win. Calculate \(P(W\le 8)\).

Solution: Again, we argue with the complement. It is \[ \begin{gathered} P(W\le 8)=1-P(W>8). \end{gathered} \] But if the event \(\{W>8\}\) has occurred, then we know something about the outcome of the first 8 games: \(W\) can only be \(>8\) if not a single game was won out of the first 8 games. Otherwise, \(W\le 8\). In other words: \[ \begin{gathered} P(W\le 8)=1-P(W>8)=1-P(S_8=0)=1-\frac{1}{2^8}=0.9961\,. \end{gathered} \]

Exercise 5.21 (A Paradox) What is the probability that in a group of 10 people at least two have a birthday on the same day (regardless of the year)?

Solution: We represent a birthday by a natural number between 1 and 365. That is, 1 corresponds to January 1st, and so on. The result set \(\Omega\) is the set of all possible lists of 10 numbers from \(1,2,\ldots,365\). And of course, birthdays can occur multiple times. It could be that all 10 people have their birthday on January 1st. The cardinality of \(\Omega\) is therefore: \[ \begin{gathered} |\Omega|=\underbrace{365\cdot 365\cdots 365}_{\text{10 times}}=365^{10}=4.2\cdot 10^{25}. \end{gathered} \] Let \(A\) be the event that at least two people have their birthday on the same day. What is \(A'\) then?

\(A'\) is the event that all 10 birthdays are different! The cardinality of \(A'\) is easy to find.

We form 10-item lists, where we have 365 possibilities for the first place, only 364 for the second place (since the birthdays must be different), and so on: \[ \begin{gathered} |A'|=365\cdot 364\cdot 363\cdots 356 = 3.7\cdot 10^{25}. \end{gathered} \] And thus we obtain: \[ \begin{gathered} P(A)=1-\frac{3.7\cdot 10^{25}}{4.2\cdot 10^{25}}\simeq 0.12\,. \end{gathered} \] This probability is surprisingly high. It becomes even clearer when we consider a group of 50 people. In this case, the probability that at least two people have their birthday on the same day is, \[ \begin{gathered} P(A)=1-\frac{3.9\cdot 10^{126}}{1.3\cdot 10^{128}}\simeq 0.97\,. \end{gathered} \] Thus, it is very likely that among 50 people, at least two will share the same birthday. Or in other words: it is very unlikely that all birthdays are different among 50 people. □

5.1.7 Discrete Distributions

All the random variables we have studied so far are discrete random variables. By this we mean that the set of their possible values is countable. Either this value set \(\mathcal S\) was finite, or it had no more elements than there are natural numbers.

In Exercise 5.16: \[ \begin{gathered} X\in\mathcal S_X,Y\in\mathcal S_Y,\quad \mathcal S_X,\mathcal S_Y=\{1,2,3,4,5,6\},\\ Z=X+Y\in \mathcal S_{Z}=\{2,3,4,\ldots,12\}. \end{gathered} \] In Exercise 5.17: \[ \begin{gathered} X\in\mathcal S_X,Y\in\mathcal S_Y,\quad \mathcal S_X,\mathcal S_Y=\{1,2,3,4,5,6\},\\ Z=X-Y\in\mathcal S_Z=\{-5,-4,-3,\ldots,3,4,5\}. \end{gathered} \] In Exercise 5.19: \[ \begin{gathered} S_{10}\in\mathcal S=\{0,1,2,\ldots,10\}. \end{gathered} \] In Exercise 5.20 the range was infinite for the first time: \[ \begin{gathered} W\in\mathcal S=\{1,2,3,\ldots\}=\mathbb N. \end{gathered} \] For all these and many other examples, it is easily possible to specify a function \(f_X(x)=P(X=x)\) for all values of \(x\in \mathcal S\). This function is called the probability function of the random variable \(X\). We can represent it by functional expressions or in the form of value tables.

For example Exercise 5.16, here \(Z=X+Y\): \[ \begin{gathered} f_X(x)=f_Y(x)=\frac{1}{6},\quad x=1,2,\ldots 6\\ \begin{array}{c|ccccccccccc} z & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12\\ \hline\\[-10pt] f_Z(z) & \frac{1}{36} &\frac{2}{36} & \frac{3}{36} & \frac{4}{36} & \frac{5}{36} & \frac{6}{36} & \frac{5}{36} & \frac{4}{36} & \frac{3}{36} & \frac{2}{36} & \frac{1}{36} \end{array}\ \end{gathered} \tag{5.6}\] Besides the probability function, we also need the concept of the distribution function \(F(x)\) of a random variable. It is defined by: \[ \begin{gathered} F(x)=P(X\le x)=\sum_{u\le x}f(u). \end{gathered} \tag{5.7}\] This is the cumulative sum of the values of the probability function. Unlike \(f(x)\), the distribution function \(F(x)\) is defined for all real numbers \(x\). It allows us to answer interesting questions directly.

Let’s take, for example, the random variable \(Z=X+Y\), whose probability function is given in (5.6). From it we calculate: \[ \begin{aligned} F_Z(2)&=P(Z\le 2)=P(Z=2)=\frac{1}{36}\\[4pt] F_Z(3)&=P(Z\le 3)= P(Z=2)+P(Z=3)=\frac{3}{36}\\[4pt] F_Z(4)&=P(Z\le 4)=P(Z=2)+\ldots+P(Z=4)=\frac{6}{36}\\[4pt] &\ldots\\ F_Z(12)&=P(Z\le 12)=P(Z=2)+\ldots+P(Z=12)=1\ \end{aligned} \tag{5.8}\] We can represent \(F_Z(z)\) more clearly in tabular form: \[ \begin{gathered} \begin{array}{c|ccccccccccc} z & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12\\ \hline\\[-10pt] f_Z(z) & \frac{1}{36} &\frac{2}{36} & \frac{3}{36} & \frac{4}{36} & \frac{5}{36} & \frac{6}{36} & \frac{5}{36} & \frac{4}{36} & \frac{3}{36} & \frac{2}{36} & \frac{1}{36} \\[4pt] F_Z(z) & \frac{1}{36} & \frac{3}{36} & \frac{6}{36} & \frac{10}{36} & \frac{15}{36} & \frac{21}{36} & \frac{26}{36} & \frac{30}{36} & \frac{33}{36} & \frac{35}{36} & 1 \end{array} \end{gathered} \] Now, we said earlier, the distribution function \(F(x)\) is defined for all real numbers. This property is not as clear in the tabular representation (5.8). In fact, the distribution function of a discrete random variable is a step function. Hence, (5.8) is actually as follows (values as rounded floating-point numbers): \[ \begin{gathered} F_Z(z)=P(Z\le z)=\left\{\begin{array}{cl} 0.000 & \text{for } z<2\\[4pt] 0.028 & 2\le z < 3\\[4pt] 0.083 & 3\le z < 4\\[4pt] 0.167 & 4\le z < 5\\[4pt] 0.278 & 5\le z < 6\\ \vdots &\\ 0.972 & 11\le z < 12\\[4pt] 1.000 & z\ge 12 \end{array} \right. \end{gathered} \tag{5.9}\] This function is illustrated in Figure 5.4.

Figure 5.4: The distribution function \(F_Z(z)\) corresponding to (5.9).

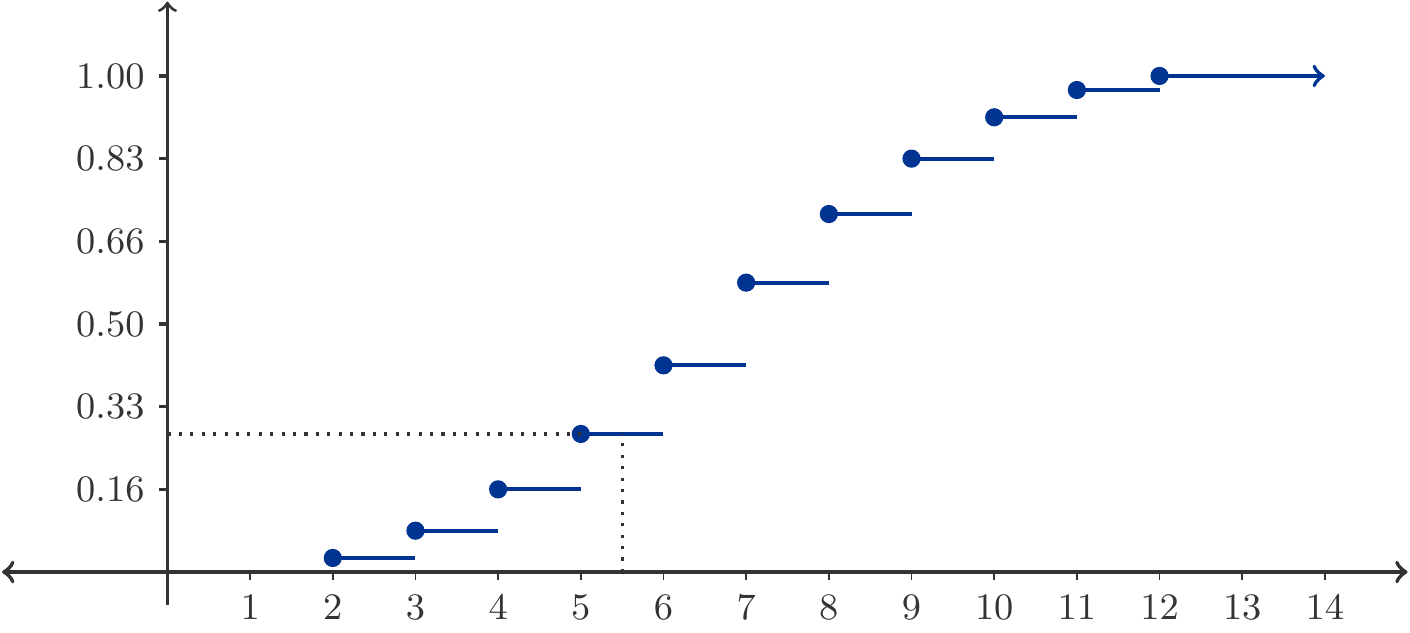
This figure shows us that a discrete distribution function exhibits jumps at those points \(x\) for which \(f(x)>0\). Between the jumps, the distribution function is constant.

For example, we can read: \[ \begin{gathered} F_Z(5.5)=P(Z\le 5.5)=P(Z\le 5)=\frac{10}{36}\approx 0.278 \end{gathered} \] The distribution function condenses important information: \[ \begin{aligned} %% {alignat*}{2} P(X>a)&=1-P(X\le a)&=&\;1-F(a),\\[4pt] P(a<X\le b)&=P(X\le b)-P(X\le a)&=&\;F(b)-F(a). \end{aligned} \] These properties also hold under much more general conditions, so we summarize in the form of a theorem:

Theorem 5.22 (Characteristic of the Distribution Function)  

• The distribution function \(F(x)\) is defined for all real numbers.

• \(0\le F(x)\le 1\).

• \(F(x)\) is monotonic increasing.

• \(\lim_{x\to-\infty}F(x)=0\), \(\lim_{x\to\infty}F(x)=1\).

• \(P(X\le a)=F(a)\).

• \(P(X>a)=1-F(a)\).

• \(P(a<X\le b)=F(b)-F(a)\).

Exercise 5.23 Let \(N\) be the number of machine failures per day in an offset printing company. The probability function of \(N\) has been estimated from past collected data: \[ \begin{gathered} \begin{array}{c|cccccc} n & 0 & 1 & 2 & 3 & 4 & 5\\ \hline\\[-10pt] P(N=n) & 0.224 & 0.336 & 0.252 & 0.126 & 0.047 & 0.015 \end{array} \end{gathered} \] More than 5 failures per day have never been observed.

Determine the distribution function of \(N\).

What is the probability of more than 3 failures per day?

Solution: The cumulative distribution function \(F(n)=P(N\le n)\) is obtained from the cumulative values of the probability function: \[ \begin{gathered} \begin{array}{c|cccccc} n & 0 & 1 & 2 & 3 & 4 & 5\\ \hline\\[-10pt] P(N=n) & 0.224 & 0.336 & 0.252 & 0.126 & 0.047 & 0.015\\[3pt] P(N\le n)& 0.224 & 0.560 & 0.812 & 0.938 & 0.985 & 1.000 \end{array} \end{gathered} \] The probability of observing more than 3 failures in one day is: \[ \begin{gathered} P(N>3)=1-P(N\le 3)=1-0.938 = 0.062\,. \end{gathered} \] □

5.1.8 Continuous Distributions

Discrete random variables take on values in a finite or countably infinite set. They often express count results, such as the number of games won, the number of customers waiting in line at an airport check-in counter, the number of machine failures per day, the number of children per family, etc.

There is also another class of random variables that assume values in an interval. They typically arise not through counting, but through measurements that result in very specific measured values. Here are some examples:

• Waiting times for customers, service life of products, etc.
• Distances, lengths, weights, etc.
• Returns on financial investments
  and much more.

The value \(P(t)\) of a portfolio at time \(t\) is expressed in units of currency and is strictly speaking a discrete quantity. However, since the range of values for \(P(t)\) is usually very large relative to the smallest currency unit (e.g., one Euro cent), \(P(t)\) will be approximately treated as a continuous quantity.

Events that we express using continuous random variables are no longer point events, like \(\{X=5\}\), but intervals on the number line.

To assign probabilities to such intervals, we need the concept of a density function.

The density of a continuous random variable \(X\) is a continuous function \(f(x)\) with \[ \begin{gathered} f(x)\ge 0,\qquad \int_{-\infty}^\infty f(x)\,\mathrm{d}x = 1. \end{gathered} \] The last requirement states (see Chapter 4) that the area under the density must be equal to 1. In fact, it is areas under \(f(x)\) that represent probabilities. In particular, we have: \[ \begin{gathered} F(a)=P(X\le a)=\int_{-\infty}^af(x)\,\mathrm{d}x. \end{gathered} \] The function \(F(x)\) is called the distribution function of \(X\), just as in the case of discrete random variables. It possesses all the properties formulated in Theorem 5.22. In particular, we have: \[ \begin{aligned} P(X>a)&=\int_a^\infty f(x)\,\mathrm{d}x=1-F(a),\\[5pt] P(a<X\le b)&= \int_a^bf(x)\,\mathrm{d}x=F(b)-F(a). \end{aligned} \] Figure 5.5 illustrates these relationships.

Figure 5.5: Density and probabilities.

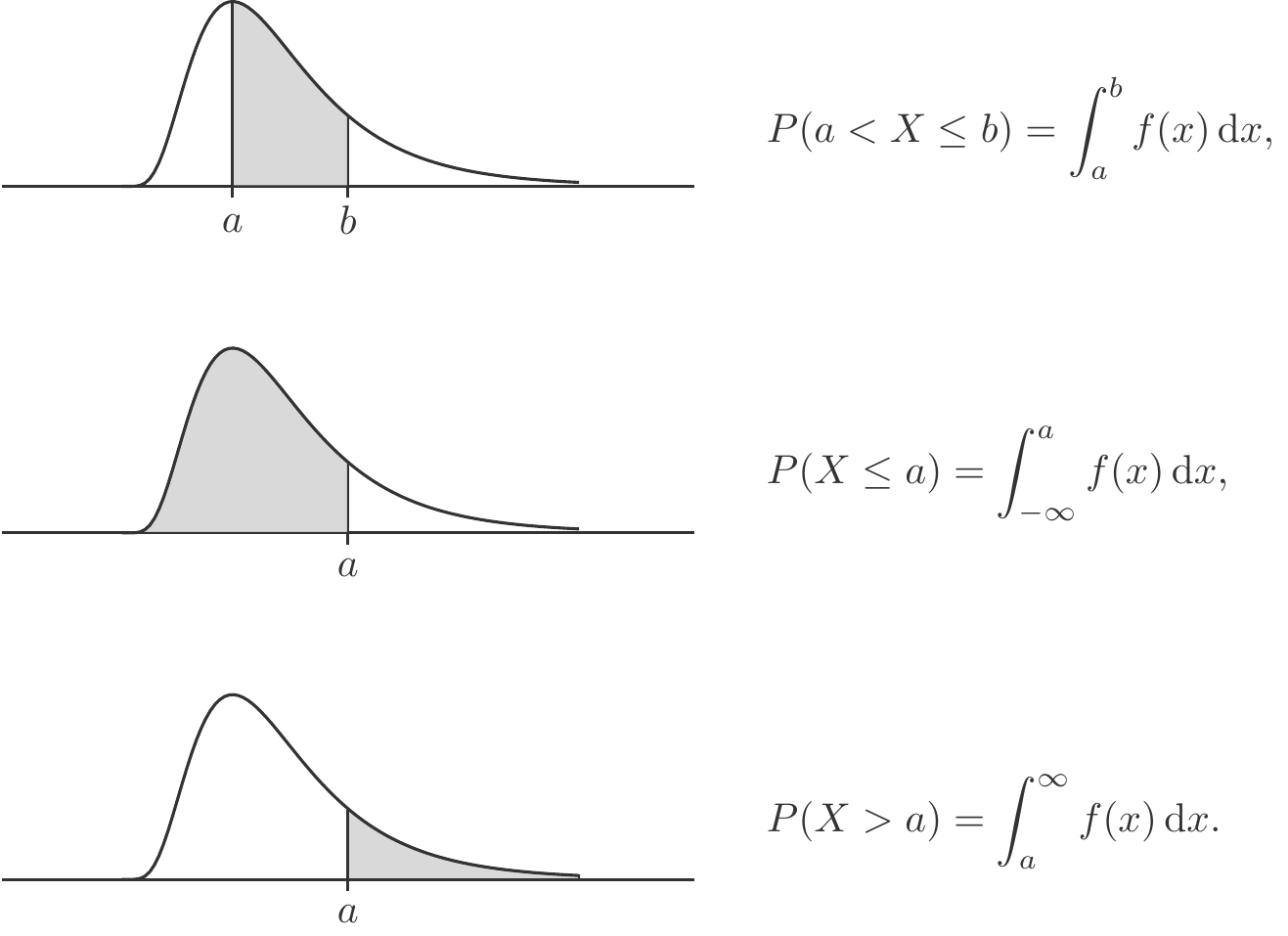
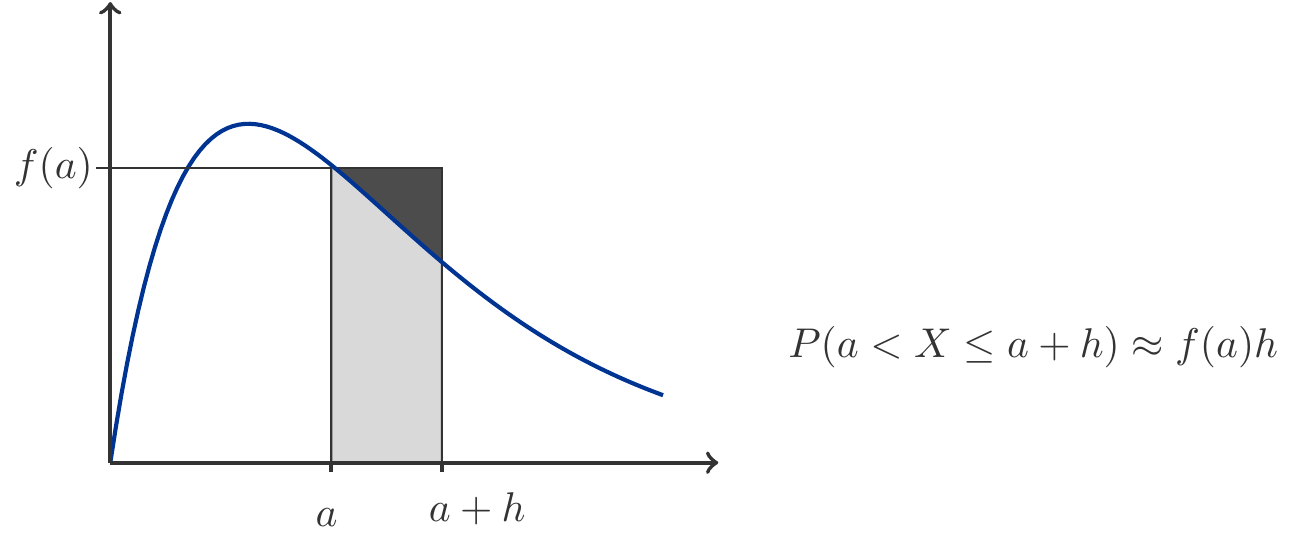
Furthermore, the cumulative distribution function of a continuous random variable is differentiable at all points where the density \(f(x)\) is continuous, and it holds that: \[ \begin{gathered} f(x)=F'(x). \end{gathered} \tag{5.10}\] It is important to emphasize that the function values of the density function \(f(x)\) are not probabilities. However, for very small values of \(h>0\) (principle of local linearization, Chapter 3, see also Figure 5.6), it approximately holds that: \[ \begin{gathered} P(x< X\le x+h)\approx f(x) h. \end{gathered} \tag{5.11}\]

Figure 5.6: Illustration of the principle of local linearization.

This has another important consequence that gives rise to another characteristic property of continuous random variables. When we let \(h\to 0\) and if \(a\) is not a discontinuity point (jump point) of the density, then \[ \begin{gathered} \lim_{h\to 0} P(a<X\le a+h)=P(X=a)=0. \end{gathered} \tag{5.12}\] This property is very peculiar, yet typical for continuous random variables. Although we have demanded in Theorem 5.9 that the impossible event be assigned probability zero, it is clear that the converse of this statement is not correct. Boris Gnedenko (1912–1995), an eminent Russian probabilist, tried to explain this fact to his students as follows: we must distinguish between the theoretical impossibility of an event (e.g., rolling a 7 with a 6-sided die), and practical impossibility. Let’s assume that \(X\) is the lifespan of an energy-saving light bulb. Obviously, \(X\) takes its values in the interval \([0,\infty)\). It is theoretically possible that \(X\) lasts 1000 hours. But in practice, this is impossible, hence \(P(X=1000)=0\).

An intuitive argument that supports the formal aspect (5.12) would be this: The statement \(\{X=1000\}\) implies, among other things, that the value of the random variable is not 1000.00000000001 nor 999.999999999999. So, if we make a bet on the event \(\{X=1000\}\), then we would lose this bet if the value of the random variable \(X\) differs by an extremely small, practically immeasurable amount from 1000. Since this will almost always be the case, we will always lose the bet. This is precisely what the equation \(P(X=1000)=0\) means.

Example 5.24 (Exponential Distribution)

The Exponential Distribution is one of the most important continuous distributions. We say that a random variable \(T\) is exponentially distributed, when its density is given by: \[ \begin{gathered} f(t)=\left\{\begin{array}{cl} 0 & t<0\\ \lambda e^{-\lambda t} & t\ge 0 \end{array}\right.,\qquad \lambda >0 \end{gathered} \tag{5.13}\] The parameter \(\lambda\) is called the event rate, and this term also hints at the most important applications of the Exponential Distribution. It is commonly used to model time intervals \(T\) between random events. These events can be:

• Arrivals of customers in the broadest sense, e.g., passengers at an airport, customers in a bank;

• Failures of technical equipment: The time between two failures of a machine, its up-time, is often exponentially distributed.

• The time intervals between emissions of \(\alpha\)-particles by a nucleus: this was even the original application of the Exponential Distribution in the early 20th century.

The distribution function is easily determined using the methods that we learned in Chapter 4: \[ \begin{gathered} P(T\le t)=F(t)=\int_0^t\lambda e^{-\lambda s}\,\mathrm{d}s=-e^{-\lambda s}\bigg|_0^t=1-e^{-\lambda t},\qquad t\ge 0. \end{gathered} \] The density possesses a discontinuity (jump) at \(t=0\). The distribution function has a corner at this point and is not differentiable there. However, for all \(t>0\) we have \(F'(t)=f(t)\), as the reader should verify.

The event rate \(\lambda\) is to be interpreted as follows: its value tells us, how closely events follow each other. The larger \(\lambda\), the smaller is the average distance between events, the more closely they follow one another. The smaller \(\lambda\), the less densely the events follow each other, their average distances are correspondingly larger.

Figure 5.7: Density \(f(t)\) and distribution \(F(t)\) of an Exponential Distribution with \(\lambda =1\).

Exercise 5.25 (Hospital Management) Studies in the United States have shown that the length of stay (in days) of patients in intensive care units (ICUs) can be very well approximated by an exponential distribution with \(\lambda=0.2564\). This corresponds to an average length of stay of 3.9 days.

1. What percentage of patients have to spend more than 10 days in an ICU?

2. What critical length of stay is exceeded by 1% of the patients?

Solution:
(a) Let \(T\) be the length of stay. \[ \begin{aligned} P(T>10)&=1 - P(T\le 10)\\ &=1 -(1-e^{-10\cdot 0.2564})=e^{-2.564}= 0.076996 \approx 0.077\,. \end{aligned} \] About 7.7% of patients stay longer than 10 days in the ICU.

(b) We are looking for a time span \(t\) such that \(P(T>t)=0.01\): \[ \begin{gathered} P(T>t)=e^{-0.2564 t}=0.01\\ \implies t=-\frac{\ln(0.01)}{0.2564} =17.961 \approx 18\text{ days}. \end{gathered} \] □

Example 5.26 (Logistic Distribution)

A random variable \(X\) is called logistically distributed if it has the following distribution function and density: \[ \begin{aligned} F(x)&=P(X\le x)=\frac{1}{1+e^{-(x-\mu)/s}},\qquad x\in\mathbb R\\[5pt] f(x)&=\frac{e^{-(x-\mu)/s}}{s\left(1+e^{-(x-\mu)/s}\right)^2}\,.\ \end{aligned} \tag{5.14}\] The parameter \(\mu\) is (see Section 5.3.1) and indicates the location of the maximum of the density \(f(x)\), \(s\) is a scale parameter. The applications of the Logistic Distribution are diverse, ranging from statistical data analysis through technical reliability to financial mathematics. For instance, there are sound (statistical) reasons to use the Logistic Distribution for modeling returns of financial assets.

Figure 5.8: Density \(f(x)\) and distribution function \(F(x)\) of a logistic distribution with \(\mu =2\) and \(s=1\).

Exercise 5.27 (Financial Mathematics) The annual return \(X\) of a security is logistically distributed with \[ \begin{gathered} P(X\le x)=\frac{1}{1+e^{-(x-0.1)/0.022}}. \end{gathered} \] At the beginning of a year, 2000 Units of currency (GE) were invested in the security.

1. What is the probability that the profit at the end of the year exceeds 300 units of currency (GE)?

2. What is the probability that the return is negative, thus resulting in a loss of capital?

Solution: (a) Since the profit \(G=2000X\), we have: \[ \begin{gathered} G>300\Leftrightarrow 2000X>300 \implies X>\frac{300}{2000}=0.15\,. \end{gathered} \] Therefore: \[ \begin{aligned} P(X>0.15) & = 1-P(X\le 0.15) \\ & = 1-\frac{1}{1+e^{-(0.15-0.1)/0.022}}=0.093407\,. \end{aligned} \] The probability of this occurring is thus approximately 9.3%.

(b) We are looking for \(P(X\le 0)\): \[ \begin{gathered} P(X\le 0)=\frac{1}{1+e^{-(0-0.1)/0.022}}=0.010504. \end{gathered} \] This undesirable scenario therefore occurs with a probability of about 1%. □

5.2 Conditional Probabilities

5.2.1 Fourfold Tables

Let \(A\) and \(B\) be two events associated with a random experiment. We can also imagine these as two subsets within a finite population.

We conduct the random experiment (for example, drawing an element from the population) and record which of the two events occur. We compile the possible combinations of events in a table: \[ \begin{gathered} \begin{array}{c|cc} & B & B' \\ \hline A & A\cap B & A\cap B' \\ A' & A'\cap B & A'\cap B'\\ \end{array} \end{gathered} \] Here, \(A'\) denotes the complementary event of \(A\), as usual.

If we populate this table with the respective probabilities, we obtain a fourfold table or contingency table. We can add the probabilities of the individual events at the margins of the table, which can be calculated as row or column totals according to the addition rule. \[ \begin{gathered} \begin{array}{c|cc|c} & B & B' &\\ \hline A & P(A\cap B) & P(A\cap B') & P(A) \\ A' & P(A'\cap B) & P(A'\cap B') & P(A')\\ \hline & P(B) & P(B') & 1 \end{array} \end{gathered} \] The probabilities that come out as row and column totals, namely \(P(A), P(A'), P(B)\) and \(P(B')\), are called total probabilities. Thus, \[ \begin{gathered} P(A)=P(A\cap B) + P(A\cap B') \end{gathered} \] is the total probability of the event \(A\). This means the probability of \(A\) occurring, regardless of whether it occurred with \(B\) or its complement. Obviously, the fundamental addition rule (5.2) is behind this, because the events \(\{A\cap B\}\) and \(\{A\cap B'\}\) are certainly mutually exclusive: \[ \begin{gathered} (A\cap B)\cap (A\cap B')=A\cap B\cap B'=\varnothing, \end{gathered} \] since \(B\cap B'=\varnothing\). The total probabilities for \(A', B\) and \(B'\) are calculated analogously.

To completely fill out a fourfold table, one only needs three independent pieces of information.

Example 5.28 (The ELISA Test)

ELISA (Enzyme-linked Immunosorbent Assay) is a method available since the mid-1980s for detecting antibodies against the HIV virus in human blood. It is a relatively low-cost test that is used to screen blood banks, but also to test groups of people, such as military recruits, for HIV. ELISA is a screening test, meaning it is primarily used to identify all people in a group, or their blood donations, who may be infected with HIV.

For this example, we define the following two events: \[ \begin{aligned} A &= \text{\{a person is infected with the HIV virus}\\ &\phantom{=\{} \text{and has formed antibodies against the virus\}},\\[5pt] B &=\text{\{ELISA yields a positive test result\}}. \end{aligned} \] In a large-scale study (> 50000 participants), the following probabilities were estimated: \[ \begin{gathered} \begin{array}{l|cc|r} & B & B' &\\ \hline A & 0.0038 & 0.0002 & 0.0040\\ A'& 0.0301 & 0.9659 & 0.9960\\ \hline & 0.0339 & 0.9661 & 1.0000 \end{array} \end{gathered} \] What do these data tell us?

• The proportion of HIV-infected people in the total population, the prevalence of HIV, is \(P(A)=0.004\), or 0.4%.

• The proportion of participants who tested positive is \(P(B)=0.0339\).

• With a probability of \(P(A\cap B')=0.0002\), a participant was infected with HIV and had a negative test result.

• With probability \(P(A'\cap B)=0.0301\), a participant was not infected and yet had a positive test result.

These are insights that can be directly read from the contingency table.

But there is more information contained within this table.

Definition 5.29 (Conditional Probability) Let \(A\) and \(B\) be events with \(P(B)>0\), then \[ \begin{gathered} P(A|B)=\frac{P(A\cap B)}{P(B)} \end{gathered} \tag{5.15}\] is the conditional probability of the event \(A\) given the condition \(B\).

This definition answers the question: Among how many cases in which event \(B\) occurs, does the event \(A\) also occur?

The formula (5.15) is easy to understand when interpreted as a statement about proportions in finite populations: The conditional probability is identical to the proportion of \(A\) in the entirety of \(B\).

We continue with Example 5.28.

Example 5.30 (Continuation of Example 5.30)

We first calculate \(P(A|B)\). This is the probability that someone who tested positive using ELISA (event \(B\)) is actually a carrier of the HIV virus (event \(A\)). With (5.15) we obtain: \[ \begin{gathered} P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{0.0038}{0.0339} = 0.1121\,. \end{gathered} \] This is interesting: someone who tested positive is actually infected with the HIV virus with a probability of only about 11%.

Now we calculate \(P(B|A)\), which is the proportion of those who tested positive (event \(B\)) among the HIV-infected (event \(A\)): \[ \begin{gathered} P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{0.0038}{0.0040} = 0.95\,. \end{gathered} \] This probability is called sensitivity of the test in a medical context. Naturally, one would like this probability to be as high as possible, because this is the probability that a person infected with HIV will actually be detected by ELISA.

Another interesting value is \(P(B'|A')\): \[ \begin{gathered} P(B'|A') = \frac{P(A' \cap B')}{P(A')} = \frac{0.9659}{0.9960} = 0.9698\,. \end{gathered} \] This is the probability that someone who is not HIV infected will have a negative test result, the specificity of ELISA. Here too, it is clear that one would like to achieve the highest possible values for this probability. The specificity of ELISA is about 97% here.

And finally \(P(A'|B')\). How certain can someone who tested negative be that they are not infected with HIV? \[ \begin{gathered} P(A'|B') = \frac{P(A' \cap B')}{P(B')} = \frac{0.9659}{0.9661} = 0.9998\,. \end{gathered} \] This value is reassuring.

From the definition of conditional probability (Definition 5.29), an important formula follows. It allows us to express the probability that two events occur together, using conditional probability:

Theorem 5.31 (Product Rule) The product rule applies: \[ \begin{gathered} P(A \cap B) = P(A|B)P(B). \end{gathered} \tag{5.16}\] This formula is also called the multiplication theorem.

In some problems, the conditional probabilities are known, but other probabilities are missing. In such cases, the missing probabilities must be calculated from the conditional probabilities. For this purpose, we use the product rule (5.16).

Exercise 5.32 (The typical women’s car is small and pink) In a study conducted in Germany in 2013, behavioral differences between men and women when purchasing a new car were examined. In the year 2013, 24% of the new cars were purchased by women, and 76% by men. Company cars were not included in the survey.

The focus of the investigation was, among other things, the widespread prejudice that women prefer small cars. For this purpose, the cars were divided into small cars \(K\) and non-small cars \(K'\) (sedans, station wagons, SUVs, etc.).

It was found that a full 10% of men could see themselves purchasing a small car, while it was 28% for women.

1. What percentage of the sold cars are small cars?

2. What percentage of the small car buyers are male?

Solution: First, we define the events of interest: \[ \begin{aligned} K & =\{\text{a compact car is purchased}\},\\ F & =\{\text{buyer is female}\},\\ M & =\{\text{buyer is male}\}. \end{aligned} \] The information tells us that 10% of compact car buyers are male, while the percentage for women is 28%. Therefore, we know two conditional probabilities: \[ \begin{gathered} P(K|M)=0.1,\quad P(K|F)=0.28\,. \end{gathered} \] Moreover, we know: \[ \begin{gathered} P(F)=0.24,\quad P(M)=1-P(F)=0.76. \end{gathered} \] Using the product formula (5.16), we can now calculate: \[ \begin{aligned} P(K\cap M)&= P(K|M)P(M)=0.1\cdot 0.76=0.076,\\ P(K\cap F)&= P(K|F)P(F)=0.28\cdot 0.24=0.0672\,. \end{aligned} \] With this, we have the groundwork for a contingency table: \[ \begin{gathered} \begin{array}{l|cc|c} &M & F\\ \hline K & 0.0760 & 0.0672 &\\ K'& & &\\ \hline & 0.7600 & 0.2400 & 1.0000 \end{array} \end{gathered} \] The missing values can easily be found by completing the rows and columns, so that we finally have the following complete contingency table: \[ \begin{gathered} \begin{array}{l|cc|c} &M & F\\ \hline K & 0.0760 & 0.0672 & 0.1432\\ K'& 0.6840 & 0.1728 & 0.8568\\ \hline & 0.7600 & 0.2400 & 1.0000 \end{array} \end{gathered} \] Now we can answer the posed questions.

The market share of compact cars is 14.3%, because \(P(K)=0.1432\).

The proportion of male buyers among compact car buyers is: \[ \begin{gathered} P(M|K)=\frac{P(M\cap K)}{P(K)}=\frac{0.0760}{0.1432}=0.5307\,. \end{gathered} \] Indeed, 53% of compact cars are bought by men! As for how many of them are pink, the data does not tell us. □

5.2.2 Independent Events

It is possible for two events \(A\) and \(B\) to satisfy the relationship \[ \begin{gathered} P(A|B)>P(A) \end{gathered} \] In this case, one could say that the event \(B\) favors the occurrence of \(A\). However, this formulation can be misleading as it suggests a causal effect of \(B\) on \(A\). In reality, the inequality is completely symmetrical in \(A\) and \(B\), as can be seen from \[ \begin{gathered} P(A|B)>P(A) \Leftrightarrow P(A\cap B)>P(A)P(B) \Leftrightarrow P(B|A)>P(B) \end{gathered} \] It is therefore more accurate to say that in this case the two events \(A\) and \(B\) favor each other or are positively coupled.

Similarly, in the case of \[ \begin{gathered} P(A|B)<P(A) \Leftrightarrow P(A\cap B)<P(A)P(B) \Leftrightarrow P(B|A)<P(B), \end{gathered} \] it is said that the two events hinder each other or are negatively coupled.

Exercise 5.33 (Accident Statistics) Out of 1000 traffic accidents, 280 had a fatal outcome (event \(A\)) and 100 occurred at a speed of over 150 km/h (event \(B\)). 20 accidents were non-fatal and occurred at speeds above 150 km/h.

1. What is the probability that a high-speed accident is fatal?

2. What is the probability that a fatal accident occurred at high speed?

3. Assess the coupling of events \(A\) and \(B\). Try to interpret the coupling causally.

Solution: The absolute frequencies are: \[ \begin{gathered} \begin{array}{c|cc|c} & B & B' &\\ \hline A & & & 280\\ A'&20 & & \\ \hline & 100 & & 1000 \end{array} \quad\Rightarrow\quad \begin{array}{c|cc|c} & B & B' &\\ \hline A & 80&200 & 280\\ A'& 20 &700& 720 \\ \hline & 100 &900 &1000 \end{array} \end{gathered} \] The estimated probabilities are then \[ \begin{gathered} \begin{array}{c|cc|c} & B & B' &\\ \hline A & 0.08& 0.20 & 0.28\\ A'&0.02 & 0.70& 0.72 \\ \hline & 0.10 & 0.90 &1.00 \end{array} \end{gathered} \] (a) The proportion of fatal traffic accidents to high-speed accidents is: \[ \begin{gathered} P(A|B)=\dfrac{P(A\cap B)}{P(B)}=\dfrac{0.08}{0.1}=0.8\,. \end{gathered} \] (b) The proportion of high-speed accidents to traffic accidents with fatalities is: \[ \begin{gathered} P(B|A)=\dfrac{P(A\cap B)}{P(A)}=\dfrac{0.08}{0.28}=0.2857\,. \end{gathered} \] (c) Since \(P(A|B)>P(A)=0.28\) and \(P(B|A)>P(B)=0.1\), there is a positive coupling. The two events favor each other.

These results suggest that high speed might be a cause for the fatal outcome of an accident. However, this conclusion is not compelling. It could also be that certain character traits of the driver cause both the high speed and the fatality of the accident. □

It is important to always remember that coupling of two events does not have to be an indication of a causal relationship between the events. It is very common for stratification of the population to be the cause of a spurious coupling of events.

No coupling occurs when \(P(A|B)=P(A)\) or \(P(B|A)=P(B)\). In this case, the two events are called independent. This has an important consequence: \[ \begin{aligned} P(A|B)=P(A) & \implies \frac{P(A \cap B)}{P(B)}=P(A) \\ & \implies P(A \cap B)=P(A)P(B). \end{aligned} \]

Theorem 5.34 (Stochastic Independence) Two events \(A\) and \(B\) are stochastically independent if \[ \begin{gathered} P(A\cap B)=P(A)P(B). \end{gathered} \tag{5.17}\] Otherwise, they are stochastically dependent or coupled.

When dealing with more than two events \(A_1,A_2,\ldots,A_n\), independence means that for all selections \(i_1<i_2<\ldots< i_k\) the equation \[ \begin{gathered} P(A_{i_1}\cap A_{i_2}\cap\ldots\cap A_{i_k})= P(A_{i_1})P(A_{i_2})\cdots P(A_{i_k}) \end{gathered} \tag{5.18}\] is true.

There are numerous cases of application where one knows in advance that certain events are independent. This information can then be used to determine probabilities. Indeed, many problems are significantly simplified by assuming independence.

Exercise 5.35 (Process Engineering) A technical system consists of three parts, which can fail independently of each other. The failure probabilities of the individual parts are 0.2, 0.3, and 0.1. Let \(X\) denote the number of failing parts. Determine the probability function of the random variable \(X\), i.e. \[ \begin{gathered} P(X=0),\quad P(X=1), \quad P(X=2),\quad P(X=3). \end{gathered} \]

Solution: Let \(A,\,B,\, C\) denote the events that each of the three parts fails, respectively. Given are the probabilities \(P(A)=0.2\), \(P(B)=0.3\) and \(P(C)=0.1\).

Taking into account the independence of the events \(A,B,C\) and using the addition rule, we obtain: \[ \begin{gathered} \small \begin{array}{l l } P(X=0) & = P(A'\cap B'\cap C')=P(A')P(B')P(C')\\[4pt] & = 0.8 \cdot 0.7 \cdot 0.9 = 0.504,\\[7pt] P(X=1) & = P(A\cap B' \cap C')+ P(A'\cap B \cap C')+ P(A'\cap B' \cap C)\\[4pt] & = P(A)P(B')P(C')+P(A')P(B)P(C')+P(A')P(B')P(C)\\[4pt] & =0.2\cdot 0.7 \cdot 0.9 + 0.8\cdot 0.3 \cdot 0.9 + 0.8\cdot 0.7\cdot 0.1 = 0.398,\\[7pt] P(X=2) & = P(A\cap B\cap C')+ P(A\cap B'\cap C)+ P(A'\cap B \cap C)\\[4pt] & = P(A)P(B)P(C')+P(A)P(B')P(C)+P(A')P(B)P(C)\\[4pt] & = 0.2\cdot 0.3 \cdot 0.9 + 0.2 \cdot 0.7 \cdot 0.1 + 0.8 \cdot 0.3 \cdot 0.1 =0.092,\\[7pt] P(X=3) & = P(A \cap B\cap C)=P(A)P(B)P(C)\\[4pt] &= 0.2 \cdot 0.3 \cdot 0.1 = 0.006\,. \end{array} \end{gathered} \]

Thus, the probability function of the random variable \(X\) in tabular form is: \[ \begin{gathered} \begin{array}{c|cccc} k & 0 & 1 & 2 & 3\\ \hline P(X=k) & 0.504 & 0.398 & 0.092 & 0.006 \end{array} \end{gathered} \] □

The concept of independence can also be applied to random variables, because statements about random variables such as \(\{X>b\}\) or \(\{a<X≤b\}\) are random events.

Definition 5.36 Two random variables \(X\) and \(Y\) are called stochastically independent if statements about the random variables are stochastically independent events.

Remark 5.37 If \(X\) and \(Y\) are independent, then the events \(\{X\le a\}\) and \(\{Y\le b\}\) are also independent. Therefore, \[ \begin{gathered} P(\{X\le a\}\cap \{Y\le b\})=P(X\le a)\cdot P(Y\le b). \end{gathered} \] Since expressions like the one on the left side of this equation occur frequently in applications (e.g., in statistics), a simplified comma notation has become customary: \[ \begin{gathered} P(\{X\le a\}\cap \{Y\le b\})=P(X\le a, Y\le b). \end{gathered} \]

Exercise 5.38 (A Call Center) A company operates a call center to efficiently process customer inquiries. It is known that the duration \(T\) (in minutes) of a customer call is a continuous random variable with distribution function \(P(T\le t)=1-e^{-t/10}\).

Three customers call at the same time and are immediately connected to an agent. Their calls last \(T_1, T_2\), and \(T_3\) minutes, where these random variables are stochastically independent.

What is the probability that the longest of the three calls lasts longer than 20 minutes?

Solution: Let \(M=\max(T_1,T_2,T_3)\), where \(T_1,T_2\), and \(T_3\) are independent. We first consider the event \(\{M\le h\}\). This event can only occur if every \(T_i\le h\): \[ \begin{gathered} \{M\le h\} \Leftrightarrow \{T_1\le h\}\cap \{T_2\le h\} \cap \{T_3\le h\}, \end{gathered} \] because if just one \(T_i>h\), then \(M\) could no longer be \(\le h\). Equivalent events have the same probability, therefore: \[ \begin{aligned} P(M\le h)&=P(T_1\le h,T_2\le h,T_3\le h)\\[4pt] &=P(T_1\le h)\cdot P(T_2\le h)\cdot P(T_3\le h)\quad\text{(Independence)}\\[4pt] &=(1-e^{-h/10})^3. \end{aligned} \] We are looking for \[ \begin{aligned} P(M>20)&=1-P(M\le 20)=1-(1-e^{-20/10})^3=0.3535. \end{aligned} \] This is a relatively high probability, because one conversation, say the first one, lasting longer than 20 minutes is only: \[ \begin{gathered} P(T_1>20)=e^{-20/10}=0.1353. \end{gathered} \] □

5.3 Expected Value and Variance

5.3.1 The Concept of Expected Value

Let \(X\) be a random variable. If the underlying random experiment is repeated frequently and the resulting values of the random variable \(X\) are collected, then a data list \(x_1,x_2,\ldots\) is created. We can now calculate the averages \[ \begin{aligned} \bar{x}_1 &=\frac{x_1}{1},\;\bar{x}_2=\frac{x_1+x_2}{2},\;\bar{x}_3=\frac{x_1+x_2+x_3}{3}, \\ \bar{x}_4 &=\frac{x_1+x_2+x_3+x_4}{4}, \ldots \end{aligned} \tag{5.19}\] and study the progression of the averages with an increasing number of data. With many random variables, it is observed that these averages tend to approach a fixed value over time (provided that the repetitions are independent and occur under identical conditions). This limit is the long-term average of the random values of the random variable and is referred to as the expected value of the random variable.

Remark 5.39 (Existence of Expected Values) It is by no means the case that for every random variable the averages of the data lists converge. If that is not the case, then the concept of the expected value does not make sense for such a random variable. In that case, one says that the random variable does not possess an expected value. However, we will not consider such random variables in the following.

Figure 5.9: The averages (5.19) from 200 dice rolls.

Our explanation of the term expected value is quite similar to our explanation of the concept of probability. This also results in a first fundamental relationship between probabilities and expected values.

Let \(A\) be an event, and let \(X_A\) be the following random variable: \[ \begin{gathered} X_A(\omega)=\left\{\begin{array}{ll} 1 &\text{if $\omega\in A$},\\ 0 &\text{if $\omega\not\in A$} \end{array}\right. \end{gathered} \] The random variable \(X_A\) indicates the occurrence of the event \(A\). That’s why it is called the indicator variable of the event \(A\).

To determine the expected value of an indicator variable \(X_A\), one must look at the averages of data lists that are generated by an indicator variable. It is easy to see that these averages are identical to the relative frequencies with which the event \(A\) occurs in a series of repetitions of the random experiment. Therefore, the limit of the averages of \(X_A\) must coincide with the limit of the relative frequencies of \(A\). This means \(E(X_A)=P(A)\).

Another fundamental property of the expected value of random variables is a rule called linearity.

If \(X\) and \(Y\) are two random variables and \(a,b\in\mathbb R\) are any real numbers. Then we can form another random variable \(Z=aX+bY\). It’s obvious that for the averages \(\overline{x}, \overline{y}\), and \(\overline{z}\) of data lists of these random variables the equation \(\overline{z}=a\overline{x}+b\overline{y}\) holds. This implies \(E(Z)=aE(X)+bE(Y)\).

In a very similar way, it is reasoned that a random variable whose values are nonnegative must also have a nonnegative expected value: \(X\ge 0 \implies E(X)\ge 0\).

To summarize:

Theorem 5.40 The expected value of random variables has the following properties:

(a) The expected value of an indicator variable is identical to the probability of the underlying event: \[ \begin{gathered} E(X_A)=P(A). \end{gathered} \]

(b) The expected value of a linear combination of random variables is identical to the corresponding linear combination of the expected values: \[ \begin{gathered} E(aX+bY)=aE(X)+bE(Y). \end{gathered} \]

(c) The expected value of a nonnegative random variable is nonnegative: \[ \begin{gathered} X\ge 0 \implies E(X)\ge 0. \end{gathered} \]

Exercise 5.41 (Cost model) A manufacturing company operates with monthly fixed costs of 1000 CU and variable costs of 5 CU per piece. The monthly production is a random variable with an expected value of 300 pieces. Find the expected value of the monthly costs.

Solution: Let \(X\) represent the monthly production and \(Y\) the monthly costs, so \(Y=1000+5X\). Consequently, we have \[ \begin{gathered} E(Y)=E(1000+5X)=1000+5E(X)=1000+5\cdot 300=2500. \end{gathered} \] □

5.3.2 Calculation of Expectation Values

In the following examples, we calculate expectation values of random variables that can take on finitely many different values.

Let \(X\) be, for example, a random variable with two possible values \(a\) and \(b\) and let \(A=\{X=a\}\) and \(B=\{X=b\}\). Then the random variable \(X\) can be represented as a linear combination of indicator variables: \[ \begin{gathered} X=aX_A+bX_B. \end{gathered} \] It is very important to fully understand the validity of this equation: If \(\{X=a\}\) is true, then \(X_A=1\) and \(X_B=0\). Accordingly, the linear combination on the right-hand side has the value \(a\), and the equation is correct. The same applies if \(\{X=b\}\) is true.

From the validity of the equation \(X=aX_A+bX_B\), it follows from the rules for calculating expectation values that \[ \begin{gathered} E(X)=aE(X_A)+bE(X_B)=aP(A)+bP(B). \end{gathered} \] This observation can be generalized to random variables that can take on finitely many values.

Theorem 5.42 Let \(X\) be a random variable that takes on values \(a_1, a_2,\ldots,a_n\) with probabilities \(P(X=a_k)=p_k\). Then \(E(X)\) is: \[ \begin{gathered} E(X)=a_1p_1+a_2p_2+\cdots+a_np_n. \end{gathered} \tag{5.20}\] In other words: \(E(X)\) is a weighted average of the values \(a_1,\ldots,a_n\) of \(X\), weighted with the probabilities \(p_1,\ldots,p_n\).

Exercise 5.43 (Dice Roll) (a) What is the expected number of dots when rolling a die?

(b) Find the expected value of the sum of the dots when rolling a die twice.

Solution: The number of dots is a random variable \(X\) with values \(1,2,\ldots,6\), each with a probability of \(1/6\).

(a) We apply (5.20): \[ \begin{aligned} E(X)&=1\cdot P(X=1)+2\cdot P(X=2)+\cdots+6\cdot P(X=6)\\ &=\frac{1}{6}(1+2+\cdots+6)=3.5\,. \end{aligned} \] This is a formal confirmation of the experiment from Figure 5.9.

(b) Let \(X\) be the number of dots on the first roll and \(Y\) the number of dots on the second roll. Then according to (Theorem 5.40 (b)): \[ \begin{gathered} E(X+Y)=E(X)+E(Y)=3.5+3.5=7 \end{gathered} \] □

A gambling game is called fair if the expected value of the winnings \(G\) matches the stake.

Exercise 5.44 (Lottery) In the 6 out of 45 lottery, the stake for a bet is 10 currency units. How high must the victory for a main prize be in order for it to be a fair game of chance?

Solution: Let \(A\) be the event of scoring a main prize and \(G\) the achieved gain. For it to be a fair game, the equation \[ \begin{aligned} Stake &=E(G)=E(Winning Amount\cdot X_A)=\\ &= Winning Amount\cdot E(X_A)= Winning Amount\cdot P(A) \end{aligned} \] must hold. We applied the theorem (Theorem 5.40 (a) and (b)). It follows: \[ \begin{gathered} \frac{Stake}{P(A)}=Winning Amount \end{gathered} \] We have already calculated the probability \(P(A)\) for the main prize in Exercise 5.12. Therefore, for a fair bet, the winning amount must be: \[ \begin{gathered} \frac{10}{P(A)}=10\cdot\frac{45\cdot 44\cdots 43\cdot 40}{ 6\cdot 5\cdots 2\cdot 1}=81,450,600. \end{gathered} \]

Exercise 5.45 (Financial Mathematics) A security with an initial value of \(300\) increases by 5 percent with a probability of 0.2 within a year, or it decreases by 5 percent. Find the expected value of the value of this investment after one year.

Solution: Let \(W\) denote the value of the security after one year, and let \(A\) be the event that the security increases by 5 percent. We use indicators again. Then, \[ \begin{gathered} W=300\cdot 1.05 \cdot X_A+ 300\cdot 0.95 \cdot X_{A'}=315 X_A+285 X_{A'}. \end{gathered} \] The following results from the theorem Theorem 5.40: \[ \begin{aligned} E(W)&= 315 E(X_A)+285 E(X_{A'})=315 P(A)+285P(A')\\ &=315\cdot 0.2+285\cdot 0.8= 291. \end{aligned} \]

Expectation values of continuous random variables

These are defined by integrals. Specifically, if the continuous random variable \(X\) has the density \(f(x)\), then its expectation value is: \[ \begin{gathered} E(X)=\int_{-\infty}^\infty xf(x)\,\mathrm{d}x. \end{gathered} \tag{5.21}\] The calculation of these integrals typically requires advanced calculus methods, which is why we will not go into detail here. For completeness, we mention two special cases that we have already encountered in applications (see Example 5.24 and Example 5.26):

Theorem 5.46 If \(T\) is exponentially distributed with distribution function \(F(t)=1-e^{-\lambda t}, t\ge 0\), then \(E(T)=1/\lambda\).

If \(X\) is logistically distributed with distribution function \(F(x)=\dfrac{1}{1+e^{-(x-\mu)/s}}, X\in\mathbb R\), then \(E(X)=\mu\).

We now take a look at an interesting problem from the field of actuarial science.

A survival life insurance consists of a promise to pay out a capital \(K\) after a period of \(t\) years if the policyholder is still alive at that point. If \(A\) denotes the event that the policyholder survives the \(t\) year waiting period, then the payout is obviously \(K\cdot X_A\). The present value of the payout at the time the insurance is taken out is \(B=Kd^tX_A\), where \(d\) denotes the discount factor.

The risk of insurance is understood to be the expected value \(R=E(B)\) of the present value of the payout. If \(q\) is the mortality rate of the insured during a year, then (oversimplified) \(P(A)=(1-q)^t\) and therefore the risk of the insurance is \[ \begin{gathered} R=E(B)=Kd^t(1-q)^t. \end{gathered} \] The insurance principle states, that the premium of an insurance policy, i.e., the price paid by the policyholder, must match the risk of the insurance. In practice, an insurance premium also includes administrative fees and is therefore larger than a pure risk premium.

Exercise 5.47 (Insurance) Calculate the risk premium for a 40-year-old man and a 40-year-old woman who want to take out a survival life insurance for a capital of 100 000 CU, to be paid out after 10 years. The legally binding interest rate for insurance calculations is 3%.

The mortality rates are 0.003 for 40-year-old men \(q_m=0.003\) and 0.0015 for 40-year-old women \(q_w=0.0015\).

How high is the yield for a surviving policyholder from such an insurance contract?

Solution: For men, the risk premium is \[ \begin{gathered} R_m=100000 \left( \frac{1}{1.03}\right)^{10} (1-0.003)^{10}=72207. \end{gathered} \] The annual yield \(r\) results from \(K_{10}=K_0(1+r)^{10}=R_m(1+r)^{10}\) and is \[ \begin{gathered} \left(\frac{100000}{72207}\right)^{1/10}-1=0.0331. \end{gathered} \] For women, the risk premium is \[ \begin{gathered} R_m=100000 \left( \frac{1}{1.03}\right)^{10} (1-0.0015)^{10}=73301. \end{gathered} \] The yield is \[ \begin{gathered} \left(\frac{100000}{73301}\right)^{1/10}-1=0.0315. \end{gathered} \] □

5.3.3 The Multiplication Rule for Expected Values

The expected value has a remarkable multiplication property when applied to products of independent random variables.

The independence of events can be formulated mathematically as a multiplication property of probabilities. Something similar applies to random variables and their expected value.

This can be seen directly with indicator variables. If \(A\) and \(B\) are two events, then obviously \(X_{A\cap B}=X_AX_B\) because the event \(A\cap B\) only occurs if both events \(A\) and \(B\) happen at the same time. Then \(X_A=1\) and \(X_B=1\) and therefore \(X_AX_B=1\). This leads to \(E(X_AX_B)=E(X_{A\cap B})=P(A\cap B)\). Thus, we get \[ \begin{gathered} E(X_AX_B)=E(X_A)E(X_B)\quad \Leftrightarrow\quad P(A\cap B)=P(A)P(B). \end{gathered} \] So, the two events \(A\) and \(B\) are independent if and only if the formula \[ \begin{gathered} E(X_AX_B)=E(X_A)E(X_B). \end{gathered} \] is correct.

In general, the following statement holds.

Theorem 5.48 Let \(X\) and \(Y\) be two random variables that possess an expected value. If \(X\) and \(Y\) are independent, then it holds that \[ \begin{gathered} E(XY)=E(X)E(Y). \end{gathered} \tag{5.22}\]

5.3.4 The Variance of Random Variables

Let \(X\) be a random variable with the expected value \(E(X)=\mu\).

The expected value of a random variable provides information about the long-term average values of the random variable. However, the expected value does not tell us about how much the values of the random variable scatter around $. In order to get an idea of the spread of the values of a random variable, we are interested in the deviations \(X-\mu\) of the random variable from its expected value.

Definition 5.49 Let \(X\) be a random variable and \(\mu\) its expected value. The expected value of the random variable \((X-\mu)^2\) is called the variance of the random variable: \[ \begin{gathered} \sigma^2=V(X)=E (X-\mu)^2. \end{gathered} \] The square root \(\sigma=\sqrt{V(X)}\) is referred to as the standard deviation of \(X\).

A simplified formula is used for calculating variances, which reduces the computational effort.

Theorem 5.50 (Steiner’s Translation Theorem) The is a random variable \(X\) with the expected value \(E(X)=\mu\) and the variance \(V(X)\). Then it holds that \[ \begin{gathered} V(X)=E(X^2)-\mu^2. \end{gathered} \]

Justification: This follows directly from the Definition 5.49. When we perform the squaring: \[ \begin{aligned} V(X)&=E(X^2-2\mu X+\mu^2)=E(X^2)-2\mu E(X)+\mu^2\\[5pt] &=E(X^2)-2\mu^2+\mu^2=E(X^2)-\mu^2. \end{aligned} \] □

Exercise 5.51 Calculate the variance of the number on a die when it is thrown.

Solution: We already know \(E(X)=3.5\). Now we calculate \(E(X^2)\): \[ \begin{gathered} E(X^2)=\frac{1}{6}\left(1^2+2^2+3^2+4^2+5^2+6^2\right)=\frac{91}{6}=15.1667. \end{gathered} \] Then it follows (using Theorem 5.50) \[ \begin{gathered} V(X)=E(X^2)-\mu^2=\frac{91}{6}-\left(\frac{7}{2}\right)^2=\frac{35}{12}\simeq 2.9167. \end{gathered} \] □

In the next exercise, we revisit the process engineering problem from Exercise 5.35.

Exercise 5.52 A random variable \(X\) has the probability function: \[ \begin{gathered} \begin{array}{c|cccc} k & 0 & 1 & 2 & 3\\ \hline P(X=k) & 0.504 & 0.398 & 0.092 & 0.006 \end{array} \end{gathered} \] Calculate \(E(X)\) and \(V(X)\).

Solution: We first calculate \(\mu=E(X)\) and \(E(X^2)\): \[ \begin{aligned} \mu&=0\cdot 0.504+1\cdot 0.398+2\cdot 0.092+3\cdot 0.006=0.6,\\[4pt] E(X^2)&=0^2\cdot 0.504+1^2\cdot 0.398+2^2\cdot 0.092+3^2\cdot 0.006=0.82\,. \end{aligned} \] Following from that \[ \begin{gathered} V(X)=E(X^2)-\mu^2=0.82-0.6^2=0.46\,. \end{gathered} \] □

Remark 5.53 (Interpretation of Variance) As one can read from the definition of variance, the variance \(V(X)\) of a random variable \(X\) contains information about how much the random variable \(X\) can fluctuate around its expected value \(E(X)\). This information can be specified mathematically quite precisely.

Let \(\sigma=\sqrt{V(X)}\) denote the standard deviation of the random variable \(X\). One might then ask how large the deviations \(X-E(X)\) might be. This question can only be answered precisely if the distribution of \(X\) is known.

A probability distribution that surprisingly appears in many applications is the normal distribution (see Section 5.4). For normally distributed random variables, the following holds: \[ \begin{gathered} P(|X-E(X)|\le \sigma)\approx 0.66, \quad P(|X-E(X)|\le 2\sigma)\approx 0.95 \end{gathered} \] The standard deviation can thus be used to create rules of thumb which approximately indicate the fluctuation ranges of random variables: In the interval \((E(X)-\sigma,E(X)+\sigma)\) lie 66 percent of observed values of \(X\), etc.

However, the aforementioned rules are based on the characteristics of the normal distribution. In unfavorable cases, it may happen that the probabilities of the fluctuation intervals are significantly lower than indicated above.

We now turn to the rules for calculating variances. First, we examine how the variance changes when we subject a random variable to a linear transformation.

Theorem 5.54 Let \(X\) be a random variable with the variance \(V(X)\). Then it holds \[ \begin{gathered} V(aX+b)=a^2V(X) \quad \text{for $a,b \in \mathbb R$}. \end{gathered} \]

Justification: From the Definition 5.49 of variance it follows: \[ \begin{aligned} V(aX+b)&=E(aX+b-E(aX+b))^2=E(aX-aE(X))^2\\ &=a^2E(X-E(X))^2=a^2V(X). \end{aligned} \] Incidentally, it also follows from this that the variance of a constant is zero, that is \(V(b)=0\). □

Exercise 5.55 (Linear Cost Model) A manufacturing company operates with monthly fixed costs of 1000 monetary units (MU) and variable unit costs of 5 MU. The monthly production is a random variable with a standard deviation of 20 units. Find the variance and standard deviation of the monthly costs.

Solution: If \(X\) denotes the monthly production and \(Y\) the monthly costs, then it follows \(Y=1000+5X\). Consequently (since \(V(X)=20^2=400\)): \[ \begin{gathered} V(Y)=V(1000+5X)=25V(X)=25\cdot 400 =10\,000. \end{gathered} \] The standard deviation \(\sqrt{V(Y)}\) is 100. □

It is neither expected nor correct to say that the variance of a sum of random variables matches the sum of their individual variances. However, it is all the more remarkable that such an addition law for variances does hold for independent random variables.

Theorem 5.56 If \(X\) and \(Y\) are independent random variables, then it holds that \[ \begin{aligned} V(X+Y)&=V(X)+V(Y). \end{aligned} \]

Justification: We begin our calculation and once again use Definition 5.49: \[ \begin{gathered} \begin{array}{rcl} V(X+Y) & = & E(X+Y - E(X+Y))^2 \\ & = & E(X-E(X) +Y-E(Y))^2\\ & = & E(X-E(X))^2 +2E\left[(X-E(X))(Y-E(Y))\right]\\ & & +E(Y-E(Y))^2. \end{array} \end{gathered} \] But for the middle part, due to the multiplication property (5.22), we have \[ \begin{gathered} E\left[(X-E(X))(Y-E(Y))\right]=E(X-E(X))E(Y-E(Y))=0, \end{gathered} \] because \(E(X-E(X))=E(X)-E(E(X))=E(X)-E(X)=0\). □

Interestingly, the addition rule also applies when we consider differences of independent random variables, because \[ \begin{aligned} V(X-Y) & = V(X)+V\left((-1)Y\right)\\ & = V(X)+(-1)^2V(Y)=V(X)+V(Y). \end{aligned} \]

5.3.5 The Return of a Portfolio

The addition rule for variances has an important application in financial mathematics. It implies that in the formation of portfolios of securities, diversification leads to a reduction in risk.

The return \(R\) of a security refers to the relative increase in value during a period. If at the beginning the value of the security was \(V_0\) monetary units and at the end of the period the value is \(V_1\) monetary units, then the return achieved with this investment in one period is \[ \begin{gathered} R=\frac{V_1-V_0}{V_0}. \end{gathered} \] A portfolio is a decision about how available capital is invested in two or more securities. Assume we form a portfolio of three securities \(A, B\), and \(C\). At the beginning of the period, we decide to invest the sums \(A_0,\;B_0,\;C_0\) in these papers. If at the end of the period these investments have values of \(A_1, B_1\), and \(C_1\), then the joint return \(R\) of the portfolio formed in this way is the relative change in value of the invested sum: \[ \begin{aligned} R&=\dfrac{A_1+B_1+C_1-(A_0+B_0+C_0)}{A_0+B_0+C_0}. \end{aligned} \tag{5.23}\] We set: \[ \begin{gathered} R_A=\frac{A_1-A_0}{A_0},\quad R_B=\frac{B_1-B_0}{B_0},\quad R_C=\frac{C_1-C_0}{C_0}, \end{gathered} \] these are the returns of the three securities. We can now express the joint return \(R\) with the help of the returns \(R_A, R_B\), and \(R_C\): \[ \begin{gathered} \begin{array}{rcl} R & = & \displaystyle \frac{A_1-A_0}{A_0+B_0+C_0} + \frac{B_1-B_0}{A_0+B_0+C_0} + \frac{C_1-C_0}{A_0+B_0+C_0}\\[4pt] & = & \displaystyle \frac{A_0}{A_0+B_0+C_0} \cdot \frac{A_1-A_0}{A_0} + \frac{B_0}{A_0+B_0+C_0} \cdot \frac{B_1-B_0}{B_0}+\\[4pt] & & \displaystyle \frac{C_0}{A_0+B_0+C_0} \cdot \frac{C_1-C_0}{C_0}\\[4pt] & = & \displaystyle \frac{A_0}{A_0+B_0+C_0} \cdot R_A + \frac{B_0}{A_0+B_0+C_0} \cdot R_B +\\[4pt] & & \displaystyle \frac{C_0}{A_0+B_0+C_0} \cdot R_C. \end{array} \end{gathered} \] The joint return is therefore the weighted average of the individual returns, where the capital shares (percentages) of the individual securities are to be used as weights: \[ \begin{gathered} \alpha=\frac{A_0}{A_0+B_0+C_0},\quad \beta=\frac{B_0}{A_0+B_0+C_0},\quad \gamma=\frac{C_0}{A_0+B_0+C_0} \end{gathered} \] In other words, the joint return of our portfolio is: \[ \begin{gathered} R=\alpha R_A+\beta R_B+\gamma R_C,\quad\text{where }\alpha+\beta+\gamma=1. \end{gathered} \tag{5.24}\] It is precisely these capital shares \(\alpha, \beta\), and \(\gamma\) that define the portfolio.

But why should investors form portfolios at all? Wouldn’t it be more sensible to invest all the capital in the paper that yields the highest return?

The main reason for the formation of a portfolio is that for most investment forms, the possible returns are not deterministic sizes but random variables. And it is the variance of the return that is important, for it is a measure of the risk associated with a financial investment. The higher the variance of the return, the riskier it is to invest in a security.

We can illustrate this intuitively as follows: suppose we have the choice between two securities \(A\) and \(B\) with returns \(R_A\) and \(R_B\). Further suppose that the expected returns are the same, so \(E(R_A)=E(R_B)\), but for the variances it should hold: \[ \begin{gathered} V(R_A)=0,\quad V(R_B)>0. \end{gathered} \] In this case, we have good reasons to prefer security \(A\), because although the average yield is the same, the yield achieved with paper \(B\) is associated with some uncertainty, which is greater the larger \(V(R_B)\). In fact, investments with a variance of zero in returns are called risk-free. These are, therefore, securities where the return over a certain period is guaranteed.

We now calculate the expected value and variance of \(R\), given in (5.24). The expected return is due to the linearity of the expectation value (Theorem 5.40 (b)): \[ \begin{gathered} E(R)=\alpha E(R_A)+\beta E(R_B)+\gamma E(R_C). \end{gathered} \] If the returns \(R_A,R_B\), and \(R_C\) are independent random variables, then the variance—and thus a measure of the risk associated with the portfolio—is due to Theorem 5.54 and Theorem 5.56: \[ \begin{gathered} V(R)=\alpha^2V(R_A)+\beta^2V(R_B)+\gamma^2V(R_C). \end{gathered} \tag{5.25}\] This formula, which follows from the law of variances addition, has remarkable consequences. It explains why it is sensible to diversify.

The next example shows the risk-reducing effect very clearly.

Exercise 5.57 (Diversification) An investor forms a portfolio from three securities \(A, B\), and \(C\). They invest 50% of the available funds in security \(A\), 30% in security \(B\), and 20% in security \(C\). The returns of these securities are independent random variables with the expected values 0.08, 0.05, and 0.03 and the same standard deviation of 0.02. Calculate the expected value and standard deviation of the return of this portfolio.

Solution: The return of the portfolio is \(R=0.5\cdot R_A+0.3\cdot R_B+0.2\cdot R_C\).

From this we have: \[ \begin{gathered} E(R)=0.5\cdot 0.08+0.3\cdot 0.05+0.2\cdot 0.03= 0.0610\,. \end{gathered} \] and \[ \begin{aligned} V(R)&=0.5^2\cdot V(R_A)+0.3^2\cdot V(R_B)+0.2^2\cdot V(R_C)\\ &=\left[0.5^2+0.3^2+0.2^2\right]\cdot 0.02^2=0.000152\,. \end{aligned} \] The standard deviation of the return is therefore \(\sqrt{0.000152}=0.012329\). It is thus substantially lower than the standard deviation of the return of each of the three securities. This means that the investment risk was significantly reduced by forming the portfolio. □

Remark 5.58 Three remarks or questions regarding this task:

• In this task and in deriving (5.25), we explicitly assumed that the returns of the securities are independent random variables. What if this assumption does not hold?

• In the task, the capital shares defining the portfolio were predetermined. But couldn’t we make these into decision variables and thus ask: what would an optimal portfolio look like?

• For the capital shares \(\alpha, \beta,\) and \(\gamma\), it is of course true that \(\alpha+\beta+\gamma=1\), but that does not mean that all three capital shares must be positive. Do negative capital shares make sense at all, and what do they mean?

These are very exciting questions that we will explore in detail in Chapter 9.

Exercise 5.59 An investor wants to form a portfolio from two securities, \(A\) and \(B\), whose returns are independent random variables. The standard deviations of the returns are known to them: \(\sigma(R_A)=0.7\) and \(\sigma(R_B)=0.8\). How should they choose the capital shares of the two securities in the portfolio so that the investment risk is minimized?

Solution: Let \(\alpha\) be the capital share of \(A\), then the share of \(B\) is \(1-\alpha\). The joint return is therefore \(R=\alpha R_A+(1-\alpha) R_B\). The measure of the risk is the variance of \(R\): \[ \begin{aligned} V(R)&=V(\alpha R_A+(1-\alpha)R_B)=\alpha^2V(R_A)+(1-\alpha)^2V(R_B)\to\min. \end{aligned} \]

We form the first derivative with respect to \(\alpha\) and set it to zero: \[ \begin{gathered} V'(R)=2\left[\alpha V(R_A)-(1-\alpha)V(R_B)\right]=0,\\[5pt] \alpha=\frac{V(R_B)}{V(R_A)+V(R_B)}=\frac{0.8^2}{0.7^2+0.8^2}=0.5664\,. \end{gathered} \] Optimal capital shares would therefore be 56.6% for \(A\) and 43.4% for \(B\). The fact that this actually guarantees the minimum of the variance is shown by the 2nd derivative \(V''(R)=2(V(R_A)+V(R_B))>0\). □

5.3.6 The Variance of the Arithmetic Mean

The reduction in variance is especially drastic when calculating means.

Let \(X\) be a random variable with the expected value \(E(X)=\mu\) and variance \(V(X)=\sigma^2\) in a random experiment. We conduct \(n\) independent repetitions of the random experiment and observe \(n\) copies \(X_1,\,X_2,\ldots,\,X_n\) of the random variable \(X\). We denote the mean of these random variables with \[ \begin{gathered} \overline{X}=\frac{X_1+X_2+\cdots+X_n}{n}\,. \end{gathered} \]

Theorem 5.60 If \(X\) is a random variable with \(E(X)=\mu\) and \(V(X)=\sigma^2\), then it follows that \[ \begin{gathered} E(\overline{X})=\mu, \qquad V(\overline{X})=\frac{\sigma^2}{n}. \end{gathered} \]

Justification: For the expected value, we obtain \[ \begin{aligned} E(\overline{X}) & = E\left(\frac{X_1+X_2+\ldots+X_n}{n}\right) \\ & = \frac{1}{n}(\underbrace{\mu+\ldots+\mu}_{n\text{ terms}})=\frac{n\mu}{n}=\mu. \end{aligned} \] For the variance, it holds that \[ \begin{aligned} V(\overline{X}) & = V\left(\frac{X_1+X_2+\ldots+X_n}{n}\right) \\ & = \frac{1}{n^2}(\underbrace{\sigma^2+\ldots+\sigma^2}_{n\text{ terms}})=\frac{n\sigma^2}{n^2}=\frac{\sigma^2}{n}\,. \end{aligned} \] Note that the assumption of independence is crucial here! □

Theorem 5.60 is of fundamental importance in statistics. Here, the expected value \(\mu\) of a variable (random variable) \(X\) is typically unknown, and one wants to obtain information about \(\mu\) based on samples. The arithmetic mean is one way to do this, and it is surprisingly good. For Theorem 5.60 holds two important messages:

1. The arithmetic mean is unbiased, which is the statement of \(E(\overline{X}) = \mu\). Therefore, we can trust that \(\overline{X}\) neither systematically overestimates nor underestimates the unknown \(\mu\).

2. With an increasing sample size \(V(\overline{X}) = \sigma^2/n \to 0\), this means that \(\overline{X}\) becomes more accurate as the sample size increases. With a very large number of observations, the mean therefore almost coincides with the expected value. This subsequently justifies our introductory intuitive explanation of the expected value.

The circumstance (b) that the variance of a mean decreases with an increasing number of observations is also called the law of large numbers.

Exercise 5.61 (Quality Control) In a production process, workpieces are produced with a prescribed length. The standard deviation of the length is \(3\) mm. To monitor compliance with the expected value of the length, the average length of a series of \(n\) workpieces is checked. How large must the series be so that the standard deviation of the average length is \(0.5\) mm?

Solution: The average length of a series is given by the mean, and the variance of the mean is \(V(\overline{X}) = \sigma^2 / n\). Therefore, the standard deviation of the average length of a series of \(n\) workpieces is \(3/\sqrt{n}\). To achieve that \[ \begin{gathered} \frac{3}{\sqrt{n}} = 0.5 \end{gathered} \] \(\sqrt{n}=6\) must be, therefore \(n=36\) is required. □

5.4 The Normal Distribution

The normal distribution is one of the most important, if not the most important probability distribution. The term normal distribution probably goes back to Lambert Adolphe Jacques Quetelet (1796-1876), a Belgian statistician who (like others before him) had noticed in his studies that many frequency distributions of biological characteristics, such as the height of people, showed a typical bell-shaped curve.

The normal distribution is a continuous distribution, which is determined by only two parameters, namely its expected value \(\mu\) and its variance \(\sigma^2\).

Definition 5.62 A random variable \(X\) is said to be normally distributed if its density function is given by: \[ \begin{gathered} f(x) = %\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} = \frac{1}{\sigma\sqrt{2\pi}}\exp\left[-\frac{(x-\mu)^2}{2\sigma^2}\right]. \end{gathered} \tag{5.26}\] It holds that: \(E(X)=\mu\) and \(V(X)=\sigma^2\).

The density \(f(x)\) shows a beautiful bell-shaped form, symmetric around the expected value \(\mu\). The greater the standard deviation \(\sigma\), the flatter the density curve, and the smaller \(\sigma\), the more \(f(x)\) is centered around \(\mu\).

Figure 5.10: Density of the normal distribution.

Probabilities, as already explained above, are defined by areas under the density curve: \[ \begin{gathered} P(a<X\le b)=\int_a^bf(x)\,\mathrm{d}x. \end{gathered} \] Unfortunately, it is not possible to express the cumulative distribution function \(F(x)=P(X\le x)\) using a finite number of terms in a closed form. Therefore, probabilities must be determined numerically. This makes use of the fact that linear transformations of normally distributed random variables are themselves normally distributed. In particular, the random variable \(Z\), defined by \[ \begin{gathered} Z=\frac{X-\mu}{\sigma}, \end{gathered} \tag{5.27}\] is normally distributed with mean \(\mu=0\) and standard deviation \(\sigma=1\). The transformation (5.27) is called standardization, and the distribution of \(Z\) is known as the standard normal distribution.

5.4.1 The Standard Normal Distribution

The density of a standard normally distributed random variable \(Z\) is denoted by \(\phi(z)\): \[ \begin{gathered} \phi(z)=\frac{1}{\sqrt{2\pi}}e^{-z^2/2}. \end{gathered} \] The graph of \(\phi(z)\) can be seen in Figure 5.10 (left). The cumulative distribution function is: \[ \begin{gathered} P(Z\le a)=\Phi(a)=\int_{-\infty}^a\phi(z)\,\mathrm{d}z,\qquad a\in\mathbb R. \end{gathered} \] The function values \(\Phi(z)\) can be calculated using computer programs or looked up in tables, see Section 5.4.4. Their use is very simple, the following rules apply: \[ \begin{aligned} P(Z\le a) & = \Phi(a), \end{aligned} \tag{5.28}\] \[ \begin{aligned} P(a<Z\le b) & = \Phi(b)-\Phi(a). \end{aligned} \tag{5.29}\] Because of the symmetry of the standard normal distribution’s density around zero, it is additionally true that: \[ \begin{gathered} \Phi(0)=0.5,\qquad \Phi(-a)=1-\Phi(a)\quad\text{for all }a\in\mathbb R. \end{gathered} \tag{5.30}\] The following example exercise demonstrates how this table is used.

Exercise 5.63 A random variable \(Z\) is standard normally distributed. To be calculated using Section 5.4.4: \[ \begin{gathered} \begin{array}{clccl} (a) & P(Z\le 1) & \quad & (b) & P(Z>-0.8) \\[3pt] (c) & P(-0.5<Z\le2) & \quad & (d) & P(|Z|\le 1.2) \\[3pt] (e) & P(|Z|>2) & \quad & (f) & P(Z^2<2) \\[3pt] (g) & P(3Z-1> 2) & \quad & (h) & P(4-Z\le Z) \\[3pt] (i) & P(|2Z+1|<1) \end{array} \end{gathered} \]

Solution:

(a) Here, we are directly looking for the value of the cumulative distribution function:

(b) We first address the complementary event:

(c) This is a direct application of the rule (5.29):

(d) To calculate this probability, it is first necessary to solve the inequality \(|Z|\le 1.2\). This is easy: all real numbers in the interval \([-1.2,1.2]\) have the property \(|Z|\le 1.2\). That is, the events \(\{|Z|\le 1.2\}\) and \(\{-1.2\le Z\le 1.2\}\) are equivalent and therefore have the same probability:

(e) follows completely analogously to (d): we only consider the complementary event beforehand: \[ \begin{aligned} P(|Z|>2)&=1-P(|Z|\le 2) = 1 - P(-2\le Z\le 2)\\[4pt] &=1-\left[\Phi(2)-\Phi(-2)\right]\\[4pt] &= 1-[0.977-0.023]=0.046 \end{aligned} \] (f) To use Table 1, we first have to solve the quadratic inequality (Z^2<2). All real numbers in the interval ((-1.41, +1.41)) satisfy this inequality. Therefore: \[ \begin{aligned} P(Z^2<2)&= P(-\sqrt{2}<Z<\sqrt{2})\simeq \Phi(1.41)-\Phi(-1.41)\\ &=0.921-0.079=0.842,\end{aligned} \] here we rounded () to two decimal places, as Table 1 does not allow for higher precision.

(g) We solve the inequality \[ \begin{gathered} 3Z-1>2\implies 3Z>3\implies Z>1. \end{gathered} \] Therefore: \[ \begin{aligned} P(3Z-1>2)&=P(Z>1)=1-P(Z\le 1) \\ &=1-\Phi(1)=1-0.841=0.159 \end{aligned} \]

(h) From (4-ZZ) it follows that (42ZZ). Thus: \[ \begin{aligned} P(4-Z\le Z)&=P(Z\ge 2)=1-P(Z<2)\\ &=1-\Phi(2)=1-0.977=0.023 \end{aligned} \] (i) Compare with (d): \[ \begin{aligned} P(|2Z+1|<1)&=P(-1<2Z+1<1)=P(-2<2Z<0)\\ &=P(-1<Z<0)=\Phi(0)-\Phi(-1)\\ &=0.5-0.159=0.341 \end{aligned} \]

Quantiles

Many application problems require the calculation of so-called quantiles of the standard normal distribution. This involves solving equations of the form \[ \begin{gathered} P(Z\le z)=\Phi(z)=\alpha, \end{gathered} \] where ((0,1)) is given and (z) is sought. The solution to this problem is the ()-quantile. The ()-quantile is therefore that value (z) which the random variable does not exceed with probability (). In other words, the quantile is the inverse function (^{-1}) of the distribution function ().

Definition 5.64 The \(\alpha\)-quantile \(\Phi^{-1}(\alpha)\) of the standard normal distribution satisfies the equation \[ \begin{gathered} P(Z\le \Phi^{-1}(\alpha))=\alpha,\qquad \alpha\in(0,1). \end{gathered} \] This means: \[ \begin{gathered} \Phi(z)=\alpha \Leftrightarrow z=\Phi^{-1}(\alpha). \end{gathered} \]

The \(\alpha\)-quantile divides the area under the density curve of the standard normal distribution into two parts, with the left part having an area of \(\alpha\) and the right part having an area of \(1-\alpha\). The Figure 5.11 illustrates the concept of the quantile.

Figure 5.11: The \(\alpha\)-quantile.

Since the density of the standard normal distribution is symmetric about zero, it follows that: \[ \begin{gathered} \Phi^{-1}(0.5)=0,\quad \Phi^{-1}(\alpha)=-\Phi^{-1}(1-\alpha). \end{gathered} \]

For quantiles of the standard normal distribution, one either uses computer programs or tables, see Section 5.4.4.

Exercise 5.65 The random variable \(Z\) follows a standard normal distribution.

1. Find the value that \(Z\) does not exceed with a probability of 0.9.

2. Find the value that \(Z\) exceeds with a probability of 0.6.

3. Find an \(a\) such that \(P(-a<Z\le a)=0.84\).

Solution:

(a) \(P(Z\le z)=\Phi(z)=0.9 \implies z=\Phi^{-1}(0.9)=1.2816.\)

(b) \(P(Z>z)=0.6 \implies P(Z\le z)=\Phi(z)=0.4 \implies z=\Phi^{-1}(0.4)=-0.2533.\)

(c) We use the symmetry rule (5.30), \(\Phi(-a)=1-\Phi(a)\): \[ \begin{aligned} P(-a<Z\le a)&=0.84\\ \Phi(a)-\Phi(-a)&=0.84\\ \Phi(a)-\left[1-\Phi(a)\right]&=0.84\qquad\text{(Symmetry rule)}\\ 2\Phi(a)&=1.84\\ \Phi(a)&=0.92\qquad\implies a=\Phi^{-1}(0.92)=1.4051\,. \end{aligned} \]

5.4.2 Applications of the Normal Distribution

We are often faced with the problem of calculating probabilities associated with a random variable without knowing the exact distribution of the variable. In such cases, it is helpful if we know that the random variable \(X\) is approximately normally distributed with known mean \(\mu\) and variance \(\sigma^2\). In these situations, probabilities and quantiles are calculated by standardizing \[ \begin{gathered} Z=\frac{X-\mu}{\sigma} \end{gathered} \] using the standard normal distribution.

Exercise 5.66 (Intelligence Tests) The Intelligence Quotient (IQ) is excellently approximated as normally distributed in a population with \(\mu=100\) and \(\sigma=15\).

1. Someone is considered highly gifted if they have an \(\mathit{IQ}>130\). What is the proportion of the highly gifted in the population?

2. What IQ would one need to achieve on a test to belong to the top-25%?

3. Within what symmetric interval around the mean do \(2/3\) of the population lie?

Solution:

(a) \(P(\mathit{IQ}>130)=1-P(\mathit{IQ}\le 130)\), so it is sufficient to calculate the probability \(P(\mathit{IQ}\le 130)\). To do this, we standardize: \[ \begin{aligned} P(\mathit{IQ}\le 130)&=P\left(\underbrace{\frac{\mathit{IQ}-100}{15}}_{Z}\le \frac{130-100}{15}\right)=P\left(Z\le 2\right). \end{aligned} \] The random variable \(Z=\dfrac{\mathit{IQ}-100}{15}\) is however standard normally distributed. This means: \[ \begin{aligned} P\left(Z\le 2\right)&=\Phi(2)=0.977, \end{aligned} \] and therefore the proportion of highly gifted individuals is \(1-0.977=0.023\), i.e., 2.3 %.

(b) We are looking for a critical test result \(a\), such that \(P(\mathit{IQ}>a)=0.25\), or via the opposite event: \(P(\mathit{IQ}\le a)=0.75\). We standardize again: \[ \begin{aligned} P(\mathit{IQ}\le a)&=P\left(\frac{\mathit{IQ}-100}{15}\le \frac{a-100}{15}\right) =0.75, \end{aligned} \] or: \[ \begin{aligned} P\left(Z\le \frac{a-100}{15}\right)&=\Phi\left(\frac{a-100}{15}\right)=0.75\,. \end{aligned} \] We solve the last equation using the inverse function \(\Phi^{-1}\): \[ \begin{gathered} \frac{a-100}{15}=\Phi^{-1}(0.75)=0.6745\\ \implies a=100+15\cdot 0.6745=110.1175\,. \end{gathered} \] Someone would have to score at least 110 to be among the top 25% of the population.

(c) The interval we are looking for is of the form \([100-a, 100+a]\). The probability of falling into this interval must be \(2/3\): \[ \begin{gathered} P(100-a\le \mathit{IQ}\le 100+a)=\frac{2}{3},\\[4pt] P\left(\frac{100-a-100}{15}\le \frac{\mathit{IQ}-100}{15} \le \frac{100+a-100}{15}\right)=\frac{2}{3},\\[4pt] P\left(-\frac{a}{15}\le Z\le \frac{a}{15}\right)=\frac{2}{3}\,. \end{gathered} \] We now simplify this with the symmetry rule (5.30): \[ \begin{gathered} \Phi\left(\frac{a}{15}\right)-\Phi\left(-\frac{a}{15}\right)=\frac{2}{3},\\[4pt] \Phi\left(\frac{a}{15}\right)-\left[1-\Phi\left(\frac{a}{15}\right)\right]=\frac{2}{3},\\[4pt] \Phi\left(\frac{a}{15}\right)=\frac{5}{6}=0.8333\implies \frac{a}{15}=\Phi^{-1}(0.83)=0.9542,\\[4pt] a=15\cdot 0.9542=14.3130\simeq 14. \end{gathered} \] That means: in the interval \([100\pm 14]=[86,114]\) lies approximately 2/3 of the population. □

Exercise 5.67 (Financial Mathematics) The return of a security is normally distributed with a mean of 0.08 and a standard deviation of 0.05.

1. How likely is it that the return is negative?

2. What value is exceeded by the return with a probability of 1 percent?

Solution: Let \(X\) be the return of the security.
(a) We are interested in \(P(X<0)\): \[ \begin{aligned} P(X<0) & = P\left(Z<\frac{0-0.08}{0.05}\right)\\ & = P(Z<-1.6) = \Phi(-1.6)=0.055. \end{aligned} \] (b) We are looking for \(x\) such that \(P(X<x)=0.01\). \[ \begin{gathered} P(X<x)=P\left(Z\le \frac{x-0.08}{0.05}\right)=0.01\\[4pt] \frac{x-0.08}{0.05}=\Phi^{-1}(0.01)=-2.3263\\ \implies x=0.08-0.05\cdot 2.3263 =-0.0363\,. \end{gathered} \]

□

Exercise 5.68 The daily electricity consumption of a company (in MWh) is approximately normally distributed with a mean of 6.5 and a variance of 4.6. An own power supply for this business provides 8 MWh daily. How likely is the company to be self-sufficient on a particular day?

Solution: Let \(X\) be the daily power consumption. Then \[ \begin{gathered} P(X\le 8)=P\left(Z\le\frac{8-6.5}{\sqrt{4.6}}\right)= P(Z\le 0.7)=0.758\,. \end{gathered} \] The probability that on a particular day no more than 8 MWh are consumed is about \(76\%\). □

Exercise 5.69 The annual demand for a product is a normally distributed random variable with an expected value of 280 and a variance of 1600. How many units must be produced so that the probability that the demand exceeds the produced amount is only 1 percent?

Solution: Let \(X\) be the annual demand and \(x\) be the produced quantity. We are interested in that value of \(x\) for which \(P(X>x)=0.01\). Since \[ \begin{gathered} P(X>x)=P\left(Z>\frac{x-280}{\sqrt{1600}}\right)=0.01 \end{gathered} \] is supposed to occur, it follows: \[ \begin{gathered} P\left(Z\le\frac{x-280}{40}\right)=0.99\implies \frac{x-280}{40}=\Phi^{-1}(0.99)=2.3263. \end{gathered} \] Therefore, the required production quantity is: \[ \begin{gathered} x=280+40\cdot 2.3263=373.05\text{ units}. \end{gathered} \] □

5.4.3 The Central Limit Theorem

The assumption of a normal distribution is particularly justified when it comes to the probability distribution of sums and averages. The reason for this is the central limit theorem, another fundamental principle of probability theory, alongside the law of large numbers.

Theorem 5.70 (Central Limit Theorem) Let \(X\) be a random variable with \(E(X)=\mu\) and \(V(X)=\sigma^2\). Then the sum \(S_n\) and the average \(\overline{X}\) of \(n\) independent copies of the random variable are approximately normally distributed, where: \[ \begin{aligned} E(S_n)&=n\mu & V(S_n)&=n\sigma^2, \\ \end{aligned} \tag{5.31}\]

\[ \begin{aligned} E(\overline{X})&=\mu & V(\overline{X})&=\frac{\sigma^2}{n}\,. \end{aligned} \tag{5.32}\]

We lack the mathematical tools to prove this fundamental fact of probability theory here. However, applying the central limit theorem is very straightforward.

Exercise 5.71 (Quality Control) In a production process, workpieces with a prescribed length of \(1\) \(m\) are produced. The standard deviation of the length is \(3\) mm. To monitor compliance with the expected value of the length, the average length of a series of \(50\) workpieces is checked. What is the probability that this measurement is within the range of \(1000\pm 1\) mm, assuming the expected value of a workpiece’s length is indeed \(1\) \(m\)?

Solution: We calculate in the unit of 1 mm. Because of (5.31): \[ \begin{gathered} n=50,\qquad E(\overline{X})=1000,\qquad V(\overline{X})=\frac{3^2}{50}=0.18\,. \end{gathered} \] The probability that \(\overline{X}\) falls into the given tolerance interval \(1000\pm 1\) is: \[ \begin{aligned} P(999<\overline{X}< 1001) &=P\left(\frac{999-1000}{\sqrt{0.18}}<Z< \frac{1001-1000}{\sqrt{0.18}}\right)\\[4pt] &=P(-2.36<Z< 2.36) \\[4pt] &=\Phi(2.36)-\Phi(-2.36)\\[4pt] &=0.991-0.009=0.982\,. \end{aligned} \] □

5.4.4 Calculation of the Standard Normal Distribution

As mentioned several times in this section, for the calculation of probabilities or quantiles of the (standard) normal distribution, computer programs are usually used in practice. These programs offer the following two functions:

• Distribution function: \(\Phi(x) = \mathsf{P}(Z \le x) = \alpha\).
• Quantile function (or inverse distribution function): \(\Phi^{-1}(\alpha) = x\).

While the density function \(\phi(x)\) of the standard normal distribution can be easily calculated using the exponential function with a calculator, this is not the case for the distribution function and its inverse. Therefore, the following lists some ways to calculate these two functions. In addition to various computer programs, tables are also provided in which probabilities or quantiles can be looked up.

Tables

• Distribution function: In the first following table, the values of \(\Phi(x)\) are entered for \(x\) with two decimal places from \(-2.99, \dots, 2.99\).
• Quantile function: In the second following table, the values of \(\Phi^{-1}(\alpha)\) are entered for \(\alpha\) with two decimal places from \(0.01, \dots, 0.99\) as well as \(0.975\) and \(0.995\).

R

• Cumulative Distribution Function: pnorm(x)
• Quantile Function: qnorm(alpha)

Additionally, both functions can specify a different mean than the default mean = 0 as well as a different standard deviation than sd = 1. Further details are documented on ?pnorm.

GeoGebra (CAS Mode)

• Cumulative Distribution Function: Normal(0, 1, x)
• Quantile Function: InverseNormal(0, 1, alpha)

The expected value (mew) and the standard deviation (sigma) must always be specified. Therefore, the code above uses 0 and 1 to obtain the standard normal distribution.

Excel & LibreOffice

• Cumulative Distribution Function: NORM.S.VERT(x, 1) (German) or
  NORM.S.DIST(x, 1) (English)
• Quantile Function: NORM.S.INV(alpha)

The 1 at the end of the VERT/DIST function call indicates that the cumulative distribution function is to be calculated. Setting this value to 0 calculates the probability density function.

In addition to the functions with .S. in the name (for the standard normal distribution), there are also analogous functions for normal distributions where mean and standard deviation must be specified.

• Cumulative Distribution Function: NORM.VERT(x, 0, 1, 1) (German) or
  NORM.DIST(x, 0, 1, 1) (English)
• Quantile Function: NORM.INV(alpha, 0, 1)

WolframAlpha

• Cumulative Distribution Function: CDF[NormalDistribution[0, 1], x]
• Quantile Function: InverseCDF[NormalDistribution[0, 1], alpha]

The expected value and the standard deviation must always be specified. Therefore, the code above uses 0 and 1 to obtain the standard normal distribution.

Cumulative Distribution Function of the Standard Normal Distribution

	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
-2.9	0.002	0.002	0.002	0.002	0.002	0.002	0.002	0.001	0.001	0.001
-2.8	0.003	0.002	0.002	0.002	0.002	0.002	0.002	0.002	0.002	0.002
-2.7	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003
-2.6	0.005	0.005	0.004	0.004	0.004	0.004	0.004	0.004	0.004	0.004
-2.5	0.006	0.006	0.006	0.006	0.006	0.005	0.005	0.005	0.005	0.005
-2.4	0.008	0.008	0.008	0.008	0.007	0.007	0.007	0.007	0.007	0.006
-2.3	0.011	0.010	0.010	0.010	0.010	0.009	0.009	0.009	0.009	0.008
-2.2	0.014	0.014	0.013	0.013	0.013	0.012	0.012	0.012	0.011	0.011
-2.1	0.018	0.017	0.017	0.017	0.016	0.016	0.015	0.015	0.015	0.014
-2.0	0.023	0.022	0.022	0.021	0.021	0.020	0.020	0.019	0.019	0.018
-1.9	0.029	0.028	0.027	0.027	0.026	0.026	0.025	0.024	0.024	0.023
-1.8	0.036	0.035	0.034	0.034	0.033	0.032	0.031	0.031	0.030	0.029
-1.7	0.045	0.044	0.043	0.042	0.041	0.040	0.039	0.038	0.038	0.037
-1.6	0.055	0.054	0.053	0.052	0.051	0.049	0.048	0.047	0.046	0.046
-1.5	0.067	0.066	0.064	0.063	0.062	0.061	0.059	0.058	0.057	0.056
-1.4	0.081	0.079	0.078	0.076	0.075	0.074	0.072	0.071	0.069	0.068
-1.3	0.097	0.095	0.093	0.092	0.090	0.089	0.087	0.085	0.084	0.082
-1.2	0.115	0.113	0.111	0.109	0.107	0.106	0.104	0.102	0.100	0.099
-1.1	0.136	0.133	0.131	0.129	0.127	0.125	0.123	0.121	0.119	0.117
-1.0	0.159	0.156	0.154	0.152	0.149	0.147	0.145	0.142	0.140	0.138
-0.9	0.184	0.181	0.179	0.176	0.174	0.171	0.169	0.166	0.164	0.161
-0.8	0.212	0.209	0.206	0.203	0.200	0.198	0.195	0.192	0.189	0.187
-0.7	0.242	0.239	0.236	0.233	0.230	0.227	0.224	0.221	0.218	0.215
-0.6	0.274	0.271	0.268	0.264	0.261	0.258	0.255	0.251	0.248	0.245
-0.5	0.309	0.305	0.302	0.298	0.295	0.291	0.288	0.284	0.281	0.278
-0.4	0.345	0.341	0.337	0.334	0.330	0.326	0.323	0.319	0.316	0.312
-0.3	0.382	0.378	0.374	0.371	0.367	0.363	0.359	0.356	0.352	0.348
-0.2	0.421	0.417	0.413	0.409	0.405	0.401	0.397	0.394	0.390	0.386
-0.1	0.460	0.456	0.452	0.448	0.444	0.440	0.436	0.433	0.429	0.425
0.0	0.500	0.500	0.500	0.500	0.500	0.500	0.500	0.500	0.500	0.500
0.1	0.540	0.544	0.548	0.552	0.556	0.560	0.564	0.567	0.571	0.575
0.2	0.579	0.583	0.587	0.591	0.595	0.599	0.603	0.606	0.610	0.614
0.3	0.618	0.622	0.626	0.629	0.633	0.637	0.641	0.644	0.648	0.652
0.4	0.655	0.659	0.663	0.666	0.670	0.674	0.677	0.681	0.684	0.688
0.5	0.691	0.695	0.698	0.702	0.705	0.709	0.712	0.716	0.719	0.722
0.6	0.726	0.729	0.732	0.736	0.739	0.742	0.745	0.749	0.752	0.755
0.7	0.758	0.761	0.764	0.767	0.770	0.773	0.776	0.779	0.782	0.785
0.8	0.788	0.791	0.794	0.797	0.800	0.802	0.805	0.808	0.811	0.813
0.9	0.816	0.819	0.821	0.824	0.826	0.829	0.831	0.834	0.836	0.839
1.0	0.841	0.844	0.846	0.848	0.851	0.853	0.855	0.858	0.860	0.862
1.1	0.864	0.867	0.869	0.871	0.873	0.875	0.877	0.879	0.881	0.883
1.2	0.885	0.887	0.889	0.891	0.893	0.894	0.896	0.898	0.900	0.901
1.3	0.903	0.905	0.907	0.908	0.910	0.911	0.913	0.915	0.916	0.918
1.4	0.919	0.921	0.922	0.924	0.925	0.926	0.928	0.929	0.931	0.932
1.5	0.933	0.934	0.936	0.937	0.938	0.939	0.941	0.942	0.943	0.944
1.6	0.945	0.946	0.947	0.948	0.949	0.951	0.952	0.953	0.954	0.954
1.7	0.955	0.956	0.957	0.958	0.959	0.960	0.961	0.962	0.962	0.963
1.8	0.964	0.965	0.966	0.966	0.967	0.968	0.969	0.969	0.970	0.971
1.9	0.971	0.972	0.973	0.973	0.974	0.974	0.975	0.976	0.976	0.977
2.0	0.977	0.978	0.978	0.979	0.979	0.980	0.980	0.981	0.981	0.982
2.1	0.982	0.983	0.983	0.983	0.984	0.984	0.985	0.985	0.985	0.986
2.2	0.986	0.986	0.987	0.987	0.987	0.988	0.988	0.988	0.989	0.989
2.3	0.989	0.990	0.990	0.990	0.990	0.991	0.991	0.991	0.991	0.992
2.4	0.992	0.992	0.992	0.992	0.993	0.993	0.993	0.993	0.993	0.994
2.5	0.994	0.994	0.994	0.994	0.994	0.995	0.995	0.995	0.995	0.995
2.6	0.995	0.995	0.996	0.996	0.996	0.996	0.996	0.996	0.996	0.996
2.7	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997	0.997
2.8	0.997	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998
2.9	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.999	0.999	0.999

Quantiles of the Standard Normal Distribution

\(\alpha\)	\(\Phi^{-1}(\alpha)\)	\(\alpha\)	\(\Phi^{-1}(\alpha)\)	\(\alpha\)	\(\Phi^{-1}(\alpha)\)
0.01	-2.3263	0.34	-0.4125	0.67	0.4399
0.02	-2.0537	0.35	-0.3853	0.68	0.4677
0.03	-1.8808	0.36	-0.3585	0.69	0.4959
0.04	-1.7507	0.37	-0.3319	0.70	0.5244
0.05	-1.6449	0.38	-0.3055	0.71	0.5534
0.06	-1.5548	0.39	-0.2793	0.72	0.5828
0.07	-1.4758	0.40	-0.2533	0.73	0.6128
0.08	-1.4051	0.41	-0.2275	0.74	0.6433
0.09	-1.3408	0.42	-0.2019	0.75	0.6745
0.10	-1.2816	0.43	-0.1764	0.76	0.7063
0.11	-1.2265	0.44	-0.1510	0.77	0.7388
0.12	-1.1750	0.45	-0.1257	0.78	0.7722
0.13	-1.1264	0.46	-0.1004	0.79	0.8064
0.14	-1.0803	0.47	-0.0753	0.80	0.8416
0.15	-1.0364	0.48	-0.0502	0.81	0.8779
0.16	-0.9945	0.49	-0.0251	0.82	0.9154
0.17	-0.9542	0.50	0.0000	0.83	0.9542
0.18	-0.9154	0.51	0.0251	0.84	0.9945
0.19	-0.8779	0.52	0.0502	0.85	1.0364
0.20	-0.8416	0.53	0.0753	0.86	1.0803
0.21	-0.8064	0.54	0.1004	0.87	1.1264
0.22	-0.7722	0.55	0.1257	0.88	1.1750
0.23	-0.7388	0.56	0.1510	0.89	1.2265
0.24	-0.7063	0.57	0.1764	0.90	1.2816
0.25	-0.6745	0.58	0.2019	0.91	1.3408
0.26	-0.6433	0.59	0.2275	0.92	1.4051
0.27	-0.6128	0.60	0.2533	0.93	1.4758
0.28	-0.5828	0.61	0.2793	0.94	1.5548
0.29	-0.5534	0.62	0.3055	0.95	1.6449
0.30	-0.5244	0.63	0.3319	0.96	1.7507
0.31	-0.4959	0.64	0.3585	0.97	1.8808
0.32	-0.4677	0.65	0.3853	0.975	1.9600
0.33	-0.4399	0.66	0.4125	0.98	2.0537
				0.99	2.3263
				0.995	2.5758

5.5 The Binomial Distribution

5.5.1 Bernoulli Trials

At the beginning of this chapter, we introduced the central concept of a random experiment. We called any experiment a random experiment if it has at least two possible outcomes. This section of the chapter is dedicated to a special family of experiments that have exactly two outcomes, also known as Bernoulli trials¹. These are characterized by the following properties:

• The random experiment consists of trials with two alternative outcomes: success \(S\) and failure \(F\).

• The probability of success \(P(S)=p\) is called the probability of success, and \(P(F)=1-p\).

• The experiment is repeated \(n\) times.

• The repetitions are independent of each other and occur under the same conditions, so that \(p\) remains constant in all trials.

We are interested in the number of successes \(S_n\) in \(n\) experiments. Clearly, the random variable \(S_n\) can only take on the values \(0,1,\ldots,n\).

What is its probability distribution?

Example 5.72 (Stochastic Process Control)

In the context of quality control, samples of size \(n\) are drawn from ongoing production. The items in the sample are checked to see if they meet the quality requirements. \(S\) is the event that an inspected piece does not conform to the requirements. The probability \(p=P(S)\) is called the scrap rate of the process. \(S_n\) is the number of non-conforming items in a sample. If \(S_n\) is too large, then there is a justified suspicion that the production process is no longer under control.

Example 5.73 (Voting)

A committee consisting of \(n\) people votes in a secret ballot on a proposed project. Success \(S\) is the approval of a person, \(F\) is the rejection. \(S_n\) is the number of votes cast for the project. How probable is a majority for the project?

Example 5.74 (No-shows in Tourism)

An airplane with \(n\) seats is fully booked. The airline managers know from experience that a percentage \(p\) of passengers, known as no-shows, will not appear despite booking. If the probability distribution of \(S_n\), the number of no-shows, is known, the airline can strategically overbook to improve airplane occupancy.

5.5.2 Distribution of the Number of Successes

Theorem 5.75 (Binomial Distribution) The random variable \(S_n\), the number of successes in a series of \(n\) Bernoulli trials, follows a binomial distribution with: \[ \begin{gathered} P(S_n=k)=\binom{n}{k}p^k(1-p)^{n-k},\quad k=0,1,\ldots,n, \end{gathered} \tag{5.33}\] where \(\binom{n}{k}\) denotes the binomial coefficient: \[ \begin{gathered} \binom{n}{k}=\frac{n(n-1)(n-2)\cdots(n-k+1)}{k!}=\frac{n!}{k!(n-k)!}. \end{gathered} \] The expected value and variance of \(S_n\) are: \[ \begin{gathered} E(S_n)=np,\quad V(S_n)=np(1-p). \end{gathered} \tag{5.34}\]

Reasoning: If the event \(\{S_n=k\}\) occurs, there must be exactly \(k\) successes \(S\) and \(n-k\) failures \(F\) in the series of \(n\) experiments. Therefore, a series with a fixed arrangement of successes \(S\) has a probability of \(p^k(1-p)^{n-k}\), due to the independence of the experiments.

For example, let’s consider a sequence of experiments of length \(n=5\) with the outcomes (in the given order): \[ \begin{gathered} \mathit{SFFSF}\implies P(\mathit{SFFSF})=p^2(1-p)^3. \end{gathered} \] However, sequences like SSFFF, FFFSS, and seven other sequences also have the same probability \(p^2(1-p)^3\). Here, the binomial coefficient comes into play: \[ \begin{gathered} \binom{n}{k}=\begin{array}{l} \text{The number of ways to allocate places for the $k$ successes $S$}\\ \text{in a series of length $n$} \end{array} \end{gathered} \] This is easy to explain: a list of \(n\) objects can be arranged (permuted) in \[ \begin{gathered} n!=1\cdot 2\cdot 3\cdots n \end{gathered} \] different ways. However, our objects are of only two kinds, namely \(S\) and \(F\), and the \(S\) and \(F\) are not distinguishable from one another. This means that the \(k!\) permutations of the \(S\) all result in the same configuration, as are all \((n-k)!\) permutations of the failures \(F\) indistinguishable. Thus, the number of permutations is reduced by these two factors. Therefore, the number of ways to assign places to successes and failures in the experiment series is: \[ \begin{gathered} \frac{n!}{k!(n-k)!}=\binom{n}{k}, \end{gathered} \] thus proving (5.33). To find the expected value and variance, it is best to use indicator variables: \[ \begin{gathered} X_i=\left\{\begin{array}{cl} 1 & \text{if the $i$-th trial is a success $S$}\\[4pt] 0 & \text{if the $i$-th trial is a failure $F$} \end{array} \right.,\quad i=1,2,\ldots,n \end{gathered} \] Because of (5.20) for \(i=1,2,\ldots,n\); \[ \begin{gathered} E(X_i)=1\cdot p+0\cdot(1-p)=p,\quad E(X_i^2)=1^2\cdot p+0^2(1-p)=p, \end{gathered} \] and because of the shift theorem (Theorem 5.50): \[ \begin{gathered} V(X_i)=p-p^2=p(1-p). \end{gathered} \] Now, since \(S_n=X_1+X_2+\ldots+X_n\). Due to the linearity of the expected value (Theorem 5.40): \[ \begin{aligned} E(S_n)&=E(X_1+X_2+\ldots+X_n)\\ &=E(X_1)+E(X_2)+\ldots+E(X_n)\\ &=np. \end{aligned} \] And because the \(X_i\) are independent random variables, the addition theorem (Theorem 5.56) can be applied: \[ \begin{aligned} V(S_n)&=V(X_1+X_2+\ldots+X_n)\\ &=V(X_1)+\ldots+V(X_n)\\ &=np(1-p). \end{aligned} \] □

Figure 5.12 shows the probability function (5.33) of the binomial distribution for \(n=10\) and various values of the success probability \(p\).

Figure 5.12: Binomial distribution for \(n=10\) and various \(p\).

Exercise 5.76 (Statistical Process Control) A production process is considered under control if it operates with a defective rate of a maximum of 1.5%. To verify this, a sample of size \(n=10\) is drawn from the ongoing production and the selected items are checked for compliance with the quality standards. It was found that two inspected items did not meet the standards.

How likely is it to find at least two unusable items in the sample if the process is under control?

Solution: We define success \(S\) as the event {inspected item does not meet the standards}. If the process is under control, then the probability of success is \(p=0.015\). Let \(S_{10}\) be the number of unusable items in a sample of size \(n=10\).

We are looking for \(P(S_{10}\ge 2)\). Using (5.33): \[ \begin{aligned} &P(S_{10}\ge 2)\\ &=1 - P(S_{10}\le 1)\\[4pt] &=1-\left[P(S_{10}=0)+P(S_{10}=1)\right]\\[4pt] &=1-\left[\binom{10}{0}0.015^0(1-0.015)^{10}+\binom{10}{1}0.015^1(1-0.015)^{9}\right]\\[4pt] &=1-\left[0.85973 + 0.13092\right]=0.00935\,. \end{aligned} \] Therefore, it is very unlikely to find two or more defective items in a 10-item sample if the process is running with a defect rate of 1.5%. This result is thus strong evidence that the hypothesis \(p=0.015\) can no longer be upheld. □

Exercise 5.77 (Voting Behavior) The five-member board of an association must vote on a motion from an association member at short notice.

1. If the board members are completely indifferent and undecided (probability of approval \(p=0.5\)), what is the probability that the motion wins a majority?

2. Four of the board members are indifferent (\(p=0.5\)), but one member of the board is definitely against the motion. How likely is it now that the motion will be approved by a majority?

It is assumed that the vote is secret and therefore independence is ensured.

Solution:

(a) Let \(S_5\) be the number of votes in favor of the motion. It is approved by a majority if \(S_5\ge 3\): \[ \begin{aligned} P(S_5\ge 3)&=P(S_5=3)+P(S_5=4)+P(S_5=5)\\[5pt] &=\binom{5}{3}0.5^5+\binom{5}{4}0.5^5+\binom{5}{5}0.5^5\\[5pt] &=0.312500 + 0.156250 + 0.031250 = 0.5\,. \end{aligned} \] As expected, the motion has a fifty-fifty chance of being approved.

(b) Since one is definitely against the motion, at least three of the remaining four must vote in favor: \[ \begin{aligned} P(S_4\ge 3)&=P(S_4=3)+P(S_4=4)\\[5pt] &=\binom{4}{3}0.5^4+\binom{4}{4}0.5^4=0.25+0.0625=0.3125\,. \end{aligned} \] The chances of the motion are now significantly lower. □

Exercise 5.78 The intelligence quotient is normally distributed with \(\mu=100\) and \(\sigma=15\). A child is considered to be gifted if it scores an IQ of over 130 in a test. A class of 20 children is tested. How likely is it to find more than one gifted child in this class?

Solution: First we calculate the probability that the intelligence quotient \(Q>130\) is: \[ \begin{aligned} P(Q>130)&=1-P(Q\le130)\\ &=1-\Phi\left(\frac{130-100}{15}\right)=1-\Phi(2)=0.023\,. \end{aligned} \] Now, one child in the class can be gifted (success) with probability \(0.023\), or they are not gifted. Assuming independence, the number of gifted children in the class is binomially distributed with \(n=20\) and \(p=0.023\). We are looking for \(P(S_{20}>1)\): \[ \begin{aligned} P(S_{20}>1)&=1-P(S_{20}\le 1)\\[5pt] &=1-\left[P(S_{20}=0)+P(S_{20}=1)\right]\\[5pt] &=1-\left[\binom{20}{0}0.023^0\cdot 0.977^{20}+\binom{20}{1}0.023^1\cdot 0.977^{19}\right]\\[5pt] &=1-[0.62790 + 0.29563]=0.07647\,. \end{aligned} \] □

5.5.3 Approximation by the Normal Distribution

Calculating probabilities of the binomial distribution can often be very cumbersome, especially because the binomial coefficients become extremely large numbers, even for moderate values of \(n\). However, since the random variable \(S_n\) can be expressed as the sum of independent random variables (see formulas at Figure 5.12), one can use the central limit theorem, i.e. an approximation by the normal distribution.

More precisely: we approximate the distribution function of \(S_n\), i.e. the probability \(P(S_n\le k)\), by the distribution function of a random variable \(X\), which is normally distributed with mean and variance as we have found in Theorem 5.75, namely: \[ \begin{gathered} \mu=np,\quad \sigma^2=np(1-p). \end{gathered} \] To increase accuracy, it is appropriate to add a continuity correction of \(0.5\) to \(k\), so that: \[ \begin{gathered} P(S_n\le k)\approx P(X\le k+0.5)=\Phi\left(\frac{k+0.5-\mu}{\sigma}\right). \end{gathered} \tag{5.35}\] This approximation usually yields reasonably accurate values when the variance \(\sigma^2>9\).

Exercise 5.79 An airline frequently uses the A320-200 model for many of its routes, which has a seating capacity of 180 passengers. Experience has shown that 7.5% of the passengers do not show up for the flight despite having valid tickets, known as no-shows.

1. How likely is it that there are more than 10 seats left unoccupied in a fully booked plane?

2. How many seats can the flight be overbooked by such that there’s a 99% probability that no passenger with a valid ticket will be turned away?

Solution:

(a) The number \(S_n\) of no-shows among \(n\) bookings follows a binomial distribution with \(p=0.075\). For \(n=180\), we first calculate: \[ \begin{gathered} \mu=180\cdot 0.075=13.5,\quad \sigma^2=180\cdot 0.075\cdot0.925=12.4875>9. \end{gathered} \] Since the variance \(\sigma^2>9\) we expect an approximation of acceptable accuracy: \[ \begin{aligned} P(S_{180}>10)&=1-P(S_{180}\le 10)\approx 1-\Phi\left(\frac{10+0.5-13.5}{\sqrt{12.4875}} \right)\\[5pt] &=1-\Phi(-0.85)=1-0.198=0.802\,. \end{aligned} \] The exact value of this probability, calculated with a computer program, is \(P(S_{180}>10)=0.79911\). The approximation error is only 0.0029!

(b) Let \(m\) be the number of tickets sold beyond the limit of 180. The total number of bookings is then \(N=180+m\). Again, let \(S_N\) be the number of no-shows. The event {no passenger has to be turned away} can only occur if \(S_N \ge m\), because then the number of no-shows is at least as large as the number of overbookings. This \(S_N\) is approximately normally distributed with expectation value \[ \begin{gathered} \mu=Np=(180+m)\cdot 0.075=13.5+0.075m \end{gathered} \] and variance \[ \begin{aligned} \sigma^2&=Np(1-p)=(180+m)\cdot 0.075\cdot(1-0.075)\\[5pt] &=12.487500 + 0.069375 m. \end{aligned} \] Now we formulate an equation for the unknown \(m\) from the requirement \(P(S_N \ge m)=0.99\): \[ \begin{gathered} P(S_N\ge m)=1-P(S_N\le m-1)=0.99\\[5pt] \implies P(S_N\le m-1)=0.01\,. \end{gathered} \] Next the approximation using the central limit theorem: \[ \begin{gathered} P(S_N\le m-1)\approx\Phi\left(\frac{m-1+0.5-(13.5+0.075m)}{ \sqrt{12.4875 + 0.069375 m}}\right)=0.01\\[5pt] \frac{0.925 m - 14}{\sqrt{12.4875 + 0.069375\, m}}=\Phi^{-1}(0.01)=-2.3263\\[5pt] 0.925 m - 14=-2.3263\sqrt{12.4875 + 0.069375\, m}\,. \end{gathered} \] To eliminate the square root, we square both sides of the equation, but we must remember that squaring is not an equivalent transformation. Indeed, we obtain (after simplification) the quadratic equation: \[ \begin{gathered} 0.855625 \,m^2 - 26.27543472\, m + 128.4217498=0. \end{gathered} \] It has two solutions: \[ \begin{gathered} m_1=6.10\simeq 6,\quad m_2=24.61\simeq 25. \end{gathered} \] We take the solution \(m=6\) and thus we accept \(N=186\) bookings.

You can easily verify that with \(N=180+25=205\) bookings, there is a 99% probability that at least one passenger would have to be turned away. □

5.6 Additional Exercises

1. A gambler participates in a fair game of chance. Let \(W\) be the waiting time (number of individual games) until the first win. Calculate \(P(3<W\le 8)\).

   Solution: \(P(3<W\le 8)=P(S_3=0)-P(S_8=0)=0.1211\)

2. A die is thrown four times, how likely is it to roll at least one six? Two dice are thrown 24 times, how likely is it to roll at least one double six?

   Solution: \(0.5177>0.4914\), De Méré’s Paradox (1654)

3. A family has two children. It is known that one of them is a girl. What is the probability that both children are girls?

   Solution: \(1/3\)

4. Surveys have shown that 40 percent of television viewers regularly watch the news program ZIB 2 and 80 percent watch ZIB 1. 90 percent of viewers watch at least one of the two programs. What is the probability that a randomly selected viewer watches both programs?

   Solution: 0.3

5. In a technical study, the following events were recorded for cars: \(R=\) {The car has rust damage} and \(S=\) {The car is maintained with the brand product XY}. It turns out that \(P(R) = 0.37\) and \(P(S) = 0.71\). Also, \(P(R \cap S) = 0.11\).

   1. Determine the probability that a vehicle maintained with XY has rust damage.

   2. Determine the probability that a vehicle with rust damage is maintained with XY.

   3. Determine the probability that a vehicle without rust damage is maintained with XY.

   4. Determine the probability that a vehicle with rust damage is not maintained with XY.

   Solution:

   (a) \(P(R|S)=0.1549\), (b) \(P(S|R)=0.2973\), (c) \(P(S|R')=0.9524\)
   (d) \(P(S'|R)=0.7027\)

6. A survey revealed that 18 percent of all male students smoke. 42 percent of all students smoke. 68 percent of all non-smoking students are female.

   1. What is the probability that a female student smokes?

   2. What is the probability that a male student does not smoke?

   Solution: (a) \(P(R|W)=0.3783\), (b) \(P(R'|M)=0.5077\)

7. In 2010, 19 out of the 28 EU countries were part of the Euro. Of these, only four complied with the Maastricht Treaty’s deficit limit of 3% of GDP. Of the 9 EU countries not in the Eurozone, 7 did not comply with the deficit limit.

   1. What percentage of Euro countries were Maastricht offenders?

   2. What percentage of Maastricht offenders were Euro countries?

3. How do you assess the coupling between the characteristics \(E=\) {Member of the Eurozone} and \(M=\) {Adherence to the 3% limit}?

Solution: (a) \(P(M'|E)=0.7895\), (b) \(P(E|M')=0.6818\), (c) \(E\) and \(M\) are practically independent.

8. In a company, there are 40 women and 75 men employed. 62 employees have a university degree, of which 25 are female.

Which of the following statements are true?

1. 26.1% of the employees are female and have a university degree.

2. 37.5% of the women do not have a university degree.

3. 40.3% of the employees with a university degree are female.

Solution: Statements (2) and (3) are correct.

9. For two events \(A\) and \(B\), which can be observed in an experiment, the following contingency table was determined: \[ \begin{gathered} \begin{array}{l|cc|r} & A & A' &\\ \hline B & 0.40 & 0.10 & 0.50\\ B' & 0.20 & 0.30 & 0.50\\ \hline & 0.60 & 0.40 & \end{array} \end{gathered} \] Which of the following statements are true?

1. \(P(A\cap B)=0.40\)

2. \(P(A'|B)=0.25\)

3. \(P(A'|B')=0.60\)

Solution: Statements (1) and (3) are correct.

10. In Europe, 9% of men have red-green color blindness, but only 0.8% of women. What is the proportion of women among people with red-green color blindness (population proportion of women: 50%)?

Solution: 8.2%

11. A discrete random variable \(X\) has the following probability function: \[ \begin{gathered} \begin{array}{c|ccccc} X & 0 & 1 & 2 & 3 & 4\\ \hline P(X=x) & 0.1 & 0.1 & 0.4 & 0.3 & 0.1 \end{array} \end{gathered} \] Calculate the expected value and variance of \(X\).

Solution: \(\mu = 2.2, \sigma^2= 1.16\)

12. A company produces with a linear cost function. The variable costs are 17 monetary units (MU) per unit, the fixed costs are one million MU per month. The monthly production quantity \(X\) is a random variable with an expected value of 21,000 units. The market price \(P\) that can be achieved is also a random variable, independent of \(X\), with \(E(P)=80\) MU. Calculate the expected monthly profit, assuming that the entire production can be sold.

Solution: \(323,000\)

13. An investor creates a portfolio including four securities \(A,B,C,D\) with capital shares of 25%, 40%, 10%, and 25%, respectively. The yields of these securities are independent random variables.From these four papers, she knows the expected returns and the standard deviations of the returns. \[ \begin{gathered} \begin{array}{c|cccc} & A & B & C & D\\ \hline E(R_i) & 0.08 & 0.12 & 0.06 & 0.09\\ \sigma(R_i) & 0.06 & 0.09 & 0.01 & 0.08 \end{array} \end{gathered} \] Calculate the expected combined return of the portfolio and its standard deviation.

Solution: \(E(R)=0.0965\), \(\sigma(R)=0.0438\)

14. An investor wants to create a portfolio that guarantees him minimal risk. 10% of the capital is to be invested risk-free in security \(C\), which contractually guarantees a return of 6%. The remaining capital should be optimally distributed between two securities \(A\) and \(B\). The following data are available: \[ \begin{gathered} \begin{array}{c|ccc} & A & B & C\\ \hline E(R_i) & 0.14 & 0.16 & 0.06\\ \sigma(R_i) & 0.08 & 0.09 & 0.00 \end{array} \end{gathered} \] The returns of \(A\) and \(B\) are independent random variables. What are the capital shares of \(A\) and \(B\) in the optimal portfolio, and what is the expected combined return?

Solution: Share \(A\): 50.3%, Share \(B\): 39.7%, \(E(R)=0.14\).

15. A trading company produces packages of coffee beans with an expected weight of \(\mu=250\) \(g\) and a standard deviation of \(\sigma=16\) \(g\). During quality control, boxes with 8 packages each are weighed. What are the expected value and standard deviation of the average weight of a package in a box?

Solution: \(E(\overline{X})=E(X)=250\), \(\sigma(\overline{X})=\sqrt{32}=5.6569\)

16. The gasoline consumption of cars (in liters, per 100 km) is normally distributed with a mean of 8.2 and a variance of 2.4.

1. What percentage of cars consume more than 10 liters?

2. Which consumption is exceeded by 25 percent of the cars?

Solution: (a) \(P(X>10)=0.123\), (b) 9.24 Liters/100 km.

17. The operating time of a device until the first failure (in months) is normally distributed with \(\mu = 24.15\) and \(\sigma^2 = 121\). A dealer guarantees to replace the device if it fails within the first 6 months. How many warranty cases are to be expected for 6000 devices?

Solution: 294

18. In an accident-prone section of the highway, extensive radar measurements of speeds were carried out. It was found that the driving speeds are approximately normally distributed with a mean of 95 km/h and a standard deviation of 12 km/h. For traffic safety reasons, there is a speed limit of 100 km/h on the stretch. What is the proportion of vehicles that exceed the speed limit? What speed is exceeded by 1% of the vehicles?

Solution: \(0.337\), \(123\) km/h

19. The Prepackaged Goods Regulation 1993 (FPVO) specifies in § (1) that for containers with a nominal fill volume of 500 milliliters, the deviation from this value may be a maximum of \(\pm\) 2% of the volume. Assuming the fill volumes of a bottling plant are normally distributed with an expected value of 500 ml and a standard deviation of 3.8 ml. With what probability are the specifications of the FPVO adhered to?

    Solution: \(0.992\)

20. A queue has formed in front of the cash register of a cinema, Mr. A is in 21st place. The time it takes for a visitor at the cash register to buy their ticket is a random variable with an expected value of 63 seconds and a standard deviation of 60 seconds. The waiting time for A is the sum of the service times of all visitors in front of him in the queue. How likely is it that A will wait more than half an hour? Approximate this probability using the central limit theorem.

    Solution: \(0.022\)

21. A commercial aircraft has four engines. The probability that an engine will fail or needs to be shut down due to technical problems during a transatlantic flight is \(0.001\). How likely is it that two or more engines will fail during a transatlantic flight?

    Solution: \(0.000005992\)

22. The probability of a major accident occurring during a technical operation is 1:10,000 over the span of a year. What is the probability that when operating 30 facilities over the course of 10 years, the accident occurs at least once?

    Solution: \(0.0296\)

23. A banking company knows that 18 percent of private borrowers choose to overdraw their salary account as a form of financing, although an interest of 13% per year is charged for this. What is the probability that at least one of 8 randomly selected customers will overdraw their salary account?

    Solution: \(0.7956\)

24. A Viennese family is building their weekend house in a romantic location on a river. The river was once regulated s that it would overflow its banks within a year with a probability of 0.06.

    1. How likely is it to experience exactly 3 years with floods in the next 20 years.

    2. How likely is it to experience at most 3 years with floods in the next 20 years.

    Solution: (a) \(0.086\), (b) \(0.971\)

25. The party The Greens achieved a vote share of 3.8% in the National Council election of 2017. As part of an analysis after the election, a random sample is drawn. How large must the sample size be so that with a confidence of 99%, it contains at least one voter of The Greens?

    Solution: \(n\ge 119\)

26. The service time \(T\) (scanning of items, payment process) of a customer at a supermarket checkout is exponentially distributed with \(P(T>t)=e^{-0.0125t}\) (time in seconds). How likely is it that out of 10 randomly selected customers, no more than three spend longer than two minutes at the checkout?

    Solution: \(0.835\)

27. A production process runs under ideal conditions with a defect rate of 2.2%. For purposes of quality control, samples of the size \(n=20\) are taken from the ongoing production at certain time intervals and the products are checked for their quality. The forewoman is instructed to stop the process if more than two of the 20 controlled items are defective.

    1. How likely is it that the process is stopped when the machine is working with a defect rate of 2.2%?

    2. How likely is this event if a disturbance has actually increased the defect rate to 8%?

    Solution: (a) \(0.0092\), (b) \(0.2121\)

---

1. Jacob I. Bernoulli (1655–1705), a Swiss mathematician and physicist with significant contributions to probability theory. He formulated an early version of the Law of Large Numbers.